如果你也在 怎样代写数据可视化Intro to Data Analytics & Visualization这个学科遇到相关的难题,请随时右上角联系我们的24/7代写客服。数据可视化Intro to Data Analytics & Visualization数据可视化是以图画或图形的形式表示信息和数据(例如:图表、图形和地图)。数据可视化工具提供了一种方便的方式来查看和理解数据中的趋势、模式和异常值。数据可视化工具和技术对于分析海量信息和做出数据驱动的决策至关重要。使用图片来理解数据的概念自几个世纪以来一直被使用。数据可视化的一般类型是图表、表格、图形、地图、仪表盘。
数据可视化Intro to Data Analytics & Visualization析是分析数据集的过程,以便对他们所拥有的信息做出决策,越来越多地使用专门的软件和系统。数据分析技术被用于商业行业,使组织能够做出商业决策。数据可以帮助企业更好地了解他们的客户,改善他们的广告活动,个性化他们的内容,并提高他们的底线。数据分析的技术和过程已经被自动化为机械过程和算法,在原始数据上工作,供人使用。数据分析帮助企业优化其业绩。
my-assignmentexpert™ 数据可视化Intro to Data Analytics & Visualization作业代写,免费提交作业要求, 满意后付款,成绩80\%以下全额退款,安全省心无顾虑。专业硕 博写手团队,所有订单可靠准时,保证 100% 原创。my-assignmentexpert™, 最高质量的数据可视化Intro to Data Analytics & Visualization作业代写,服务覆盖北美、欧洲、澳洲等 国家。 在代写价格方面,考虑到同学们的经济条件,在保障代写质量的前提下,我们为客户提供最合理的价格。 由于统计Statistics作业种类很多,同时其中的大部分作业在字数上都没有具体要求,因此数据可视化Intro to Data Analytics & Visualization作业代写的价格不固定。通常在经济学专家查看完作业要求之后会给出报价。作业难度和截止日期对价格也有很大的影响。
想知道您作业确定的价格吗? 免费下单以相关学科的专家能了解具体的要求之后在1-3个小时就提出价格。专家的 报价比上列的价格能便宜好几倍。
my-assignmentexpert™ 为您的留学生涯保驾护航 在data analysis作业代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的data analysis代写服务。我们的专家在数据可视化Intro to Data Analytics & Visualization代写方面经验极为丰富,各种数据可视化Intro to Data Analytics & Visualization相关的作业也就用不着 说。
我们提供的数据可视化Intro to Data Analytics & Visualization及其相关学科的代写,服务范围广, 其中包括但不限于:

data analysis代写|数据可视化代写Intro to Data Analytics & Visualization代考|Distance measures
Partitioning clustering algorithms iteratively define $k$ cluster centers and assign cluster membership (or the probability of group membership) to cases based on distances between the case and the cluster. Agglomerative clustering algorithms also create clusters based on distances, starting with each individual belonging to a separate cluster and the grouping clusters two by two. The k-nearest neighbors algorithm also uses distance measures.
Consider only one attribute, for instance the height of individuals. The distance of someone measuring $180 \mathrm{~cm}$ and someone measuring $170 \mathrm{~cm}$ will be 10 on this sole dimension considering the algebraic difference between the two measures as our distance metric. Things get a little more complicated when we add more attributes, such as weight (we will not consider variable scaling here). Let’s say the first individual is clearly overweight $(90 \mathrm{~kg})$, and the second has a normal weight $(80 \mathrm{~kg})$. Considering only the sum of the difference between the measures as our distance metric, the difference between the individuals would be: $(180-170)+(90-100)=0$. This clearly doesn’t reflect the huge differences between these individuals; one is bigger and slimmer than the other. Several distance metrics are available. Here are some examples:
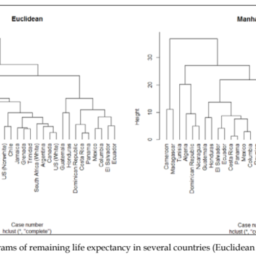
The metrics closest to the sum of differences measure we just examined are the Euclidean and the Manhattan distances.
The Manhattan distance sums the absolute value of the differences on all considered dimensions. Its mathematical equation is provided next:
$$
\sum_{i=1}^{n}\left|p_{i}-q_{i}\right|
$$
Take the case of our previous example, $a b s(180-170)+a b s(90-100)=20$. For one dimension, it is equivalent to the difference between two observations: abs(180-170) $=180-170=10$. The Manhattan distance can be selected in hclust ( ), which we will discover later, but not in kmeans ().
The Euclidean distance sums the squares of the differences and then performs a square root on the result. In case of only one dimension, the result is equal to the difference between observations. Its mathematical equation is provided below:
$$
\sqrt{\left(\sum_{i=1}^{n} p_{i}-q_{i}\right)^{2}}
$$
data analysis代写|数据可视化代写Intro to Data Analytics & Visualization代考|Setting the centroids
First, we need a function that attributes membership to the clusters randomly. We do this for all the observations at the same time, and return the result as vector clusters (see line 2). Our function takes 2 arguments: the number of observations (numrows) and the number of clusters ( $k$ ).
1 set. random, clusters = function (numrows, $k$ ) {
clusters = sample $(1: k$, numrows, replace=T $)$
}
We then create a function that computes the centroids – that is, the means for each case on each dimension and each cluster. Our function takes 2 arguments: the data frame on which to cluster the data (df), and the current cluster assignments (clusters).
1 compute.centroids = function (df, clusters) {
means = tapply (df $[, 1]$, clusters, mean)
for (i in $2: \operatorname{ncol}(d f)$ ) {
mean. case $=\operatorname{tapply}(\mathrm{df}[, i]$, clusters, mean $)$
means $=$ rbind (means, mean. case)
}
centroids $=$ data frame (t(means))
names (centroids) = names (df)
centroids
}
On line 2, we assign to vector means the mean values of attribute in column 1 for each of the clusters. In a loop, we assign to vector mean. case the values of attribute in column i for each cluster, and append it to means (lines 4 and 5). We then make a data frame from the transpose of object means and assign it to object centroids (line
8) We name the columns of this object as the columns in the original data frame (line
9). Finally we return centroids (line 9).
DATA ANALYSIS代写|数据可视化代写INTRO TO DATA ANALYTICS & VISUALIZATION代考|Tasks performed by the main function
We now almost have everything we need for our basic k-means implementation. We finally need to wrap this together in a main function, which we call kay .means (). Here we set initial cluster value (line 2) and then iterate over the computation of centroids (line 7), the calculation of distances (line 8), and the re-assignment of clusters (line 11). Notice the code block is contained in a while loop, which stops when the sum of squares of the distances (that is the total sum of squares within clusters) is the same twice in a row (when ss . old equal to ss – this value is set on line 10), and output the clustering solution (line 14).
Let’s try this using a very popular dataset, which we have already encountered in the previous chapter: the iris dataset, where observations are 150 iris flowers. Attributes are the species of the flowers and their petal and sepal length and width. So, in this case, we know the groups beforehand and are interested in knowing whether k-means can predict it from the other attributes. Let’s start by having a look at the correct classification, which is in the 5 th column of the data set.
iris [5]
We will not display the full output here, but you will see in your console that cases 1 to 50 are of species Setosa, cases 51 to 100 are of species Versicolor, and cases 101 to 150 of species Virginica.
We will use our knowledge of the dataset to determine the number of clusters. We select three clusters as we know there are three species. We will talk later about determining the number of clusters when this information is not available.
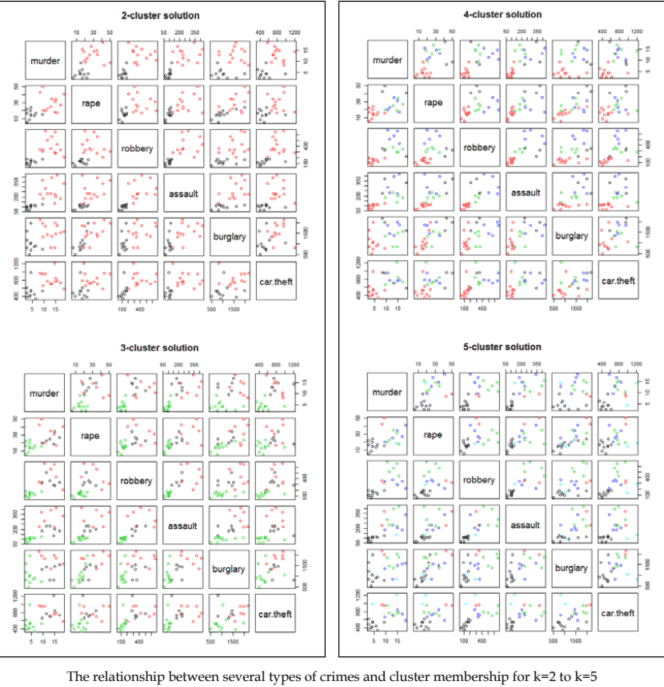
数据可视化代写
DATA ANALYSIS代写|数据可视化代写INTRO TO DATA ANALYTICS & VISUALIZATION代考|DISTANCE MEASURES
分区聚类算法迭代定义ķ集群中心并分配集群成员这r吨H和pr这b一种b一世l一世吨是这FGr这在p米和米b和rsH一世p基于案例和集群之间的距离来区分案例。凝聚聚类算法还根据距离创建聚类,从属于单独聚类的每个个体开始,然后将聚类两两分组。k-最近邻算法也使用距离度量。
只考虑一个属性,例如个人的身高。某人测量的距离180 C米和有人测量170 C米考虑到两个度量之间的代数差异作为我们的距离度量,在这个唯一维度上将是 10。当我们添加更多属性时,事情会变得有点复杂,比如重量在和在一世lln这吨C这ns一世d和r在一种r一世一种bl和sC一种l一世nGH和r和. 假设第一个人明显超重(90 ķG), 第二个有正常的重量(80 ķG). 仅考虑作为我们的距离度量的度量之间差异的总和,个体之间的差异将是:(180−170)+(90−100)=0. 这显然没有反映出这些人之间的巨大差异。一个比另一个更大更苗条。有几个距离度量可用。以下是一些示例:
最接近我们刚刚检查的差异总和的度量是欧几里得距离和曼哈顿距离。
曼哈顿距离对所有考虑的维度上的差异的绝对值求和。其数学方程如下:
∑一世=1n|p一世−q一世|
以我们之前的例子为例,一种bs(180−170)+一种bs(90−100)=20. 对于一维,它相当于两个观察值之间的差异:abs180−170 =180−170=10. 曼哈顿距离可以在hclust中选择,我们稍后会发现,但不是在 kmeans 中.
欧几里得距离对差的平方求和,然后对结果进行平方根。在只有一维的情况下,结果等于观测值之间的差异。其数学方程如下:
$$
\sqrt{\left(\sum_{i=1}^{n} p_{i}-q_{i}\right)^{2}}
$$
DATA ANALYSIS代写|数据可视化代写INTRO TO DATA ANALYTICS & VISUALIZATION代考|SETTING THE CENTROIDS
首先,我们需要一个将成员资格随机分配给集群的函数。我们同时对所有观察结果执行此操作,并将结果作为向量簇返回s和和l一世n和2. 我们的函数有 2 个参数:观察次数n在米r这在s和集群的数量$ķ$.
1套。随机,簇 = 函数n在米r这在s,$ķ${
集群 = 样本(1:ķ, numrows, 替换=T)
然后
我们创建一个计算质心的函数——即每个维度和每个集群上每个案例的均值。我们的函数有 2 个参数:用于对数据进行聚类的数据框dF,以及当前的集群分配Cl在s吨和rs.
1 compute.centroids = function (df, clusters) {
means = tapply (df $[, 1]$, clusters, mean)
for (i in $2: \operatorname{ncol}(d f)$ ) {
mean. case $=\operatorname{tapply}(\mathrm{df}[, i]$, clusters, mean $)$
means $=$ rbind (means, mean. case)
}
centroids $=$ data frame (t(means))
names (centroids) = names (df)
centroids
}
在第 2 行,我们将向量分配给每个集群的第 1 列中属性的平均值。在一个循环中,我们分配给向量均值。每个集群的第 i 列中的属性值的大小写,并将其附加到均值l一世n和s4一种nd5. 然后,我们从对象均值的转置中创建一个数据框,并将其分配给对象质心l一世n和8我们将此对象的列命名为原始数据框中的列l一世n和9. 最后我们返回质心l一世n和9.
DATA ANALYSIS代写|数据可视化代写INTRO TO DATA ANALYTICS & VISUALIZATION代考|TASKS PERFORMED BY THE MAIN FUNCTION
现在,我们几乎拥有了基本 k-means 实现所需的一切。我们最终需要将其包装在一个主函数中,我们称之为 kay .means. 这里我们设置初始集群值l一世n和2然后迭代质心的计算l一世n和7, 距离的计算l一世n和8,以及集群的重新分配l一世n和11. 注意代码块包含在一个while循环中,当距离的平方和时停止吨H一种吨一世s吨H和吨这吨一种ls在米这Fsq在一种r和s在一世吨H一世nCl在s吨和rs连续两次相同在H和nss.这ld和q在一种l吨这ss–吨H一世s在一种l在和一世ss和吨这nl一世n和10,并输出聚类解l一世n和14.
让我们使用一个非常流行的数据集来试试这个,我们在上一章中已经遇到过:鸢尾花数据集,其中观察到 150 朵鸢尾花。属性是花的种类及其花瓣和萼片的长度和宽度。因此,在这种情况下,我们事先知道这些组,并且有兴趣知道 k-means 是否可以从其他属性中预测它。让我们先看看正确的分类,它位于数据集的第 5 列。
虹膜5
我们不会在此处显示完整输出,但您会在控制台中看到案例 1 到 50 属于 Setosa 物种,案例 51 到 100 属于 Versicolor 物种,案例 101 到 150 属于 Virginica 物种。
我们将使用我们对数据集的了解来确定集群的数量。我们选择三个集群,因为我们知道有三个物种。我们稍后将讨论在无法获得此信息时确定集群的数量。

data analysis代写|数据可视化代写Intro to Data Analytics & Visualization代考 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。
电磁学代考
物理代考服务:
物理Physics考试代考、留学生物理online exam代考、电磁学代考、热力学代考、相对论代考、电动力学代考、电磁学代考、分析力学代考、澳洲物理代考、北美物理考试代考、美国留学生物理final exam代考、加拿大物理midterm代考、澳洲物理online exam代考、英国物理online quiz代考等。
光学代考
光学(Optics),是物理学的分支,主要是研究光的现象、性质与应用,包括光与物质之间的相互作用、光学仪器的制作。光学通常研究红外线、紫外线及可见光的物理行为。因为光是电磁波,其它形式的电磁辐射,例如X射线、微波、电磁辐射及无线电波等等也具有类似光的特性。
大多数常见的光学现象都可以用经典电动力学理论来说明。但是,通常这全套理论很难实际应用,必需先假定简单模型。几何光学的模型最为容易使用。
相对论代考
上至高压线,下至发电机,只要用到电的地方就有相对论效应存在!相对论是关于时空和引力的理论,主要由爱因斯坦创立,相对论的提出给物理学带来了革命性的变化,被誉为现代物理性最伟大的基础理论。
流体力学代考
流体力学是力学的一个分支。 主要研究在各种力的作用下流体本身的状态,以及流体和固体壁面、流体和流体之间、流体与其他运动形态之间的相互作用的力学分支。
随机过程代写
随机过程,是依赖于参数的一组随机变量的全体,参数通常是时间。 随机变量是随机现象的数量表现,其取值随着偶然因素的影响而改变。 例如,某商店在从时间t0到时间tK这段时间内接待顾客的人数,就是依赖于时间t的一组随机变量,即随机过程
Matlab代写
MATLAB 是一种用于技术计算的高性能语言。它将计算、可视化和编程集成在一个易于使用的环境中,其中问题和解决方案以熟悉的数学符号表示。典型用途包括:数学和计算算法开发建模、仿真和原型制作数据分析、探索和可视化科学和工程图形应用程序开发,包括图形用户界面构建MATLAB 是一个交互式系统,其基本数据元素是一个不需要维度的数组。这使您可以解决许多技术计算问题,尤其是那些具有矩阵和向量公式的问题,而只需用 C 或 Fortran 等标量非交互式语言编写程序所需的时间的一小部分。MATLAB 名称代表矩阵实验室。MATLAB 最初的编写目的是提供对由 LINPACK 和 EISPACK 项目开发的矩阵软件的轻松访问,这两个项目共同代表了矩阵计算软件的最新技术。MATLAB 经过多年的发展,得到了许多用户的投入。在大学环境中,它是数学、工程和科学入门和高级课程的标准教学工具。在工业领域,MATLAB 是高效研究、开发和分析的首选工具。MATLAB 具有一系列称为工具箱的特定于应用程序的解决方案。对于大多数 MATLAB 用户来说非常重要,工具箱允许您学习和应用专业技术。工具箱是 MATLAB 函数(M 文件)的综合集合,可扩展 MATLAB 环境以解决特定类别的问题。可用工具箱的领域包括信号处理、控制系统、神经网络、模糊逻辑、小波、仿真等。