如果你也在 怎样代写微积分Calculus 这个学科遇到相关的难题,请随时右上角联系我们的24/7代写客服。微积分Calculus 最初被称为无穷小微积分或 “无穷小的微积分”,是对连续变化的数学研究,就像几何学是对形状的研究,而代数是对算术运算的概括研究一样。
微积分Calculus 它有两个主要分支,微分和积分;微分涉及瞬时变化率和曲线的斜率,而积分涉及数量的累积,以及曲线下或曲线之间的面积。这两个分支通过微积分的基本定理相互关联,它们利用了无限序列和无限数列收敛到一个明确定义的极限的基本概念 。17世纪末,牛顿(Isaac Newton)和莱布尼兹(Gottfried Wilhelm Leibniz)独立开发了无限小数微积分。后来的工作,包括对极限概念的编纂,将这些发展置于更坚实的概念基础上。今天,微积分在科学、工程和社会科学中得到了广泛的应用。
微积分Calculus 代写,免费提交作业要求, 满意后付款,成绩80\%以下全额退款,安全省心无顾虑。专业硕 博写手团队,所有订单可靠准时,保证 100% 原创。 最高质量的微积分Calculus 作业代写,服务覆盖北美、欧洲、澳洲等 国家。 在代写价格方面,考虑到同学们的经济条件,在保障代写质量的前提下,我们为客户提供最合理的价格。 由于作业种类很多,同时其中的大部分作业在字数上都没有具体要求,因此微积分Calculus 作业代写的价格不固定。通常在专家查看完作业要求之后会给出报价。作业难度和截止日期对价格也有很大的影响。
同学们在留学期间,都对各式各样的作业考试很是头疼,如果你无从下手,不如考虑my-assignmentexpert™!
my-assignmentexpert™提供最专业的一站式服务:Essay代写,Dissertation代写,Assignment代写,Paper代写,Proposal代写,Proposal代写,Literature Review代写,Online Course,Exam代考等等。my-assignmentexpert™专注为留学生提供Essay代写服务,拥有各个专业的博硕教师团队帮您代写,免费修改及辅导,保证成果完成的效率和质量。同时有多家检测平台帐号,包括Turnitin高级账户,检测论文不会留痕,写好后检测修改,放心可靠,经得起任何考验!
想知道您作业确定的价格吗? 免费下单以相关学科的专家能了解具体的要求之后在1-3个小时就提出价格。专家的 报价比上列的价格能便宜好几倍。
我们在数学Mathematics代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的数学Mathematics代写服务。我们的专家在微积分Calculus Assignment代写方面经验极为丰富,各种微积分Calculus Assignment相关的作业也就用不着 说。
数学代写|微积分代写Calculus代考|Graffkler ve Doğrular
Bu bölümde, en temel geometrik şekillerden biri olan doğruyu inceleyeceğiz. Bu kitapta dŏ̆ru kavramm kullandığımızda geometrideki anlamıyla düz doğruyu kastedeceğiz. Bir doğruyu tanmayı, grafiğini çizmeyi ve doğrunun denklemini bulabilmek için doğru ile ilgili bilgilerin nasıl kullanılacağın öğreneceğiz. Bir denklemin grafiğinin incelenmesi, denklemin çözümlerinin yapısıyla ilgili olarak bir çok bilgi ortaya çkarır.
Kartezyen Koordinat Sistemi
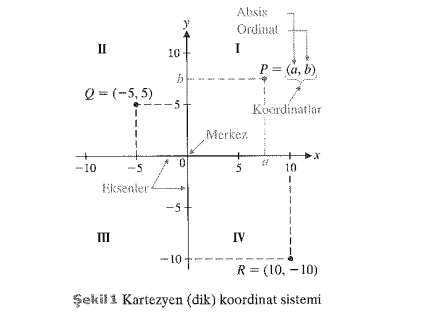
Düzlemde bir Kartezyen koordinat sistemi (veya dik koordinat sistemi) elde etmek için -biri yatay ve biri dikey- olmak üzere iki reel sayı doğrusu çizilerek bu doğruların ortak noktasına Şekil 1 de gösterildiği gibi orijin veya (başlangiç noktası) adı verildiğini hatırlayını. Dik koordinat sistemindeki iki doğrunun üst ve sağ tarafları pozitif yönler için doğal seçeneklerdir. Bu iki sayı doğrusu, yatay eksen ve dikey eksen ya da ikisi birlikte koordinat eksenleri olarak adlandırlır. Yatay eksen genel olarak $\boldsymbol{x}$ ekseni ve dikey eksen $\boldsymbol{y}$ ekseni olarak adlandırilır ve ilgili harflerle belirtilir. Koordinat eksenleri, düzlemi dördül (kadran) olarak adlandırlan ve saat yönünü̉ tersine I den IV e kadar suralanan dört bölgeye ayırır (bkn. Şek. 1).
Şimdi düzlemdeki her bir nokta için bu noktanın koordinatlart adı verilen iki sayı belirleyeceğiz. Düzlemde rastgele verilmiş olan $P$ noktası için, bu noktadan Şekil 1 deki gibi yatay ve dikey çizgiler çizelim. Dikey çizgi yatay ekseni bir a noktasinda, yatay çizgi dikey ekseni bir $b$ noktasında keser. Bu iki sayı, $(a, b)$ biçiminde smralı çift olarak yazılır ve $P$ noktasmın koordinatları gösterir. İlk koordinat olan $a, P$ nin absisi; ikinci koordinat olan $b$ ise $P$ nin ordinat olarak adlandrrlır. Şekil 1 de $Q$ nun yatay koordinatı -5 ve dikey koordinatı 5 tir. Herhangi bir noktanın koordinatları eksen isimleri ile de tanmlanabilir. Şekil 1 de $R$ noktasinın absisi 10 ve ordinatn -10 dur. $(0,0)$ koordinatları merkez (orijin) olarak adlandırlan O noktasınm koordinatlaridir.
Yukarıda açıklamış olduğumuz süreç, düzlemdeki her bir $P$ noktasına $(a, b)$ gibi reel sayılar çifti karşllk getirir. Karşit olarak $(a, b)$ gibi reel sayılardan oluşan bir sayı çifti verildiğinde bu ikiliye düzlemde bir $P$ noktası karşılk gelir. Bu durumu şöyle anlatabiliriz:
Bir diulemdefi nokbahar ile tim reel sayu ilkilleri arasnda birebir bix eshere vardir.
数学代写|微积分代写Calculus代考|Ax+B y=C Denkleminin Grafiği
Bölüm 1-1 de $a x+b=0(a \neq 0)$ biçimindeki denklemi, bir değişkenli dogrusal denklem olarak adlandırmıştık. Şimdi iki değişkenli doğrusal denklemleri inceleyeceğiz:
TANIM Iki Değişenli Doğrusal Denklemler
Iki değişkenli doğrusal denklem, $A, B$ ve $C$ nin sabit ( $A$ ve $B$ nin ikisinin de 0 olmadiğı), $x$ ve $y$ nin değisken olduğu,
$$
A x+B y=C
$$
biçiminde bir eşitliktir. Iki değişkenli doğrusal denklemin yukardaki biçimine, onun standart formu denir.
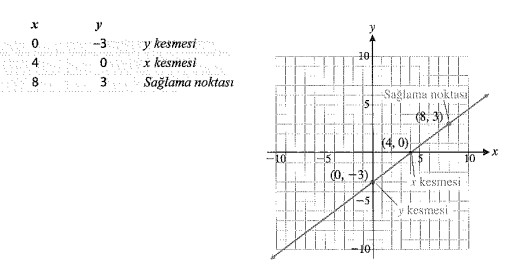
İki değişkenli denklemin bir çözümü, denklemi doğrulayan bir sıralı reel sayı ikilisidir. Örneğin, $3 x-2 y=6$ nın bir çözümü $(4,3)$ tür. İki değişkenli denklemin çözïm kümesi, denklemi sağlayan tüm ikililerin kümesidir. Bir denklemin grafiği, denklemin çözüm kümesine dik koordinat sisteminde karşılık gelen noktaların kümesidir.
(A) Yukarıda $3 x-2 y=6$ nın bir çözümü $(4,3)$ tür.
Bu denklem için üç tane daha çözüm bulunuz. Bu çözümleri dik koordinat sisteminde gösteriniz. Bu denklemin çözüm kümesini düzlemde göstermek için bilinen bir geometrik şekil kullanılabilir mi?
(B) $x=2$ denklemi için (A) da sorulanları tekrarlayınız.
(C) $y=-3$ denklemi için (A) da sorulanları tekrarlaymız.
Araştırma ve Tartışma 1 de, $A x+B y=C$ biçimindeki her denklemin grafiğinin bir doğru olacağı izlenimini edinmiş olmalısınız. Teorem 1, bu izlenimin doğru olduğunu anlatir.
微积分代写
数学代写|微积分代写Calculus代考|Graffkler ve Doğrular
在本章中,我们将分析最基本的几何图形之一,即线。当我们在本书中使用线这个术语时,我们将指几何意义上的直线。我们将学习如何识别直线,如何绘制它的图形,以及如何利用有关直线的信息来寻找它的方程。分析一个方程的图形可以发现很多关于方程解的结构的信息。
笛卡尔坐标系
回顾一下,为了获得平面内的直角坐标系(或称正交坐标系),需要绘制两条实数线–一条水平线和一条垂直线,它们的共同点被称为原点,如图1所示。在垂直坐标系中,两条线的上边和右边是正方向的自然选择。这两条数线,即横轴和纵轴,或两者都是,被称为坐标轴。水平轴一般被称为$boldsymbol{x}$轴,垂直轴被称为$boldsymbol{y}$轴,用相应的字母表示。坐标轴将平面划分为四个区域,称为象限,从I到IV逆时针行进(见图1)。
对于平面上的每一个点,我们现在将确定两个数字,称为这个点的坐标。对于平面内的一个任意点$P$,让我们从这个点开始画水平线和垂直线,如图1。垂直线在$a$处与横轴相交,水平线在$b$处与纵轴相交。这两个数字以$(a, b)$的形式写成有符号的一对,表示点$P$的坐标。第一个坐标$a$被称为$P$的横坐标,第二个坐标$b$被称为$P$的纵坐标。在图1中,Q$的横坐标是-5,纵坐标是5。任何点的坐标也可以用轴名来定义。在图1中,$R$的横轴是10,纵轴是-10。$(0,0)$的坐标是点O的坐标,它被称为中心(原点)。
我们上面描述的过程是通过一对实数$(a,b)$来对应平面内的每一个点$P$。反过来说,给定一对实数$(a, b)$,这对实数对应于平面内的一个点$P$。我们可以把这种情况解释如下:
平面内的一个点和一对实数基元之间存在着一对一的对应关系。
数学代写|微积分代写Calculus代考|Ax+B y=C Denkleminin Grafiği
在第1-1章中,我们称$a x+b=0(a\neq 0)$ 的方程为单变量的线性方程。 现在我们将研究双变量的线性方程:
定义 双变量线性方程
双变量线性方程,其中$A、B$和$C$是常数($A$和$B$不都是0),$x$和$y$是变量、
$$
A x+B y=C
$$
是一个平等的形式。上述形式的两个变量的线性方程被称为其标准形式。
一个双变量方程的解是一对满足该方程的有序实数。例如,3x-2 y=6$的解是$(4,3)$。一个双变量方程的解集是所有满足该方程的对的集合。方程的图形是坐标系中与方程的解集垂直的点的集合。
(A) 上面3 x-2 y=6$的一个解是$(4,3)$。
再找出这个方程的三个解。在正交坐标系中显示这些解。能否用一个已知的几何图形来表示这个方程在平面上的解集?
(B) 对方程$x=2$重复(A)中的问题。
(C) 对方程$y=3$重复(A)。
从调查和讨论1中,你应该有这样的印象:每一个形式为$A x+B y=C$的方程的图形都是一条直线。定理1表明,这一印象是正确的。

数学代写|微积分代写Calculus代考 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。
微观经济学代写
微观经济学是主流经济学的一个分支,研究个人和企业在做出有关稀缺资源分配的决策时的行为以及这些个人和企业之间的相互作用。my-assignmentexpert™ 为您的留学生涯保驾护航 在数学Mathematics作业代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的数学Mathematics代写服务。我们的专家在图论代写Graph Theory代写方面经验极为丰富,各种图论代写Graph Theory相关的作业也就用不着 说。
线性代数代写
线性代数是数学的一个分支,涉及线性方程,如:线性图,如:以及它们在向量空间和通过矩阵的表示。线性代数是几乎所有数学领域的核心。
博弈论代写
现代博弈论始于约翰-冯-诺伊曼(John von Neumann)提出的两人零和博弈中的混合策略均衡的观点及其证明。冯-诺依曼的原始证明使用了关于连续映射到紧凑凸集的布劳威尔定点定理,这成为博弈论和数学经济学的标准方法。在他的论文之后,1944年,他与奥斯卡-莫根斯特恩(Oskar Morgenstern)共同撰写了《游戏和经济行为理论》一书,该书考虑了几个参与者的合作游戏。这本书的第二版提供了预期效用的公理理论,使数理统计学家和经济学家能够处理不确定性下的决策。
微积分代写
微积分,最初被称为无穷小微积分或 “无穷小的微积分”,是对连续变化的数学研究,就像几何学是对形状的研究,而代数是对算术运算的概括研究一样。
它有两个主要分支,微分和积分;微分涉及瞬时变化率和曲线的斜率,而积分涉及数量的累积,以及曲线下或曲线之间的面积。这两个分支通过微积分的基本定理相互联系,它们利用了无限序列和无限级数收敛到一个明确定义的极限的基本概念 。
计量经济学代写
什么是计量经济学?
计量经济学是统计学和数学模型的定量应用,使用数据来发展理论或测试经济学中的现有假设,并根据历史数据预测未来趋势。它对现实世界的数据进行统计试验,然后将结果与被测试的理论进行比较和对比。
根据你是对测试现有理论感兴趣,还是对利用现有数据在这些观察的基础上提出新的假设感兴趣,计量经济学可以细分为两大类:理论和应用。那些经常从事这种实践的人通常被称为计量经济学家。
Matlab代写
MATLAB 是一种用于技术计算的高性能语言。它将计算、可视化和编程集成在一个易于使用的环境中,其中问题和解决方案以熟悉的数学符号表示。典型用途包括:数学和计算算法开发建模、仿真和原型制作数据分析、探索和可视化科学和工程图形应用程序开发,包括图形用户界面构建MATLAB 是一个交互式系统,其基本数据元素是一个不需要维度的数组。这使您可以解决许多技术计算问题,尤其是那些具有矩阵和向量公式的问题,而只需用 C 或 Fortran 等标量非交互式语言编写程序所需的时间的一小部分。MATLAB 名称代表矩阵实验室。MATLAB 最初的编写目的是提供对由 LINPACK 和 EISPACK 项目开发的矩阵软件的轻松访问,这两个项目共同代表了矩阵计算软件的最新技术。MATLAB 经过多年的发展,得到了许多用户的投入。在大学环境中,它是数学、工程和科学入门和高级课程的标准教学工具。在工业领域,MATLAB 是高效研究、开发和分析的首选工具。MATLAB 具有一系列称为工具箱的特定于应用程序的解决方案。对于大多数 MATLAB 用户来说非常重要,工具箱允许您学习和应用专业技术。工具箱是 MATLAB 函数(M 文件)的综合集合,可扩展 MATLAB 环境以解决特定类别的问题。可用工具箱的领域包括信号处理、控制系统、神经网络、模糊逻辑、小波、仿真等。