MY-ASSIGNMENTEXPERT™可以为您提供mathstat MATH2300 Mathematical Modeling数学建模的代写代考和辅导服务!
这是戴尔豪斯大学数学建模课程的代写成功案例。
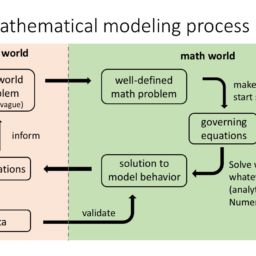
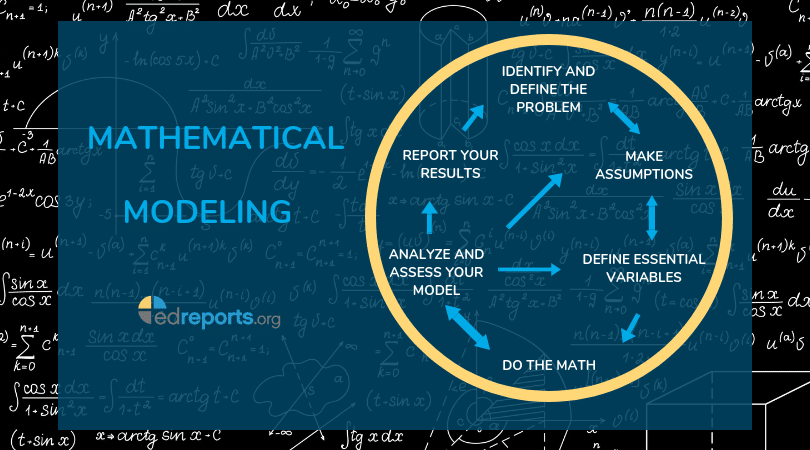
MATH2300课程简介
(3) Credit Hours
Lab-based activities designed to strengthen and expand knowledge of topics in secondary mathematics, focusing on topics from precalculus and elementary calculus. Explorations will involve the use of multiple representations, transformations, data analysis techniques and interconnections among geometry, probability and algebra. Most labs will include significant use of various technologies. The use of quantitative approaches and building relationships between discrete and continuous reasoning will be recurrent themes. Every semester. Prerequisites: Admissions to the UTeaChattanooga program; university, UTSM, and major department grade point averages of at least 2.5; UTSM 1020 and MATH 1920, MATH 1921 and MATH 2200 with minimum grades of C or UTeaChattanooga Co-Director approval.
Prerequisites
Course outline: Dynamical systems, basic probability, queing theory, selected topics.
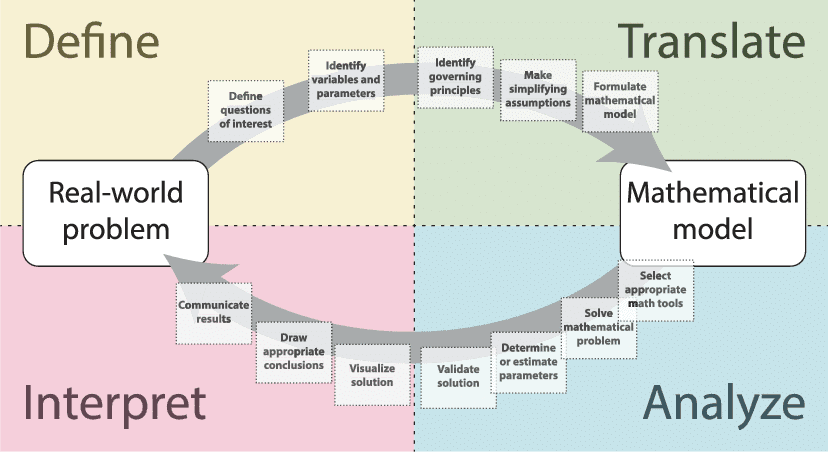
References: The textbook for this course is “A Course in Mathematical Modeling” by Mooney and Swift. Some of the material will be outside the textbook in which case appropriate references will be provided.
Advising and Access Services Center: Students may request accommodation as a result of barriers related to disability, religious obligation, or any characteristic under the Nova Scotia Human Rights Act. Students who require academic accommodation for either classroom participation or the writing of tests and exams should make their request to the Advising and Access Services Center (AASC) prior to or at the outset of the regular academic year. Please visit www.dal.ca/access for more information and to obtain the Request for Accommodation – Form A.
MATH2300 Mathematical Modeling HELP(EXAM HELP, ONLINE TUTOR)
a. Show that the general solution of the $\mathrm{DE} x^2 \frac{d y}{d x}=y^2$ is $y(x)=\frac{x}{C x+1}$.
b. For $\mathrm{EACH}$ of the ICs (i) $y(4)=-4$ and (ii) $y(1)=2$ :
substitute the given IC to find the unique solution of the IVP;
state the domain of validity (remember that it must include the initial point); and
sketch the solution, labelling any vertical and/or horizontal asymptotes.
c. The general solution reveals that there are many solutions through $(0,0)$. Show that every solution through $(0,0)$ has slope $y^{\prime}(0)=1$, and this common tangent line is itself a solution of the DE. Add this tangent line, and some other typical solutions through $(0,0)$, to your sketch in b.
d. Does the existence of multiple differentiable solutions through $(0,0)$ violate the Existence-Uniqueness Theorem? Explain why, or why not.
Suppose a pot of soup has been simmering on the stove at $100^{\circ} \mathrm{C}$. For storage in the fridge, it should not be warmer than $20^{\circ} \mathrm{C}$. Initially, we cool it in a sink full of $5^{\circ} \mathrm{C}$ water (running the water to keep it cold).
a. Let $t=0$ when the soup pot was removed from the stove. If the soup cools to $60^{\circ} \mathrm{C}$ after 10 minutes, what is the value of the rate constant $k$ ? (You may use the known solution from Module 1.)
b. With the soup at $60^{\circ} \mathrm{C}$, we remove the pot from the sink and set it on the counter to finish cooling. If the room temperature is $15^{\circ} \mathrm{C}$, how much longer will it be until we can put it in the fridge?
If the energy required to both maintain existing cells and create new cells is taken into account, then it can be shown that the mass $m$ of a living organism grows according to the IVP
$$
\frac{d m}{d t}=a m^{\frac{3}{4}}\left(1-\left(\frac{m}{M}\right)^{\frac{1}{4}}\right), m(0)=m_0,
$$
where $a$ and $M$ are positive constants with $[M]=\mathcal{M}$, and $[a]^4=\mathcal{M} \mathcal{T}^{-4}$.
a. Give a physical interpretation of the constant $M$. [HINT: What has happened to the organism if $\frac{d m}{d t}=0$ ?]
b. Show that, in terms of a new variable $y=1-\left(\frac{m}{M}\right)^{\frac{1}{4}}$, the IVP becomes
$$
\frac{d y}{d t}=-k y, \quad y(0)=y_0
$$
where $k=\frac{a}{4 M^{\frac{1}{4}}}$, and $y_0=1-\left(\frac{m_0}{M}\right)^{\frac{1}{4}}$.
c. Write down the well-known solution of the IVP in part b., and hence find the solution of the IVP in a..
d. Given numeric values $M=16, m_0=1$, and $a=2$ for the constants, use Maple to plot the solution $m(t)$ for $0 \leq t \leq 25$, and estimate the time $t^$ at which the organism reaches half its ultimate size. e. Explain how you could use the result of part c. to get a more accurate estimate of $t^$.
i. Read carefully the preamble to problem 12 of section 2.2 of your text (section 2.3 of Edition 1) on the use of carbon-14 $\left({ }^{14} \mathrm{C}\right)$ for dating archeological artifacts. Then answer each of parts a), b), and c) in that question.
ii. Show that the variables $y=\frac{Q}{Q_0}$ and $\tau=r t$ are dimensionless, and that the equivalent dimensionless IVP is $\frac{d y}{d \tau}=-y, y(0)=1$
iii. Search the web for “The Great hall and Round Table in Winchester” and read about this amazing oak table and its link to the legend of King Arthur and his Knights. In 1976 , one of several tests on the table revealed that it contained $91.02 \%$ of the amount of ${ }^{14} \mathrm{C}$ in living wood. Use the solution of the IVP in part ii to determine the value of $\tau$ when $y=0.9102$. Then convert your answer back to years. Given that King Arthur lived in the $5^{\text {th }}$ century AD, could the table have been his famous Round Table?

MY-ASSIGNMENTEXPERT™可以为您提供MATHSTAT MATH2300 MATHEMATICAL MODELING数学建模的代写代考和辅导服务!