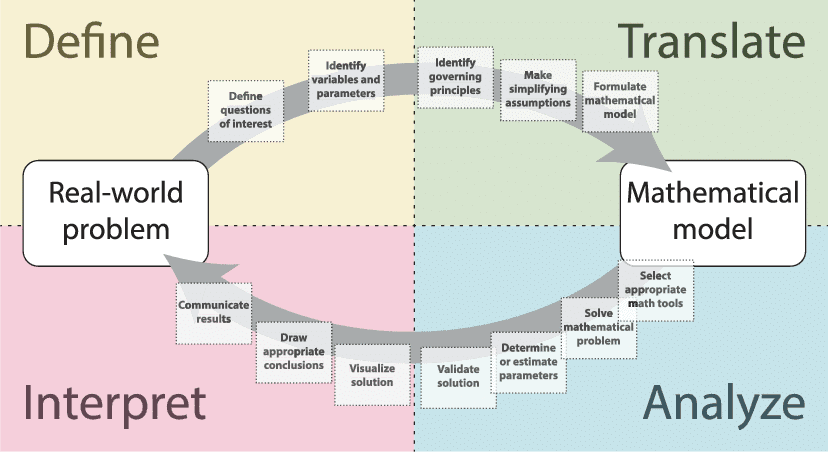
MY-ASSIGNMENTEXPERT™可以为您提供sydney MATH1013 Mathematical Modeling数学建模的代写代考和辅导服务!
这是悉尼大学数学建模课程的代写成功案例。

MATH1013课程简介
MATH1013 is designed for science students who do not intend to undertake higher year mathematics and statistics. In this unit of study students learn how to construct, interpret and solve simple differential equations and recurrence relations. Specific techniques include separation of variables, partial fractions and first and second order linear equations with constant coefficients. Students are also shown how to iteratively improve approximate numerical solutions to equations.
Prerequisites
At the completion of this unit, you should be able to:
- LO1. write down general and particular solutions to simple differential equations and recurrence relations describing models of growth and decay
- LO2. determine the order of a differential equation or recurrence relation
- LO3. find equilibrium solutions and analyse their stability using both graphical methods and slope conditions
- LO4. recognise and solve separable first-order differential equations
- LO5. use partial fractions and separation of variables to solve certain nonlinear differential equations, including the logistic equation
- LO6. use a variety of graphical and numerical techniques to locate and count solutions to equations
- LO7. solve equations numerically by fixed-point iteration, including checking if an iteration method is stable
- LO8. explore sequences numerically, and classify their long-term behaviour
- LO9. determine the general solution to linear second-order equations or simultaneous pairs of first order equations with constant coefficients.
MATH1013 Mathematical Modeling HELP(EXAM HELP, ONLINE TUTOR)
A coal miner is trapped in a cave-in after an explosion. He lies in a small chamber (volume $50 \mathrm{~m}^3$ ) into which air containing $100 \mathrm{~g} / \mathrm{m}^3$ of carbon monoxide (CO) is seeping at a rate of $0.001 \mathrm{~m}^3$ per minute, and from which the well-mixed $\mathrm{CO}$ and air is leaking at the same rate.
a. State an IVP for the quantity $Q(t) \mathrm{g}$ of $\mathrm{CO}$ in the cave for $t \geq 0$, assuming the chamber was free of $\mathrm{CO}$ at the time of the cave-in.
b. Solve the IVP in a.
c. Given that $\mathrm{CO}$ at a concentration of $1200 \mathrm{ppm}$ ( or $\approx 1.4 \mathrm{~g} / \mathrm{m}^3$ ) is lethal to human beings, how long do his rescuers have to reach him?
In Module 1, Section 1, Lecture B iii a, the video shows the development of Toricelli’s Law. One of the assumptions made is that the stream of water exiting a asmall hole of cross-sectional area $a$ in the bottom of a tank retains that cross-section. If you’ve ever watched the flow of water from a tap, you’ll know that’s not the case – the column of water actually narrows as it exits the tap. This motivates the introduction of a dimensionless contraction coefficient $\alpha$, so that the volume of water leaving the tank per unit time through the hole is assumed to be $\alpha a \sqrt{2 g h}$, rather than just $a \sqrt{2 g h}$, where $h$ is the depth of water in the tank.
a. Suppose a cylindrical tank with constant cross-sectional area $A$ has a small hole of area $a$ at the bottom. If water is pumped into the tank at a constant rate $r \mathrm{~m}^3$ per minute, justify this DE for the depth $h(t)$ of water in the tank:
$$
\frac{d h}{d t}=\frac{r-\alpha a \sqrt{2 g h}}{A} .
$$
b. Find the equilibrium solution $h_e$ of this $\mathrm{DE}$, and give a physical interpretation.
c. If the tank has height $H$, state a condition for the equilibrium solution to be physically meaningful. (Ask yourself what happens if $r$ is too large.)
d. At $t=0$, the pump is turned off (i.e., $r=0$ ) just as $h=3 \mathrm{~m}$. If $A=\pi \mathrm{m}^2$, $a=0.01 \pi \mathrm{m}^2, \alpha=0.6$ for water, and $g=9.8 \mathrm{~ms}^{-2}$, how long will it take the tank to empty?
At $t=0$, a well-circulated pond with $10^6$ litres of water contains a bacterial pollutant at a concentration of $0.01 \mathrm{~kg}$ per litre. Bacteria-free water drains into the pond at a rate of 2400 litres per day, and pure water evaporates from the pond surface (leaving the bacteria behind) at a rate of 1200 litres per day.
a. Find the volume $V(t)$ of fluid in the pond for $t \geq 0$.
b. Find the quantity $Q_0$ of bacterial pollutant in the pond at time $t=0$, and explain why it does not change.
c. Show that the concentration $C(t)=\frac{Q_0}{V(t)}$ of bacterial pollutant decreases very slowly by determining how long it takes to drop to $0.001 \mathrm{~kg}$ per litre.
d. You realize that you forgot to allow for the fact that the bacteria in the pond also reproduce at a rate $r Q(t)$ kg per day. Find the quantity $Q(t)$ of bacteria for $t \geq 0$, using $Q(0)=Q_0$. Then show that if $r \geq 0.0012$ per day, the concentration $C(t)=\frac{Q(t)}{V(t)}$ never decreases (i.e., $\frac{d C}{d t} \geq 0$ for all $t \geq 0$ ).
The intricately rough surface of a grain of pollen, its size, and other features, result in motion subject to viscous damping.
Thus, assuming displacement positive upward, a grain of pollen of mass $m$ falls from rest according to the IVP
$$
m \frac{d v}{d t}=-m g-\gamma v, \quad v(0)=0
$$
with known solution
$$
v(t)=-\frac{m g}{\gamma}\left(1-e^{-\frac{1}{m} t}\right)
$$
If we observe that a grain of pollen of known mass falls to earth from a height of $1 \mathrm{~m}$ after $25 \mathrm{~s}$, can we find the drag coefficient $\gamma$ from this data? Let’s see.
a. Find the displacement $s(t)$ by solving the IVP
$$
\frac{d s}{d t}=-\frac{m g}{\gamma}\left(1-e^{-\frac{\chi}{m} t}\right), s(0)=1
$$
b. Show that, in terms of the ratio $x=\frac{\gamma}{m}$, setting $s(t)=0$ gives the equation
$$
0=-\frac{g}{x^2}\left(e^{-x t}+x t-\frac{x^2}{g}-1\right)
$$
In particular, with $t=25 \mathrm{~s}$ and $g=9.8 \mathrm{~ms}^{-2}$, we see that $s(25)=0$ is equivalent to
$$
\frac{1}{9.8} x^2-25 x+1=e^{-25 x}
$$
c. Obviously one solution of this equation is $x=0$ (not too useful). Use Maple plots to narrow down the possible solution to around $x=245$. Since this clearly occurs at the greater positive root of the quadratic, find its roots, verifying that $x=244.96 \mathrm{~s}^{-1}$ to two decimals.
d. Now comes the fun part. We will use data for the pollen of Amaranthus palmeri, assuming a spherical grain with diameter $30 \mu \mathrm{m}$ and density $1435 \mathrm{~kg} \mathrm{~m}^{-3}$. Find the mass $m$, and use the solution from part c. to find the drag coefficient $\gamma$.
e. The researchers found that for a grain of pollen with the properties of part d., the terminal velocity had magnitude of about $4 \mathrm{~cm} \mathrm{~s}^{-1}$. Do your results from c. and d. confirm that value?

MY-ASSIGNMENTEXPERT™可以为您提供SYDNEY MATH1013 MATHEMATICAL MODELING数学建模的代写代考和辅导服务!