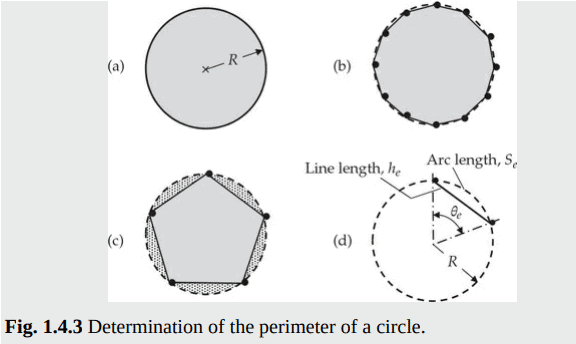
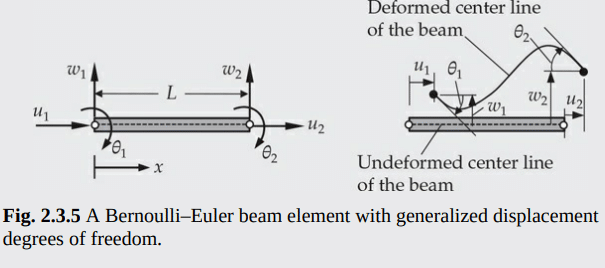
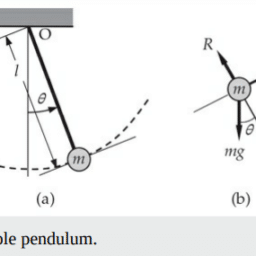
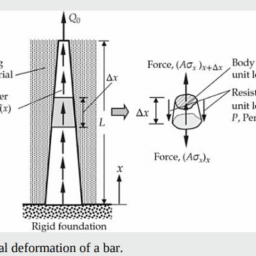
MY-ASSIGNMENTEXPERT™可以为您提供engineering MATH4604 Finite Element MethoD有限元方法的代写代考和辅导服务!
这是普渡大學有限元方法的代写成功案例。
CE595课程简介
• Academic integrity is expected of all students at all times. Further information on academic integrity policies may be found in the handbook University Regulations and on the Web at http://www.purdue.edu/ODOS/osrr/integrity.htm.
• Homework is due in class on the date indicated. In general, no late homework will be accepted. If you feel that you have serious extenuating circumstances (eg., illnesses or accidents requiring medical attention, personal or family crises), you must discuss your situation with Dr. Varma as soon as possible. In particular, foreseeable conflicts with due dates (eg., interviews, participation in sports activities, religious observances, etc.) must be brought to our attention before the due date.
• It is anticipated, even encouraged, that students will consult with each other on homework assignments. It is expected, however, that all work submitted by the student represent his/her own effort. Instances of plagiarism on an assignment will result in full loss of credit for that assignment.
• Instances of cheating in any form during an exam will result in full loss of credit for that exam. Additional measures, including immediate failure of the course, may be applied at the discretion of the instructor and/or University staff.
• Students who have documented disabilities and require accommodations must make an appointment with Dr. Varma to discuss their needs by the end of the second week of class. Students with disabilities must be registered with Adaptive Programs in the Office of the Dean of Students before classroom accommodations can be provided.
Prerequisites
Grades will be based upon the following elements:
• Homework (25% of total grade) Due in class at dates to be announced.
• Hourly Exam #1 (25% of total grade) Tentatively scheduled for February last week.
• Hourly Exam #2 (25% of total grade) Tentatively scheduled for April first week.
• Course Project or Final Exam (25% of total grade) Schedule will be announced later in the semester.
CE595 Finite Element Method HELP(EXAM HELP, ONLINE TUTOR)
Given a rectangular element $\square_k$, with horizontal and vertical edges of lengths $h x, h y$, respectively, let $\pi_h^1$ be the standard bilinear interpolant, which agrees with the underlying function at the four vertices. Show that
$$
\begin{aligned}
\left|\nabla\left(u-\pi_h^1 u\right)\right|_{\mathbf{\square}k}^2 & \leq \max \left{\frac{h x}{h y}, \frac{h y}{h x}\right}\left|\nabla\left(\bar{u}-\pi_h^1 \bar{u}\right)\right|{\mathbf{a}}^2, \ \left|D^2 \bar{u}\right|{\mathbf{a}}^2 & \leq \frac{h_k^2}{4} \max \left{\frac{h x}{h y}, \frac{h y}{h x}\right}\left|D^2 u\right|{\mathbf{q}_k}^2,
\end{aligned}
$$
where $h_k=\max {h x, h y}$.
Let $V_h$ be a $P_1$ finite element space on a triangulation $T_h$ of a domain $\Omega \subset \mathbb{R}^2$. Given $u \in H^2(\Omega)$ let $u_h \in V_h$ be the solution of the boundary value problem:
$$
\int_{\Omega} u_h v=\int_{\Omega} u v \quad \text { for all } v \in V_h .
$$
Thus, $u_h$ is the $L_2$-projection of $u$ onto $V_h$.
Prove the error estimate
$$
\left|u-u_h\right| \leq \inf _{v_h \in V_h}\left|u-v_h\right|
$$
and show that $\left|u_h\right| \leq|u|$.
By establishing a standard $L_2$ interpolation estimate, establish the bound
$$
\left|u-u_h\right| \leq C h^2|u|_2
$$
Build a finite element (FE) model and find elongation of a bar rotating about one of the ends with the circular frequency $\omega$. Use 1 and 2 finite elements.
$l$ – length, $E$ – Young modulus, $A$ – cross-sectional area, $\rho$-density. Compare the results with the exact analytical solution.
Write the system of FEM equations for a 2-D truss (after including the displacement boundary conditions) and find the displacement vector of the joint loaded be force $P$. $E$ – Young modulus, $A$ – cross-sectional area. $\alpha=45^{\circ}$.
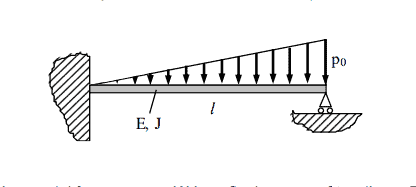
Find the beam deflection and the bending moment and shear force distributions. Compare results obtained for the Ritz method (with approximate functions of 1 and 2 parameters) and for FEM ( 1 and 2 finite beam elements)

MY-ASSIGNMENTEXPERT™可以为您提供ENGINEERING MATH4604 FINITE ELEMENT METHOD有限元方法的代写代考和辅导服务!