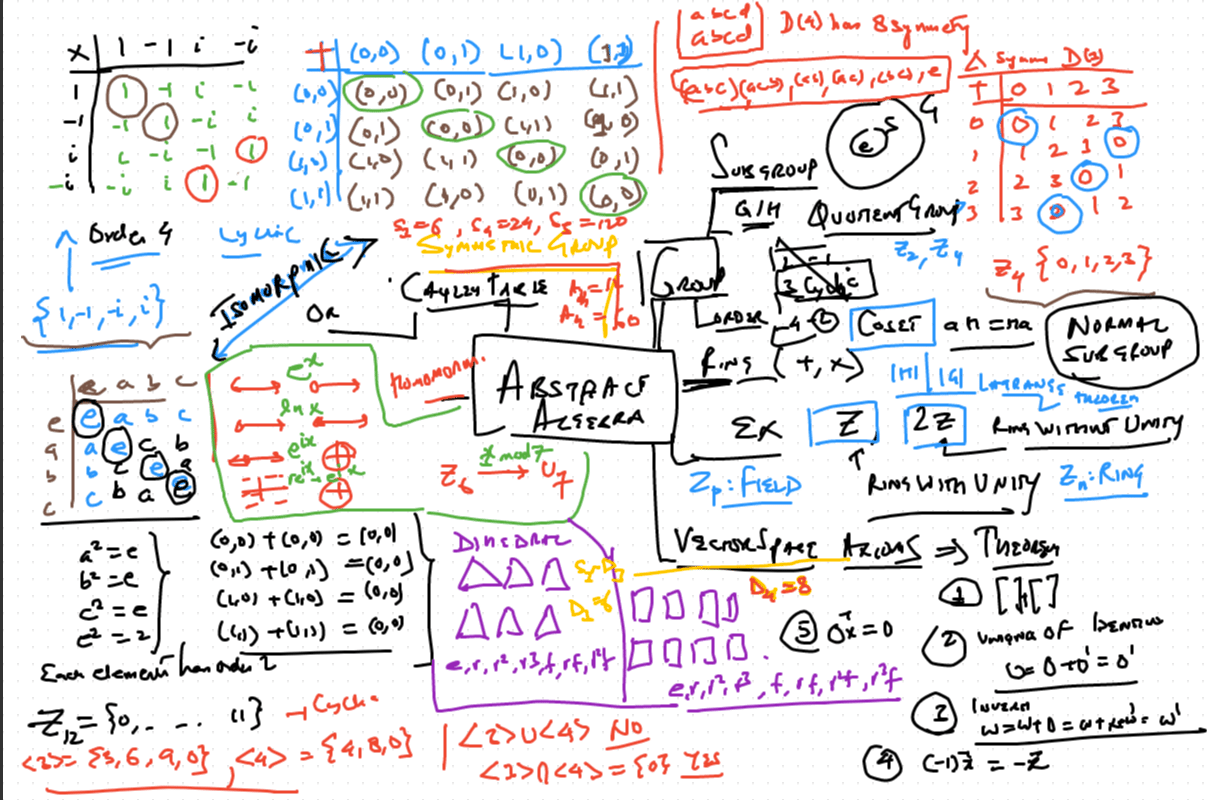
如果你也在 怎样代写现代代数Modern Algebra 这个学科遇到相关的难题，请随时右上角联系我们的24/7代写客服。现代代数Modern Algebra现代代数，也叫抽象代数，是数学的一个分支，涉及各种集合（如实数、复数、矩阵和矢量空间）的一般代数结构，而不是操作其个别元素的规则和程序。除了数论和代数几何的发展，现代代数通过群论对对称性有重要的应用。群这个词通常指的是一组运算，可能保留了某些物体的对称性或类似物体的排列。

现代代数Modern Algebra代数是数学的一个分支的名称，但它也是一种数学结构的名称。代数或代数结构是一个带有运算的非空集合。从一般结构角度研究代数的数学分支被称为普遍代数。相比之下，现代代数处理的是特殊类别的代数，包括群、环、场、向量空间和模块。从普遍代数的角度来看，场、向量空间和模块不被视为代数结构。现代代数也被称为抽象代数，但这两个名字在今天都有误导性，因为它在现代数学中已经不怎么现代或抽象了。

现代代数Modern Algebra代写，免费提交作业要求， 满意后付款，成绩80\%以下全额退款，安全省心无顾虑。专业硕 博写手团队，所有订单可靠准时，保证 100% 原创。最高质量的现代代数Modern Algebra作业代写，服务覆盖北美、欧洲、澳洲等 国家。 在代写价格方面，考虑到同学们的经济条件，在保障代写质量的前提下，我们为客户提供最合理的价格。 由于作业种类很多，同时其中的大部分作业在字数上都没有具体要求，因此现代代数Modern Algebra作业代写的价格不固定。通常在专家查看完作业要求之后会给出报价。作业难度和截止日期对价格也有很大的影响。

同学们在留学期间，都对各式各样的作业考试很是头疼，如果你无从下手，不如考虑my-assignmentexpert™！

my-assignmentexpert™提供最专业的一站式服务：Essay代写，Dissertation代写，Assignment代写，Paper代写，Proposal代写，Proposal代写，Literature Review代写，Online Course，Exam代考等等。my-assignmentexpert™专注为留学生提供Essay代写服务，拥有各个专业的博硕教师团队帮您代写，免费修改及辅导，保证成果完成的效率和质量。同时有多家检测平台帐号，包括Turnitin高级账户，检测论文不会留痕，写好后检测修改，放心可靠，经得起任何考验！

想知道您作业确定的价格吗? 免费下单以相关学科的专家能了解具体的要求之后在1-3个小时就提出价格。专家的 报价比上列的价格能便宜好几倍。

我们在数学Mathematics代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的数学Mathematics代写服务。我们的专家在现代代数Modern Algebra代写方面经验极为丰富，各种现代代数Modern Algebra相关的作业也就用不着说。

数学代写|现代代数代考Modern Algebra代写|Distributed data structures

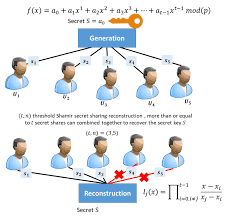
We start with another problem from cryptography: secret sharing. Suppose that, for some positive integer $n$, we have $n$ players that want to share a common secret in such a way that all of them together can reconstruct the secret but any subset of $n-1$ of them or less cannot do so. The reader may imagine that the secret is a key in a cryptosystem or a code guarding a common bank account or inheritance, or an authorization for a financial transaction of a company which requires the signature of a certain number of managers. This can be solved by using interpolation (Section 5.2), as follows.
We choose $2 n-1$ values $f_1, \ldots, f_{n-1}, u_0, \ldots, u_{n-1}$ in a field $F$ (say, $F$ is $\mathbb{Q}$ or a finite field) such that the $u_i$ are distinct, and let $f$ be the polynomial $f_{n-1} x^{n-1}+$ $\cdots+f_1 x+f_0$, where $f_0 \in F$ is the secret, encoded in an appropriate way. Then we give $v_i=f\left(u_i\right)=f_{n-1} u_i^{n-1}+\cdots+f_1 u_i+f_0$ to player $i$. The reconstruction of the polynomial $f$ from its values $v_0, \ldots, v_{n-1}$ at the $n$ distinct points $u_0, \ldots, u_{n-1}$ is called interpolation and may be performed, for example, by using the Lagrange interpolation formula (Section 5.2). The interpolating polynomial at $n$ points of degree less than $n$ is unique, and hence all $n$ players together can recover $f$ and the secret $f_0$, but one can show that any proper subset of them can obtain no information on the secret. More precisely, all elements of $F$-as potential values of $f_0$-are equally consistent with the knowledge of fewer than $n$ players. We discuss the secret sharing scheme in Section 5.3.
Essentially the same scheme works for a different problem: reliable routing. Suppose that we want to send a message consisting of several packets over a network (for example, the internet) that occasionally loses packets. We want to encode a message of length $n$ into not many more than $n$ packets in such a way that after a loss of up to $l$ arbitrary packets the message can still be recovered. Such a scheme is called an erasure code. (We briefly discuss the related error correcting codes, which are designed for networks that sometimes perturb packets but do not lose them, in Chapter 7.) An obvious solution would be to send the message $l+1$ times, but this increases message length and hence slows down communication speed by a factor of $l+1$ and is unacceptable even for small values of $l$.

数学代写|现代代数代考Modern Algebra代写|Computer algebra systems

We give a short overview of the computer algebra systems available at the time of writing. We do not present much detail, nor do we aim for completeness.
The vast majority of this book’s material is of a fundamental nature and technology-independent. But this short section and some other places where we discuss implementations date the book; if the rapid progress in this area continues as expected, some of this material will become obsolete in a short time.
Computer algebra systems have historically evolved in several stages. An early forerunner was Williams’ (1961) PMS, which could calculate floating point polynomial gcd’s. The first generation, beginning in the late $1960 \mathrm{~s}$, comprised MACSYMA from Joel Moses’s MATHLAB group at MIT, SCRATCHPAD from Richard Jenks at IBM, ReDUCE by Tony Hearn, and SAC-I (now SACLIB) by George Collins. MuMATH by David Stoutemyer ran on a small microprocessor; its successor DERIVE is available on the hand-held TI-92. These researchers and their teams developed systems with algebraic engines capable of doing amazing exact (or formal or symbolic) computations: differentiation, integration, factorization, etc. The second generation started with MAPLE by Keith Geddes and Gaston Gonnet from the University of Waterloo in 1985 and MATHEMATICA by Stephen Wolfram. They began to provide modern interfaces and graphic capabilities, and the hype surrounding the launching of MATHEMATICA did much to make these systems widely known. The third generation is on the market now: AXIOM, a successor of SCRATCHPAD, by NAG, MAGMA by John Cannon at the University of Sydney, and MUPAD by Benno Fuchssteiner at the University of Paderborn. These systems incorporate a categorical approach and operator calculations.
Today’s research and development of computer algebra systems is driven by three goals, which sometimes conflict: wide functionality (the capability of solving a large range of different problems), ease of use (user interface, graphics display), and speed (how big a problem you can solve with a routine calculation, say in a day on a workstation). This text will concentrate on the latter goal. We will see the basics of the fastest algorithms available today, mainly for some problems in polynomial manipulation. Several groups have developed software for these basic operations: PARI by Henri Cohen in Bordeaux, LIDIA by Johannes Buchmann in Darmstadt, NTL by Victor Shoup, and packages by Erich Kaltofen. William Stein’s open-source SAGE facilitates interoperability of various systems, and SINGULAR is strong in certain algebraic settings.

现代代数代写

数学代写|现代代数代考Modern Algebra代写|Distributed data structures

我们从密码学的另一个问题开始:秘密共享。假设，对于某个正整数n，我们有n个玩家想要共享一个共同的秘密，这样他们所有人都可以重建这个秘密，但是他们中的n-1个或更少的人不能这样做。读者可以想象，这个秘密是密码系统中的一个密钥，或者是保护普通银行账户或继承的代码，或者是需要一定数量的管理人员签名的公司金融交易的授权。这可以通过使用插值(第5.2节)来解决，如下所示。
我们在一个域$F$(假设$F$是$\mathbb{Q}$或一个有限域)中选择$2个n-1$值$f_1， \ldots, f_{n-1} $， u_0， \ldots, u_{n-1}$，使得$u_i$是不同的，并设$F$为多项式$f_{n-1} x^{n-1}+$ $\cdots+f_1 x+f_0$，其中F$中的$f_0 \是秘密，以适当的方式编码。然后我们给$ v_i = f \左(u_i \右)= f {n} u_i ^ {n} + \ cdots + f₁u_i + f_0球员我美元美元。从多项式$f$的值$v_0， \ldots, v_{n-1}$在$n$不同点$u_0， \ldots, u_{n-1}$处重建$f$称为插值，例如，可以使用拉格朗日插值公式(第5.2节)来执行。在小于n次的n个点上的插值多项式是唯一的，因此所有的n个参与者一起可以恢复f和秘密f_0，但是可以证明它们的任何适当子集都不能获得关于秘密的信息。更准确地说，$F$的所有元素-作为$f_0$的潜在值-同样与少于$n$玩家的知识一致。我们将在5.3节中讨论秘密共享方案。从本质上讲，相同的方案适用于不同的问题:可靠路由。假设我们希望通过偶尔丢失数据包的网络(例如internet)发送由几个数据包组成的消息。我们希望将长度为$n$的消息编码为不超过$n$的数据包，这样在丢失最多$l$任意数据包后，消息仍然可以恢复。这种方案称为擦除码。(我们在第7章中简要讨论了相关的纠错码，它是为有时干扰数据包但不丢失数据包的网络设计的。)一个明显的解决方案是发送消息$ 1 +1$次，但这会增加消息长度，从而以$ 1 +1$的系数降低通信速度，即使对于$l$的小值也是不可接受的。

数学代写|现代代数代考Modern Algebra代写|Computer algebra systems

我们给出了在写作时可用的计算机代数系统的简短概述。我们不提供太多细节，也不力求完整。
这本书的绝大部分材料都是基础性质的，与技术无关。但是这个简短的部分和其他一些我们讨论实现的地方是在书中;如果这一领域的快速进展如预期的那样继续下去，其中一些材料将在短时间内过时。
计算机代数系统在历史上经历了几个阶段的发展。早期的先驱是Williams(1961)的PMS，它可以计算浮点多项式的gcd。第一代，从1960年代末开始，包括麻省理工学院Joel Moses的MATHLAB小组的MACSYMA, IBM的Richard Jenks的SCRATCHPAD, Tony Hearn的ReDUCE和George Collins的SAC-I(现在的SACLIB)。David Stoutemyer设计的MuMATH运行在一个小型微处理器上;其继任者派生是可在手持TI-92。这些研究人员和他们的团队开发了具有代数引擎的系统，能够进行惊人的精确(或形式或符号)计算:微分，积分，分解等。第二代开始于1985年滑铁卢大学Keith Geddes和Gaston Gonnet的MAPLE和Stephen Wolfram的MATHEMATICA。它们开始提供现代的界面和图形功能，围绕MATHEMATICA发布的大肆宣传使这些系统广为人知。第三代已经上市了:NAG的SCRATCHPAD的继任者AXIOM，悉尼大学的John Cannon的MAGMA，以及帕德博恩大学的Benno Fuchssteiner的MUPAD。这些系统结合了分类方法和算子计算。
当今计算机代数系统的研究和发展是由三个目标驱动的，这三个目标有时会相互冲突:广泛的功能(解决大量不同问题的能力)，易用性(用户界面，图形显示)和速度(通过常规计算可以解决多大的问题，例如在工作站一天内)。本文将集中讨论后一个目标。我们将看到目前可用的最快算法的基础，主要用于多项式操作中的一些问题。几个小组已经为这些基本操作开发了软件:波尔多的Henri Cohen开发的PARI，达姆施塔特的Johannes Buchmann开发的LIDIA, Victor Shoup开发的NTL，以及Erich Kaltofen开发的软件包。William Stein的开源SAGE促进了各种系统的互操作性，并且SINGULAR在某些代数设置中很强大。

数学代写|现代代数代考Modern Algebra代写 请认准exambang™. exambang™为您的留学生涯保驾护航。

微观经济学代写

微观经济学是主流经济学的一个分支，研究个人和企业在做出有关稀缺资源分配的决策时的行为以及这些个人和企业之间的相互作用。my-assignmentexpert™ 为您的留学生涯保驾护航 在数学Mathematics作业代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的数学Mathematics代写服务。我们的专家在图论代写Graph Theory代写方面经验极为丰富，各种图论代写Graph Theory相关的作业也就用不着 说。

线性代数代写

线性代数是数学的一个分支，涉及线性方程，如：线性图，如：以及它们在向量空间和通过矩阵的表示。线性代数是几乎所有数学领域的核心。

博弈论代写

现代博弈论始于约翰-冯-诺伊曼（John von Neumann）提出的两人零和博弈中的混合策略均衡的观点及其证明。冯-诺依曼的原始证明使用了关于连续映射到紧凑凸集的布劳威尔定点定理，这成为博弈论和数学经济学的标准方法。在他的论文之后，1944年，他与奥斯卡-莫根斯特恩（Oskar Morgenstern）共同撰写了《游戏和经济行为理论》一书，该书考虑了几个参与者的合作游戏。这本书的第二版提供了预期效用的公理理论，使数理统计学家和经济学家能够处理不确定性下的决策。

微积分代写

微积分，最初被称为无穷小微积分或 “无穷小的微积分”，是对连续变化的数学研究，就像几何学是对形状的研究，而代数是对算术运算的概括研究一样。

它有两个主要分支，微分和积分；微分涉及瞬时变化率和曲线的斜率，而积分涉及数量的累积，以及曲线下或曲线之间的面积。这两个分支通过微积分的基本定理相互联系，它们利用了无限序列和无限级数收敛到一个明确定义的极限的基本概念 。

计量经济学代写

什么是计量经济学？
计量经济学是统计学和数学模型的定量应用，使用数据来发展理论或测试经济学中的现有假设，并根据历史数据预测未来趋势。它对现实世界的数据进行统计试验，然后将结果与被测试的理论进行比较和对比。

根据你是对测试现有理论感兴趣，还是对利用现有数据在这些观察的基础上提出新的假设感兴趣，计量经济学可以细分为两大类：理论和应用。那些经常从事这种实践的人通常被称为计量经济学家。

Matlab代写

MATLAB 是一种用于技术计算的高性能语言。它将计算、可视化和编程集成在一个易于使用的环境中，其中问题和解决方案以熟悉的数学符号表示。典型用途包括：数学和计算算法开发建模、仿真和原型制作数据分析、探索和可视化科学和工程图形应用程序开发，包括图形用户界面构建MATLAB 是一个交互式系统，其基本数据元素是一个不需要维度的数组。这使您可以解决许多技术计算问题，尤其是那些具有矩阵和向量公式的问题，而只需用 C 或 Fortran 等标量非交互式语言编写程序所需的时间的一小部分。MATLAB 名称代表矩阵实验室。MATLAB 最初的编写目的是提供对由 LINPACK 和 EISPACK 项目开发的矩阵软件的轻松访问，这两个项目共同代表了矩阵计算软件的最新技术。MATLAB 经过多年的发展，得到了许多用户的投入。在大学环境中，它是数学、工程和科学入门和高级课程的标准教学工具。在工业领域，MATLAB 是高效研究、开发和分析的首选工具。MATLAB 具有一系列称为工具箱的特定于应用程序的解决方案。对于大多数 MATLAB 用户来说非常重要，工具箱允许您学习和应用专业技术。工具箱是 MATLAB 函数（M 文件）的综合集合，可扩展 MATLAB 环境以解决特定类别的问题。可用工具箱的领域包括信号处理、控制系统、神经网络、模糊逻辑、小波、仿真等。