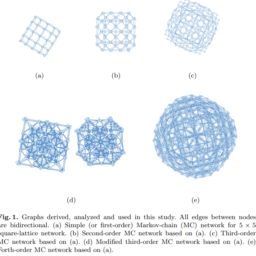
如果你也在 怎样代写复杂网络Complex Network 这个学科遇到相关的难题,请随时右上角联系我们的24/7代写客服。复杂网络Complex Network在网络理论的背景下,复杂网络是指具有非微观拓扑特征的图(网络)–这些特征在简单的网络(如格子或随机图)中不会出现,但在代表真实系统的网络中经常出现。复杂网络的研究是一个年轻而活跃的科学研究领域(自2000年以来),主要受到现实世界网络的经验发现的启发,如计算机网络、生物网络、技术网络、大脑网络、气候网络和社会网络。
复杂网络Complex Network大多数社会、生物和技术网络显示出实质性的非微观拓扑特征,其元素之间的连接模式既不是纯粹的规则也不是纯粹的随机。这些特征包括学位分布的重尾、高聚类系数、顶点之间的同态性或异态性、社区结构和层次结构。在有向网络的情况下,这些特征还包括互惠性、三联体重要性概况和其他特征。相比之下,过去研究的许多网络的数学模型,如格子和随机图,并没有显示这些特征。最复杂的结构可以由具有中等数量相互作用的网络实现。这与中等概率获得最大信息含量(熵)的事实相对应。
复杂网络Complex Network代写,免费提交作业要求, 满意后付款,成绩80\%以下全额退款,安全省心无顾虑。专业硕 博写手团队,所有订单可靠准时,保证 100% 原创。最高质量的复杂网络Complex Network作业代写,服务覆盖北美、欧洲、澳洲等 国家。 在代写价格方面,考虑到同学们的经济条件,在保障代写质量的前提下,我们为客户提供最合理的价格。 由于作业种类很多,同时其中的大部分作业在字数上都没有具体要求,因此复杂网络Complex Network作业代写的价格不固定。通常在专家查看完作业要求之后会给出报价。作业难度和截止日期对价格也有很大的影响。
同学们在留学期间,都对各式各样的作业考试很是头疼,如果你无从下手,不如考虑my-assignmentexpert™!
my-assignmentexpert™提供最专业的一站式服务:Essay代写,Dissertation代写,Assignment代写,Paper代写,Proposal代写,Proposal代写,Literature Review代写,Online Course,Exam代考等等。my-assignmentexpert™专注为留学生提供Essay代写服务,拥有各个专业的博硕教师团队帮您代写,免费修改及辅导,保证成果完成的效率和质量。同时有多家检测平台帐号,包括Turnitin高级账户,检测论文不会留痕,写好后检测修改,放心可靠,经得起任何考验!
想知道您作业确定的价格吗? 免费下单以相关学科的专家能了解具体的要求之后在1-3个小时就提出价格。专家的 报价比上列的价格能便宜好几倍。
数据科学代写|复杂网络代写Complex Network代考|Classical and Community-Aware Centrality Measures
This study investigates ten classical centrality measures, of which five are local (Degree, Leverage, Laplacian, Diffusion Degree, and Maximum Neighborhood Component) and five are global (Betweenness, Closeness, Katz, PageRank, and Subgraph). Table 1 reports their definition. They are compared with seven community-aware measures introduced earlier and described in Table 2 . Table 3 quotes the fifty real-world networks used in the experiments. They are from various domains (animal, biological, collaboration, online/offline social networks, infrastructural, and miscellaneous). Since the community structure is sensitive to the community detection algorithm, Louvain and Infomap are used to extract intra-community and inter-community links. Due to space constraints, the networks’ topological characteristics and results based on Louvain are provided in the supplementary materials ${ }^1$. Furthermore, as there are no fundamental differences, we restrict our attention in analyzing the results based on the community structure revealed using Infomap.
Correlation Analysis
The first investigation concerns how classical and community-aware centrality measures correlate for a given network. So, for each of the fifty networks, the Kendall’s Tau correlation is computed for all possible combinations between the ten classical $\left(\alpha_i\right)$ and seven community-aware centrality measures $\left(\beta_j\right)$. Figure 1 shows the distributions of the correlation values for each network. There is no Table 1. Definitions of classical centrality measures $(\alpha(i)) . a_{i, j}$ denotes the connectivity of a node $i$ to node $j$ from the adjacency matrix $A$. $N$ is the total number of nodes. $k_i$ and $k_j$ are the degrees of nodes $i$ and $j$, respectively. $\mathcal{N}1(i)$ is the set of direct neighbors of node $i . \varpi_i$ and $\varpi_j$ are the propagation probabilities of nodes $i$ and nodes $j$, respectively ( $\varpi$ is set to 1 for all nodes in this study). $\sigma(s, t)$ is the number of shortest paths between nodes $s$ and $t$ and $\sigma_i(s, t)$ is the number of shortest paths between nodes $s$ and $t$ that pass through node $i . d(i, j)$ is the shortest-path distance between node $i$ and $j . a{i j}^p$ is the connectivity of node $i$ with respect to all the other nodes at a given order of the adjacency matrix $A^p . s^p$ is the attenuation factor where $s \in[0,1]$. $\alpha_p(i)$ and $\alpha_p(j)$ are the PageRank centralities of node $i$ and node $j$, respectively. $d$ is the damping parameter (set to 0.85 in this study). $v_j$ refers to an eigenvector of the adjacency matrix $A$, associated with its eigenvalue $\lambda_j$.
数据科学代写|复杂网络代写Complex Network代考|Network Topology Analysis
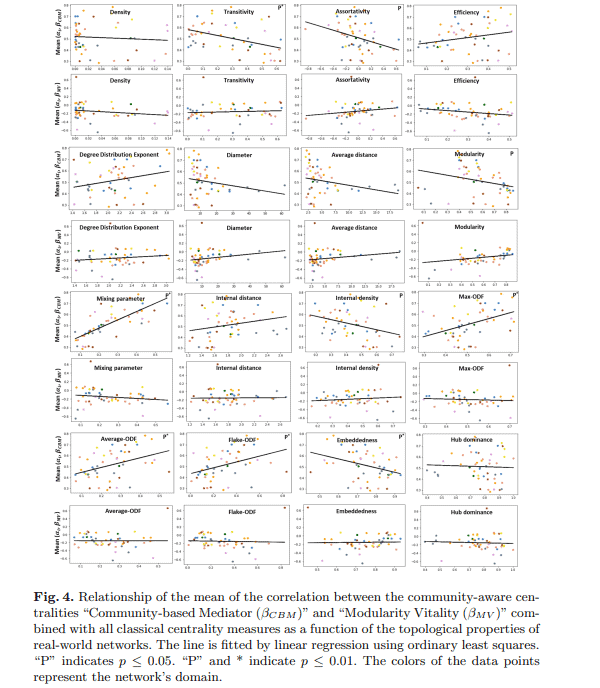
Correlation values between classical and community-aware centrality measures of each network are further processed. For a given network, each community-aware centrality measure is reduced to the mean value of the Kendall’s Tau correlation values computed for the ten classical centrality measures. Simple linear regression is performed to investigate the relationship with various topological properties of the networks. The average correlation values are the dependent variables, while the topological properties are the independent variables. The macroscopic features used are Density, Transitivity, Assortativity, Average distance, Diameter, Efficiency, and the Degree distribution exponent. The mesoscopic features used are Modularity, Mixing parameter, Internal distance, Internal density, MaxODF, Average-ODF, Flake-ODF, Embeddedness, and Hub dominance. If the $p$-value is below 0.05 , the dependent and independent variables’ relationship is considered statistically significant. Figure 4 presents the two extreme cases of statistical dependency between the mean and topological features. The premier case concerns Community-based Mediator (The mean value shows significant linear relationships with nine topological features). The last case is for Modularity Vitality (the mean value shows no meaningful linear relationship with any topological property). The remaining figures and linear regression parameters estimate for each community-aware centrality measure are provided in the supplementary materials.
Regarding macroscopic topological properties, we observe three situations. Network characteristics exhibit a significant linear relationship with the mean of either three, two, or none community-aware centrality. In that sense, transitivity and efficiency are the most influential macroscopic topological features. They show significant relationships with the mean of three different communityaware centrality measures. Then come density, assortativity, diameter, and average distance that affect two community-aware centrality measures. Finally, the degree distribution exponent is the only topological feature among the macroscopic features that do not show any significant relationship. Transitivity has a significant negative association with the mean of Community-Based Mediator $\left(\beta_{C B M}\right)$ and Participation Coefficient $\left(\beta_{P C}\right)$. Indeed, increasing transitivity leads to more triangles in the network. As Community-Based Mediator is based on the entropy of the intra-community and inter-community links of a node, transitivity may increase the difference between the two, resulting in a lower correlation. As the Participation Coefficient also exploits the margin of the proportion of the inter-community and intra-community links, it behaves similarly. One observes a positive association with transitivity for Community-based Centrality $\left(\beta_{C B C}\right)$. If the whole network forms a single community, $\beta_{C B C}$ reduces to degree centrality [22]. Consequently, the correlation between $\beta_{C B C}$ and classical measures tend to increase as transitivity increases. Efficiency has a significant positive association on Comm Centrality $\left(\beta_{C o m m}\right)$, Community-based Centrality $\left(\beta_{C B C}\right)$, and K-shell with Community $\left(\beta_{k s}\right)$. An increase in efficiency means that the average shortest path distance in a network is getting smaller. In other words, the network is more efficient when nodes are closely connected. Therefore, community-aware centrality measures tend to be more correlated with classical ones. Density has a significant positive association with Comm Centrality $\left(\beta_{C o m m}\right)$ and Community-based Centrality $\left(\beta_{C B C}\right)$. An increase in density means more links between nodes. Accordingly, $\beta_{C o m m}$ and $\beta_{C B C}$ get more analogous to classical centrality measures. Assortativity has a significant negative association with the mean of Community-Based Mediator $\left(\beta_{C B M}\right)$ and Participation Coefficient $\left(\beta_{P C}\right)$. An increase in assortativity means that there are more interactions between peers in the networks. It may also increase the margin of difference between intra-community and intercommunity links. Assortative networks tend to form communities with “similar” degree nodes. Consequently, intra-community and inter-community link densities may further differ from one community to another. Hence, a lower correlation between $\beta_{C B M} / \beta_{P C}$ and classical centrality measures is observed. Diameter and average distance have both a significant negative association with the mean of Community-based Centrality $\left(\beta_{C B C}\right)$ and K-shell with Community $\left(\beta_{k s}\right)$. An increase in both measures means that nodes are more distant from each other. These two community-aware centrality measures are the most sensitive to distance-related measures.

复杂网络代写
数据科学代写|复杂网络代写Complex Network代考|Classical and Community-Aware Centrality Measures
本研究研究了十个经典的中心性度量,其中五个是局部的(度、杠杆、拉普拉斯、扩散度和最大邻域分量),五个是全局的(between、Closeness、Katz、PageRank和Subgraph)。表1报告了它们的定义。将它们与前面介绍并在表2中描述的七项社区意识措施进行比较。表3引用了实验中使用的50个真实网络。它们来自不同的领域(动物、生物、协作、在线/离线社会网络、基础设施和其他领域)。由于社区结构对社区检测算法比较敏感,我们使用Louvain和Infomap来提取社区内和社区间的链接。由于篇幅限制,网络的拓扑特征和基于Louvain的结果在补充资料${ }^1$中给出。此外,由于没有根本差异,我们限制了对基于Infomap揭示的社区结构的结果进行分析的注意力。
相关分析
第一项调查关注的是经典和社区意识中心性测量在给定网络中是如何相互关联的。因此,对于50个网络中的每一个,Kendall’s Tau相关性被计算为10个经典$\left(\alpha_i\right)$和7个社区意识中心性测量$\left(\beta_j\right)$之间所有可能的组合。图1显示了每个网络的相关值分布。没有表1。经典中心性度量的定义$(\alpha(i)) . a_{i, j}$表示邻接矩阵$A$中节点$i$到节点$j$的连通性。$N$为节点总数。$k_i$和$k_j$分别为$i$和$j$节点的度数。$\mathcal{N}1(i)$为节点$i . \varpi_i$的直接邻居集合,$\varpi_j$分别为节点$i$和节点$j$的传播概率(本研究中所有节点均将$\varpi$设为1)。$\sigma(s, t)$是节点$s$和$t$之间的最短路径数,$\sigma_i(s, t)$是节点$s$和$t$之间通过节点$i . d(i, j)$的最短路径数,是节点$i$和$j . a{i j}^p$之间的最短路径距离,是节点$i$相对于所有其他节点在给定邻接矩阵阶数上的连度,$A^p . s^p$是衰减因子在哪里$s \in[0,1]$。$\alpha_p(i)$和$\alpha_p(j)$分别是节点$i$和节点$j$的PageRank中心性。$d$为阻尼参数(本研究设为0.85)。$v_j$为邻接矩阵$A$的特征向量,与其特征值$\lambda_j$相关联。
数据科学代写|复杂网络代写Complex Network代考|Network Topology Analysis
进一步处理各网络的经典中心性测度与社区意识中心性测度之间的相关值。对于给定的网络,每个社区意识的中心性度量被简化为十个经典中心性度量计算的肯德尔Tau相关值的平均值。简单的线性回归研究了网络的各种拓扑性质之间的关系。平均相关值是因变量,而拓扑属性是自变量。使用的宏观特征是密度、传递性、协调性、平均距离、直径、效率和度分布指数。使用的介观特征是模块化、混合参数、内部距离、内部密度、MaxODF、Average-ODF、Flake-ODF、Embeddedness和Hub dominance。如果p值小于0.05,则认为因变量和自变量的关系具有统计学意义。图4给出了均值和拓扑特征之间统计依赖的两个极端情况。最主要的案例是基于社区的中介(其平均值与9个拓扑特征表现出显著的线性关系)。最后一种情况是模块化活力(平均值显示与任何拓扑属性没有有意义的线性关系)。每个社区意识中心性测量的剩余数据和线性回归参数估计值在补充材料中提供。
关于宏观拓扑性质,我们观察到三种情况。网络特征与三个、两个或没有社区意识中心性的平均值表现出显著的线性关系。从这个意义上说,传递性和效率是最具影响力的宏观拓扑特征。它们与三种不同的社区意识中心性测量的平均值显示出显著的关系。然后是密度、协调性、直径和平均距离,它们会影响两个社区意识的中心性度量。最后,度分布指数是宏观特征中唯一不表现出任何显著关系的拓扑特征。传递性与社区中介平均值$\left(\beta_{C B M}\right)$和参与系数$\left(\beta_{P C}\right)$呈显著负相关。事实上,传递性的增加会导致网络中出现更多的三角形。基于社区的中介基于一个节点的社区内和社区间链路的熵,传递性可能会增加两者之间的差异,导致相关性降低。由于参与系数也利用了社区间联系和社区内联系所占比例的边际,因此其表现与此类似。我们观察到社区中心性与传递性呈正相关$\left(\beta_{C B C}\right)$。如果整个网络形成一个单一的社区,$\beta_{C B C}$降低为中心性度[22]。因此,$\beta_{C B C}$与经典测度之间的相关性随着传递性的增加而增加。效率与社区中心性$\left(\beta_{C o m m}\right)$、社区中心性$\left(\beta_{C B C}\right)$、K-shell与社区中心性$\left(\beta_{k s}\right)$呈显著正相关。效率的提高意味着网络中的平均最短路径距离越来越小。换句话说,当节点紧密连接时,网络效率更高。因此,社区意识中心性测度与经典测度的相关性更强。人口密度与社区中心性$\left(\beta_{C o m m}\right)$和社区中心性$\left(\beta_{C B C}\right)$呈显著正相关。密度的增加意味着节点之间的连接更多。因此,$\beta_{C o m m}$和$\beta_{C B C}$更类似于经典的中心性度量。分类性与社区中介的平均值$\left(\beta_{C B M}\right)$和参与系数$\left(\beta_{P C}\right)$呈显著负相关。协调性的增加意味着网络中的同伴之间有更多的互动。它还可能增加社区内和社区间联系之间的差距。分类网络倾向于形成具有“相似”度节点的社区。因此,群落内和群落间的联系密度可能进一步因群落而异。因此,观察到$\beta_{C B M} / \beta_{P C}$与经典中心性度量之间的相关性较低。直径和平均距离与社区中心性平均值$\left(\beta_{C B C}\right)$呈显著负相关,K-shell与社区中心性平均值$\left(\beta_{k s}\right)$呈显著负相关。两项指标的增加意味着节点之间的距离更远。这两个社区意识中心性指标对距离相关指标最为敏感。

数据科学代写|复杂网络代写Complex Network代考 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。
微观经济学代写
微观经济学是主流经济学的一个分支,研究个人和企业在做出有关稀缺资源分配的决策时的行为以及这些个人和企业之间的相互作用。my-assignmentexpert™ 为您的留学生涯保驾护航 在数学Mathematics作业代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的数学Mathematics代写服务。我们的专家在图论代写Graph Theory代写方面经验极为丰富,各种图论代写Graph Theory相关的作业也就用不着 说。
线性代数代写
线性代数是数学的一个分支,涉及线性方程,如:线性图,如:以及它们在向量空间和通过矩阵的表示。线性代数是几乎所有数学领域的核心。
博弈论代写
现代博弈论始于约翰-冯-诺伊曼(John von Neumann)提出的两人零和博弈中的混合策略均衡的观点及其证明。冯-诺依曼的原始证明使用了关于连续映射到紧凑凸集的布劳威尔定点定理,这成为博弈论和数学经济学的标准方法。在他的论文之后,1944年,他与奥斯卡-莫根斯特恩(Oskar Morgenstern)共同撰写了《游戏和经济行为理论》一书,该书考虑了几个参与者的合作游戏。这本书的第二版提供了预期效用的公理理论,使数理统计学家和经济学家能够处理不确定性下的决策。
微积分代写
微积分,最初被称为无穷小微积分或 “无穷小的微积分”,是对连续变化的数学研究,就像几何学是对形状的研究,而代数是对算术运算的概括研究一样。
它有两个主要分支,微分和积分;微分涉及瞬时变化率和曲线的斜率,而积分涉及数量的累积,以及曲线下或曲线之间的面积。这两个分支通过微积分的基本定理相互联系,它们利用了无限序列和无限级数收敛到一个明确定义的极限的基本概念 。
计量经济学代写
什么是计量经济学?
计量经济学是统计学和数学模型的定量应用,使用数据来发展理论或测试经济学中的现有假设,并根据历史数据预测未来趋势。它对现实世界的数据进行统计试验,然后将结果与被测试的理论进行比较和对比。
根据你是对测试现有理论感兴趣,还是对利用现有数据在这些观察的基础上提出新的假设感兴趣,计量经济学可以细分为两大类:理论和应用。那些经常从事这种实践的人通常被称为计量经济学家。
Matlab代写
MATLAB 是一种用于技术计算的高性能语言。它将计算、可视化和编程集成在一个易于使用的环境中,其中问题和解决方案以熟悉的数学符号表示。典型用途包括:数学和计算算法开发建模、仿真和原型制作数据分析、探索和可视化科学和工程图形应用程序开发,包括图形用户界面构建MATLAB 是一个交互式系统,其基本数据元素是一个不需要维度的数组。这使您可以解决许多技术计算问题,尤其是那些具有矩阵和向量公式的问题,而只需用 C 或 Fortran 等标量非交互式语言编写程序所需的时间的一小部分。MATLAB 名称代表矩阵实验室。MATLAB 最初的编写目的是提供对由 LINPACK 和 EISPACK 项目开发的矩阵软件的轻松访问,这两个项目共同代表了矩阵计算软件的最新技术。MATLAB 经过多年的发展,得到了许多用户的投入。在大学环境中,它是数学、工程和科学入门和高级课程的标准教学工具。在工业领域,MATLAB 是高效研究、开发和分析的首选工具。MATLAB 具有一系列称为工具箱的特定于应用程序的解决方案。对于大多数 MATLAB 用户来说非常重要,工具箱允许您学习和应用专业技术。工具箱是 MATLAB 函数(M 文件)的综合集合,可扩展 MATLAB 环境以解决特定类别的问题。可用工具箱的领域包括信号处理、控制系统、神经网络、模糊逻辑、小波、仿真等。