如果你也在 怎样代写量子力学Quantum mechanics这个学科遇到相关的难题,请随时右上角联系我们的24/7代写客服。量子力学Quantum mechanics在理论物理学中,量子场论(QFT)是一个结合了经典场论、狭义相对论和量子力学的理论框架。QFT在粒子物理学中用于构建亚原子粒子的物理模型,在凝聚态物理学中用于构建准粒子的模型。
量子力学Quantum mechanics产生于跨越20世纪大部分时间的几代理论物理学家的工作。它的发展始于20世纪20年代对光和电子之间相互作用的描述,最终形成了第一个量子场理论–量子电动力学。随着微扰计算中各种无限性的出现和持续存在,一个主要的理论障碍很快出现了,这个问题直到20世纪50年代随着重正化程序的发明才得以解决。第二个主要障碍是QFT显然无法描述弱相互作用和强相互作用,以至于一些理论家呼吁放弃场论方法。20世纪70年代,规整理论的发展和标准模型的完成导致了量子场论的复兴。
量子力学Quantum mechanics代写,免费提交作业要求, 满意后付款,成绩80\%以下全额退款,安全省心无顾虑。专业硕 博写手团队,所有订单可靠准时,保证 100% 原创。最高质量的量子力学Quantum mechanics作业代写,服务覆盖北美、欧洲、澳洲等 国家。 在代写价格方面,考虑到同学们的经济条件,在保障代写质量的前提下,我们为客户提供最合理的价格。 由于作业种类很多,同时其中的大部分作业在字数上都没有具体要求,因此量子力学Quantum mechanics作业代写的价格不固定。通常在专家查看完作业要求之后会给出报价。作业难度和截止日期对价格也有很大的影响。
同学们在留学期间,都对各式各样的作业考试很是头疼,如果你无从下手,不如考虑my-assignmentexpert™!
my-assignmentexpert™提供最专业的一站式服务:Essay代写,Dissertation代写,Assignment代写,Paper代写,Proposal代写,Proposal代写,Literature Review代写,Online Course,Exam代考等等。my-assignmentexpert™专注为留学生提供Essay代写服务,拥有各个专业的博硕教师团队帮您代写,免费修改及辅导,保证成果完成的效率和质量。同时有多家检测平台帐号,包括Turnitin高级账户,检测论文不会留痕,写好后检测修改,放心可靠,经得起任何考验!
想知道您作业确定的价格吗? 免费下单以相关学科的专家能了解具体的要求之后在1-3个小时就提出价格。专家的 报价比上列的价格能便宜好几倍。
我们在物理Physical代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的物理Physical代写服务。我们的专家在量子力学Quantum mechanics代写方面经验极为丰富,各种量子力学Quantum mechanics相关的作业也就用不着说。
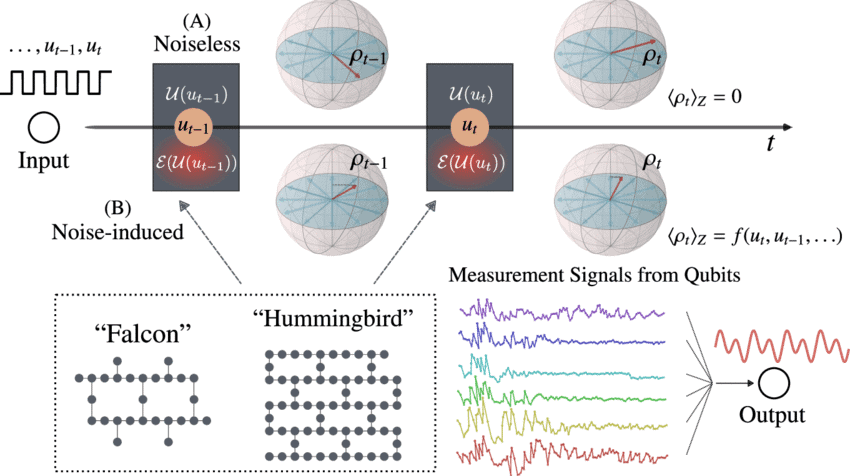
物理代写|量子力学代写Quantum mechanics代考|Noisy Evolution from a Random Unitary
Perhaps the simplest example of a quantum channel is the quantum bit-flip channel, which has the following action on a qubit density operator $\rho$ :
$$
p X \rho X^{\dagger}+(1-p) \rho .
$$
The above density operator is more “mixed” than the original density operator and we will make this statement more precise in Chapter 10, when we study entropy. The evolution $\rho \rightarrow p X \rho X^{\dagger}+(1-p) \rho$ is clearly a legitimate quantum channel. Here the Kraus operators are ${\sqrt{p} X, \sqrt{1-p} I}$ and it is clear that they satisfy the completeness relation.
A generalization of the above discussion is to consider some ensemble of unitaries (a random unitary) $\left{p(k), U_k\right}$ that we can apply to a density operator $\rho$, resulting in the following output density operator:
$$
\sum_k p(k) U_k \rho U_k^{\dagger}
$$
Dephasing Channels
We have already given the example of a noisy quantum bit-flip channel in Section 4.7.1. Another important example is a bit flip in the conjugate basis, or equivalently, a phase-flip channel. This channel acts as follows on any given density operator:
$$
\rho \rightarrow(1-p) \rho+p Z \rho Z
$$
It is also known as a dephasing channel.
For $p=1 / 2$, the action of the dephasing channel on a given quantum state is equivalent to the action of measuring the qubit in the computational basis and forgetting the result of the measurement. We make this idea more clear with an example. First, suppose that we have a qubit
$$
|\psi\rangle=\alpha|0\rangle+\beta|1\rangle
$$
and we measure it in the computational basis. Then the postulates of quantum theory state that the qubit becomes $|0\rangle$ with probability $|\alpha|^2$ and it becomes $|1\rangle$ with probability $|\beta|^2$. Suppose that we forget the measurement outcome, or alternatively, that we do not have access to it. Then our best description of the qubit is with the following ensemble:
$$
\left{\left{|\alpha|^2,|0\rangle\right},\left{|\beta|^2,|1\rangle\right}\right}
$$
The density operator of this ensemble is
$$
|\alpha|^2|0\rangle\left\langle\left. 0|+| \beta\right|^2 \mid 1\right\rangle\langle 1|
$$
物理代写|量子力学代写Quantum mechanics代考|Pauli Channels
A Pauli channel is a generalization of the above dephasing channel and the bitflip channel. It simply applies a random Pauli operator according to a probability distribution. The map for a qubit Pauli channel is
$$
\rho \rightarrow \sum_{i, j=0}^1 p(i, j) Z^i X^j \rho X^j Z^i .
$$
The generalization of this channel to qudits is straightforward. We simply replace the Pauli operators with the Heisenberg-Weyl operators. The Pauli qudit channel is
$$
\rho \rightarrow \sum_{i, j=0}^{d-1} p(i, j) Z(i) X(j) \rho X^{\dagger}(j) Z^{\dagger}(i) .
$$
These channels have been prominent in the study of quantum key distribution.
EXercise 4.7.2 We can write a Pauli channel as
$$
\rho \rightarrow p_I \rho+p_X X \rho X+p_Y Y \rho Y+p_Z Z \rho Z .
$$
Verify that the action of the Pauli channel on the Bloch vector is
$$
\begin{aligned}
& \left(r_x, r_y, r_z\right) \rightarrow \
& \left(\left(p_I+p_X-p_Y-p_Z\right) r_x,\left(p_I+p_Y-p_X-p_Z\right) r_y,\left(p_I+p_Z-p_X-p_Y\right) r_z\right) .
\end{aligned}
$$
量子力学代写
物理代写|量子力学代写Quantum mechanics代考|Noisy Evolution from a Random Unitary
也许量子通道最简单的例子是量子比特翻转通道,它对量子比特密度算子$\rho$有以下作用:
$$
p X \rho X^{\dagger}+(1-p) \rho .
$$
上述密度算符比原来的密度算符更“混合”,我们将在第10章学习熵时更精确地说明这一点。进化$\rho \rightarrow p X \rho X^{\dagger}+(1-p) \rho$显然是一个合法的量子通道。这里Kraus算子是${\sqrt{p} X, \sqrt{1-p} I}$,很明显它们满足完备关系。
上述讨论的推广是考虑一些一元集合(随机一元)$\left{p(k), U_k\right}$,我们可以将其应用于密度算子$\rho$,从而得到以下输出密度算子:
$$
\sum_k p(k) U_k \rho U_k^{\dagger}
$$
消相通道
我们已经在第4.7.1节中给出了噪声量子比特翻转信道的例子。另一个重要的例子是共轭基中的位翻转,或者等价地,相位翻转通道。对于任何给定的密度算子,该通道的作用如下:
$$
\rho \rightarrow(1-p) \rho+p Z \rho Z
$$
它也被称为减相通道。
对于$p=1 / 2$,脱相通道对给定量子态的作用相当于在计算基中测量量子位元并忘记测量结果的作用。我们用一个例子来说明这个观点。首先,假设我们有一个量子位
$$
|\psi\rangle=\alpha|0\rangle+\beta|1\rangle
$$
我们在计算基础上测量它。然后,量子理论的假设表明,量子比特变成$|0\rangle$的概率为$|\alpha|^2$,它变成$|1\rangle$的概率为$|\beta|^2$。假设我们忘记了测量结果,或者我们没有访问它的权限。那么我们对量子比特的最佳描述是以下集合:
$$
\left{\left{|\alpha|^2,|0\rangle\right},\left{|\beta|^2,|1\rangle\right}\right}
$$
这个集合的密度算符是
$$
|\alpha|^2|0\rangle\left\langle\left. 0|+| \beta\right|^2 \mid 1\right\rangle\langle 1|
$$
物理代写|量子力学代写Quantum mechanics代考|Pauli Channels
泡利信道是上述消相信道和位翻转信道的泛化。它只是根据概率分布应用一个随机泡利算子。量子比特泡利信道的映射是
$$
\rho \rightarrow \sum_{i, j=0}^1 p(i, j) Z^i X^j \rho X^j Z^i .
$$
将这个通道推广到量值是很简单的。我们简单地用海森堡-魏尔算子代替泡利算子。泡利quit频道是
$$
\rho \rightarrow \sum_{i, j=0}^{d-1} p(i, j) Z(i) X(j) \rho X^{\dagger}(j) Z^{\dagger}(i) .
$$
这些信道在量子密钥分发的研究中一直很突出。
可以将泡利通道写成
$$
\rho \rightarrow p_I \rho+p_X X \rho X+p_Y Y \rho Y+p_Z Z \rho Z .
$$
验证泡利通道对布洛赫矢量的作用是
$$
\begin{aligned}
& \left(r_x, r_y, r_z\right) \rightarrow \
& \left(\left(p_I+p_X-p_Y-p_Z\right) r_x,\left(p_I+p_Y-p_X-p_Z\right) r_y,\left(p_I+p_Z-p_X-p_Y\right) r_z\right) .
\end{aligned}
$$

物理代写|量子力学代写Quantum mechanics代考 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。