如果你也在 怎样代写统计推断Statistical Inference 这个学科遇到相关的难题，请随时右上角联系我们的24/7代写客服。统计推断Statistical Inference领域，有两种主要的思想流派。每一种方法都有其支持者，但人们普遍认为，在入门课程中涵盖的所有问题上，这两种方法都是有效的，并且在应用于实际问题时得到相同的数值。传统课程只涉及其中一种方法，这使得学生无法接触到统计推断的整个领域。传统的方法，也被称为频率论或正统观点，几乎直接导致了上面的问题。另一种方法，也称为概率论作为逻辑${}^1$，直接从概率论导出所有统计推断。

统计推断Statistical Inference指的是一个研究领域，我们在面对不确定性的情况下，根据我们观察到的数据，试图推断世界的未知特性。它是一个数学框架，在许多情况下量化我们的常识所说的话，但在常识不够的情况下，它允许我们超越常识。对正确的统计推断的无知会导致错误的决策和浪费金钱。就像对其他领域的无知一样，对统计推断的无知也会让别人操纵你，让你相信一些错误的事情是正确的。

统计推断Statistical Inference代写，免费提交作业要求， 满意后付款，成绩80\%以下全额退款，安全省心无顾虑。专业硕 博写手团队，所有订单可靠准时，保证 100% 原创。最高质量的统计推断Statistical Inference作业代写，服务覆盖北美、欧洲、澳洲等 国家。 在代写价格方面，考虑到同学们的经济条件，在保障代写质量的前提下，我们为客户提供最合理的价格。 由于作业种类很多，同时其中的大部分作业在字数上都没有具体要求，因此统计推断Statistical Inference作业代写的价格不固定。通常在专家查看完作业要求之后会给出报价。作业难度和截止日期对价格也有很大的影响。

同学们在留学期间，都对各式各样的作业考试很是头疼，如果你无从下手，不如考虑my-assignmentexpert™！

my-assignmentexpert™提供最专业的一站式服务：Essay代写，Dissertation代写，Assignment代写，Paper代写，Proposal代写，Proposal代写，Literature Review代写，Online Course，Exam代考等等。my-assignmentexpert™专注为留学生提供Essay代写服务，拥有各个专业的博硕教师团队帮您代写，免费修改及辅导，保证成果完成的效率和质量。同时有多家检测平台帐号，包括Turnitin高级账户，检测论文不会留痕，写好后检测修改，放心可靠，经得起任何考验！

统计代写|统计推断代考Statistical Inference代写|Some Motivating Examples

In a certain state of the Union, $n$ landfills are classified according to their concentration of three hazardous chemicals: arsenic, barium, and mercury. Suppose that the concentration of each one of the three chemicals is characterized as either high or low. Then some of the questions which can be posed are as follows: (i) If a landfill is chosen at random from among the $n$, what is the probability it is of a specific configuration? In particular, what is the probability that it has: (a) High concentration of barium? (b) High concentration of mercury and low concentration of both arsenic and barium? (c) High concentration of any two of the chemicals and low concentration of the third?
(d) High concentration of any one of the chemicals and low concentration of the other two? (ii) How can one check whether the proportions of the landfills falling into each one of the eight possible configurations (regarding the levels of concentration) agree with a priori stipulated numbers?

Suppose a disease is present in $100 p_1 \%\left(0<p_1<1\right)$ of a population. A diagnostic test is available but is yet to be perfected. The test shows $100 p_2 \%$ false positives $\left(0<p_2<1\right)$ and $100 p_3 \%$ false negatives $\left(0<p_3<1\right)$. That is, for a patient not having the disease, the test shows positive (+) with probability $p_2$ and negative (-) with probability $1-p_2$. For a patient having the disease, the test shows “-” with probability $p_3$ and “+” with probability $1-p_3$. A person is chosen at random from the target population, and let $D$ be the event that the person is diseased and $N$ be the event that the person is not diseased. Then, it is clear that some important questions are as follows: In terms of $p_1, p_2$, and $p_3$ : (i) Determine the probabilities of the following configurations: $D$ and + , $D$ and,$- N$ and,$+ N$ and – . (ii) Also, determine the probability that a person will test + or the probability the person will test -. (iii) If the person chosen tests + , what is the probability that he/she is diseased? What is the probability that he/she is diseased, if the person tests -?

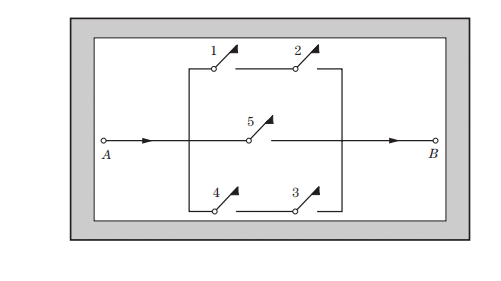
In the circuit drawn below, suppose that switch $i=1, \ldots, 5$ turns on with probability $p_i$ and independently of the remaining switches. What is the probability of having current transferred from point A to point B?

统计代写|统计推断代考Statistical Inference代写|Some Fundamental Concepts

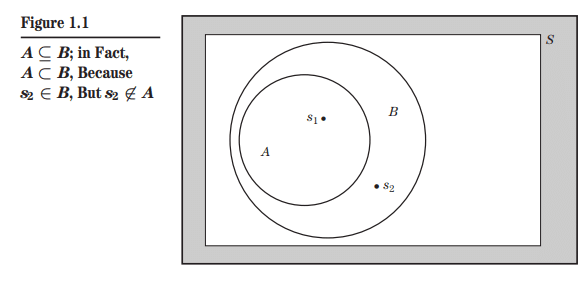
One of the most basic concepts in probability and statistics is that of a random experiment. Although a more precise definition is possible, we will restrict ourselves here to understanding a random experiment as a procedure which is carried out under a certain set of conditions; it can be repeated any number of times under the same set of conditions, and upon the completion of the procedure certain results are observed. The results obtained are denoted by $s$ and are called sample points. The set of all possible sample points is denoted by $\mathcal{S}$ and is called a sample space. Subsets of $\mathcal{S}$ are called events and are denoted by capital letters A, B, C, etc. An event consisting of one sample point only, ${s}$, is called a simple event and composite otherwise. An event A occurs (or happens) if the outcome of the random experiment (that is, the sample point $s$ ) belongs in $A, s \in A ; A$ does not occur (or does not happen) if $s \notin A$. The event $\mathcal{S}$ always occurs and is called the sure or certain event. On the other hand, the event $\emptyset$ never happens and is called the impossible event. Of course, the relation $A \subseteq B$ between two events $A$ and $B$ means that the event $B$ occurs whenever $A$ does, but not necessarily the opposite. (See Figure 1.1 for the Venn diagram depicting the relation $A \subseteq B$.) The events $A$ and $B$ are equal if both $A \subseteq B$ and $B \subseteq A$.

Some random experiments are given in the following along with corresponding sample spaces and some events.

Tossing three distinct coins once.
Then, with $H$ and $T$ standing for “heads” and “tails,” respectively, a sample space is:
$$
\mathcal{S}={H H H, H H T, H T H, T H H, H T T, T H T, T T H, T T T} .
$$
The event $A=$ “no more than $1 H$ occurs” is given by:
$$
A={T T T, H T T, T H T, T T H} .
$$
Rolling once two distinct dice.
Then a sample space is:
$$
\mathcal{S}={(1,1),(1,2), \ldots,(1,6), \ldots,(6,1),(6,2), \ldots,(6,6)},
$$
and the event $B=$ “the sum of numbers on the upper faces is $\leq 5$ ” is:
$$
B={(1,1),(1,2),(1,3),(1,4),(2,1),(2,2),(2,3),(3,1),(3,2),(4,1)} .
$$
Drawing a card from a well-shuffled standard deck of 52 cards. Denoting by $C, D, H$, and $S$ clubs, diamonds, hearts, and spades, respectively, by $J, Q, K$ Jack, Queen, and King, and using 1 for aces, the sample space is given by:
$$
\mathcal{S}=\left{1_C, \ldots, 1_S, \ldots, 10_C, \ldots, 10_S, \ldots, K_C, \ldots, K_S\right} .
$$
An event $A$ may be described by: $A=$ “red and face card,” so that
$$
A=\left{J_D, J_H, Q_D, Q_H, K_D, K_H\right} .
$$

统计推断代写

统计代写|统计推断代考Statistical Inference代写|Some Motivating Examples

在美国的某个州，$n$垃圾填埋场按照三种有害化学物质的浓度进行分类:砷、钡和汞。假设这三种化学物质中的每一种的浓度都表现为高或低。然后可以提出以下一些问题:(i)如果从$n$中随机选择一个垃圾填埋场，它具有特定配置的概率是多少?特别是，它有:(a)高浓度钡的概率是多少?(b)汞浓度高，砷和钡浓度低?(c)其中任何两种化学品浓度高，而第三种化学品浓度低?
(d)其中任何一种化学品浓度高而其他两种浓度低?(ii)如何核对八种可能的堆填区结构(就浓度水平而言)中每一种的比例是否与预先规定的数字相符?

假设一种疾病出现在人群的$100 p_1 \%\left(0<p_1<1\right)$中。一种诊断测试是可用的，但还有待完善。测试显示$100 p_2 \%$假阳性$\left(0<p_2<1\right)$和$100 p_3 \%$假阴性$\left(0<p_3<1\right)$。也就是说，对于没有患病的患者，测试结果为阳性(+)的概率为$p_2$，为阴性(-)的概率为$1-p_2$。对于患有这种疾病的患者，测试显示“-”的概率为$p_3$，“+”的概率为$1-p_3$。从目标人群中随机选择一个人，设$D$为患病事件，$N$为未患病事件。那么，很明显，一些重要的问题如下:在$p_1, p_2$和$p_3$方面:(i)确定以下配置的概率:$D$和+，$D$和，$- N$和，$+ N$和-。(ii)同时，确定某人将测试+的概率或该人员将测试-的概率。(iii)如果被选中的人测试+，他/她患病的概率是多少?他/她患病的概率有多大?

在下面的电路中，假设开关$i=1, \ldots, 5$以$p_i$的概率打开，并且独立于其他开关。电流从A点传输到B点的概率是多少?

统计代写|统计推断代考Statistical Inference代写|Some Fundamental Concepts

概率论和统计学中最基本的概念之一是随机实验。虽然可能有一个更精确的定义，但我们在这里仅限于把随机实验理解为在一定条件下进行的过程;它可以在相同的条件下重复任意次数，并在程序完成后观察到某些结果。得到的结果用$s$表示，称为样本点。所有可能的样本点的集合用$\mathcal{S}$表示，称为样本空间。$\mathcal{S}$的子集称为事件，用大写字母A、B、C等表示。仅由一个样本点${s}$组成的事件称为简单事件，否则称为复合事件。如果属于$A, s \in A ; A$的随机实验结果(即样本点$s$)不发生(或不发生)，则事件A发生(或发生)，如果$s \notin A$。事件$\mathcal{S}$总是发生，被称为确定事件或确定事件。另一方面，事件$\emptyset$永远不会发生，被称为不可能的事件。当然，两个事件$A$和$B$之间的关系$A \subseteq B$意味着事件$B$在$A$发生时发生，但不一定相反。(图1.1为描述$A \subseteq B$关系的维恩图。)如果$A \subseteq B$和$B \subseteq A$同时存在，则事件$A$和$B$相等。

下面给出了一些随机实验，并给出了相应的样本空间和事件。

一次抛三枚不同的硬币。
然后，$H$和$T$分别代表“正面”和“反面”，则样本空间为:
$$
\mathcal{S}={H H H, H H T, H T H, T H H, H T T, T H T, T T H, T T T} .
$$
事件$A=$ “no more than $1 H$发生”由以下方式给出:
$$
A={T T T, H T T, T H T, T T H} .
$$
掷一次两个不同的骰子。
则样本空间为:
$$
\mathcal{S}={(1,1),(1,2), \ldots,(1,6), \ldots,(6,1),(6,2), \ldots,(6,6)},
$$
事件$B=$“上面面的数字之和为$\leq 5$”是:
$$
B={(1,1),(1,2),(1,3),(1,4),(2,1),(2,2),(2,3),(3,1),(3,2),(4,1)} .
$$
从一副52张洗牌的标准牌中抽一张牌。分别用$C, D, H$和$S$表示梅花、方块、红心和黑桃，用$J, Q, K$表示杰克、皇后和国王，用1表示a，样本空间由下式给出:
$$
\mathcal{S}=\left{1_C, \ldots, 1_S, \ldots, 10_C, \ldots, 10_S, \ldots, K_C, \ldots, K_S\right} .
$$
事件$A$可以描述为:$A=$“红脸牌”，因此
$$
A=\left{J_D, J_H, Q_D, Q_H, K_D, K_H\right} .
$$

统计代写|统计推断代考Statistical Inference代写 请认准exambang™. exambang™为您的留学生涯保驾护航。

微观经济学代写

微观经济学是主流经济学的一个分支，研究个人和企业在做出有关稀缺资源分配的决策时的行为以及这些个人和企业之间的相互作用。my-assignmentexpert™ 为您的留学生涯保驾护航 在数学Mathematics作业代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的数学Mathematics代写服务。我们的专家在图论代写Graph Theory代写方面经验极为丰富，各种图论代写Graph Theory相关的作业也就用不着 说。

线性代数代写

线性代数是数学的一个分支，涉及线性方程，如：线性图，如：以及它们在向量空间和通过矩阵的表示。线性代数是几乎所有数学领域的核心。

博弈论代写

现代博弈论始于约翰-冯-诺伊曼（John von Neumann）提出的两人零和博弈中的混合策略均衡的观点及其证明。冯-诺依曼的原始证明使用了关于连续映射到紧凑凸集的布劳威尔定点定理，这成为博弈论和数学经济学的标准方法。在他的论文之后，1944年，他与奥斯卡-莫根斯特恩（Oskar Morgenstern）共同撰写了《游戏和经济行为理论》一书，该书考虑了几个参与者的合作游戏。这本书的第二版提供了预期效用的公理理论，使数理统计学家和经济学家能够处理不确定性下的决策。

微积分代写

微积分，最初被称为无穷小微积分或 “无穷小的微积分”，是对连续变化的数学研究，就像几何学是对形状的研究，而代数是对算术运算的概括研究一样。

它有两个主要分支，微分和积分；微分涉及瞬时变化率和曲线的斜率，而积分涉及数量的累积，以及曲线下或曲线之间的面积。这两个分支通过微积分的基本定理相互联系，它们利用了无限序列和无限级数收敛到一个明确定义的极限的基本概念 。

计量经济学代写

什么是计量经济学？
计量经济学是统计学和数学模型的定量应用，使用数据来发展理论或测试经济学中的现有假设，并根据历史数据预测未来趋势。它对现实世界的数据进行统计试验，然后将结果与被测试的理论进行比较和对比。

根据你是对测试现有理论感兴趣，还是对利用现有数据在这些观察的基础上提出新的假设感兴趣，计量经济学可以细分为两大类：理论和应用。那些经常从事这种实践的人通常被称为计量经济学家。

Matlab代写

MATLAB 是一种用于技术计算的高性能语言。它将计算、可视化和编程集成在一个易于使用的环境中，其中问题和解决方案以熟悉的数学符号表示。典型用途包括：数学和计算算法开发建模、仿真和原型制作数据分析、探索和可视化科学和工程图形应用程序开发，包括图形用户界面构建MATLAB 是一个交互式系统，其基本数据元素是一个不需要维度的数组。这使您可以解决许多技术计算问题，尤其是那些具有矩阵和向量公式的问题，而只需用 C 或 Fortran 等标量非交互式语言编写程序所需的时间的一小部分。MATLAB 名称代表矩阵实验室。MATLAB 最初的编写目的是提供对由 LINPACK 和 EISPACK 项目开发的矩阵软件的轻松访问，这两个项目共同代表了矩阵计算软件的最新技术。MATLAB 经过多年的发展，得到了许多用户的投入。在大学环境中，它是数学、工程和科学入门和高级课程的标准教学工具。在工业领域，MATLAB 是高效研究、开发和分析的首选工具。MATLAB 具有一系列称为工具箱的特定于应用程序的解决方案。对于大多数 MATLAB 用户来说非常重要，工具箱允许您学习和应用专业技术。工具箱是 MATLAB 函数（M 文件）的综合集合，可扩展 MATLAB 环境以解决特定类别的问题。可用工具箱的领域包括信号处理、控制系统、神经网络、模糊逻辑、小波、仿真等。