MY-ASSIGNMENTEXPERT™可以为您提供 my.uq.edu.au EC309 Econometrics计量经济学的代写代考和辅导服务!
这是昆士兰大学计量经济学课程的代写成功案例。
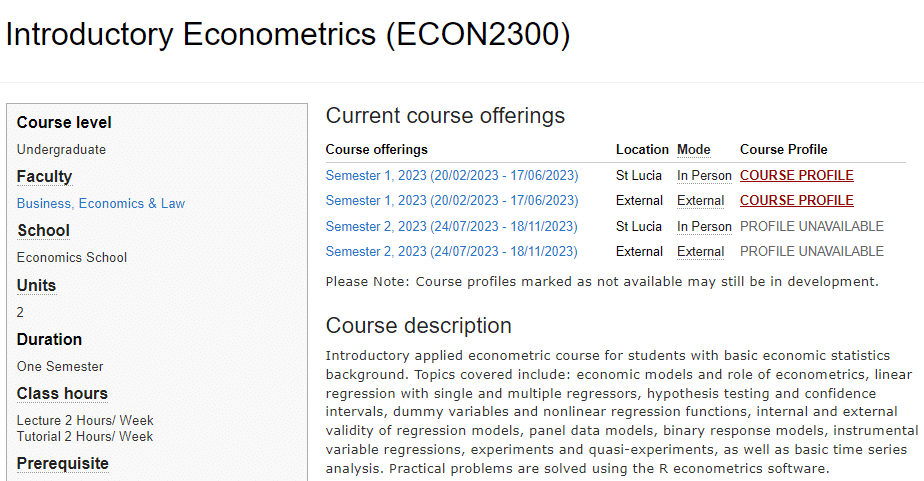
ECON2300课程简介
Course description
Introductory applied econometric course for students with basic economic statistics background. Topics covered include: economic models and role of econometrics, linear regression with single and multiple regressors, hypothesis testing and confidence intervals, dummy variables and nonlinear regression functions, internal and external validity of regression models, panel data models, binary response models, instrumental variable regressions, experiments and quasi-experiments, as well as basic time series analysis. Practical problems are solved using the R econometrics software.
Prerequisites
This is an introductory course in applied econometrics. It reviews and builds on the simple linear regression model taught in introductory statistics courses such as ECON1310 and ECON1320. The models studied in this course have numerous applications in economics, finance, marketing, management and related areas. A feature of the course is the way examples and exercises are drawn from these different discipline areas to illustrate the usefulness and limitations of certain econometric/statistical techniques. Hands-on experience in applying these techniques is gained through the use of R, an econometric computer software package available in the BEL computer laboratories.
ECON2300 Econometrics HELP(EXAM HELP, ONLINE TUTOR)
Exercise 2.19 Show (2.46)-(2.47), namely that for
$$
d(\boldsymbol{\beta})=\mathbb{E}\left[\left(m(\boldsymbol{x})-\boldsymbol{x}^{\prime} \boldsymbol{\beta}\right)^2\right]
$$
then
$$
\begin{aligned}
\boldsymbol{\beta} & =\underset{\boldsymbol{b} \in \mathbb{R}^k}{\operatorname{argmin}} d(\boldsymbol{b}) \
& =\left(\mathbb{E}\left[\boldsymbol{x} \boldsymbol{x}^{\prime}\right]\right)^{-1} \mathbb{E}[\boldsymbol{x} m(\boldsymbol{x})] \
& =\left(\mathbb{E}\left[\boldsymbol{x} \boldsymbol{x}^{\prime}\right]\right)^{-1} \mathbb{E}[\boldsymbol{x} y] .
\end{aligned}
$$
Hint: To show $\mathbb{E}[\boldsymbol{x} m(\boldsymbol{x})]=\mathbb{E}[\boldsymbol{x} y]$ use the law of iterated expectations.
Exercise 2.20 Verify that (2.54) holds with $m(\boldsymbol{x})$ defined in $(2.5)$ when $(y, \boldsymbol{x})$ have a joint density $f(y, \boldsymbol{x})$.
Exercise 2.21 Consider the short and long projections
$$
\begin{gathered}
y=x \gamma_1+e \
y=x \beta_1+x^2 \beta_2+u
\end{gathered}
$$
(a) Under what condition does $\gamma_1=\beta_1$ ?
(b) Now suppose the long projection is
$$
y=x \theta_1+x^3 \theta_2+v
$$
Is there a similar condition under which $\gamma_1=\theta_1$ ?
Exercise 2.22 Take the homoskedastic model
$$
\begin{aligned}
y & =\boldsymbol{x}_1^{\prime} \boldsymbol{\beta}_1+\boldsymbol{x}_2^{\prime} \boldsymbol{\beta}_2+e \
\mathbb{E}\left[e \mid \boldsymbol{x}_1, \boldsymbol{x}_2\right] & =0 \
\mathbb{E}\left[e^2 \mid \boldsymbol{x}_1, \boldsymbol{x}_2\right] & =\sigma^2 \
\mathbb{E}\left[\boldsymbol{x}_2 \mid \boldsymbol{x}_1\right] & =\boldsymbol{\Gamma} \boldsymbol{x}_1 \
\boldsymbol{\Gamma} & \neq 0 .
\end{aligned}
$$
Suppose the parameter $\boldsymbol{\beta}_1$ is of interest. We know that the exclusion of $\boldsymbol{x}_2$ creates omited variable bias in the projection coefficient on $\boldsymbol{x}_2$. It also changes the equation error. Our question is: what is the effect on the homoskedasticity property of the induced equation error? Does the exclusion of $\boldsymbol{x}_2$ induce heteroskedasticity or not? Be specific.
Exercise 3.1 Let $y$ be a random variable with $\mu=\mathbb{E}[y]$ and $\sigma^2=\operatorname{var}[y]$. Define
$$
g\left(y, \mu, \sigma^2\right)=\left(\begin{array}{c}
y-\mu \
(y-\mu)^2-\sigma^2
\end{array}\right) .
$$
Let $\left(\widehat{\mu}, \widehat{\sigma}^2\right)$ be the values such that $\bar{g}n\left(\widehat{\mu}, \widehat{\sigma}^2\right)=\mathbf{0}$ where $\bar{g}_n(m, s)=n^{-1} \sum{i=1}^n g\left(y_i, m, s\right)$. Show that $\widehat{\mu}$ and $\widehat{\sigma}^2$ are the sample mean and variance.
Exercise 3.2 Consider the OLS regression of the $n \times 1$ vector $\boldsymbol{y}$ on the $n \times k$ matrix $\boldsymbol{X}$. Consider an alternative set of regressors $\boldsymbol{Z}=\boldsymbol{X} \boldsymbol{C}$, where $\boldsymbol{C}$ is a $k \times k$ non-singular matrix. Thus, each column of $\boldsymbol{Z}$ is a mixture of some of the columns of $\boldsymbol{X}$. Compare the OLS estimates and residuals from the regression of $\boldsymbol{y}$ on $\boldsymbol{X}$ to the OLS estimates from the regression of $\boldsymbol{y}$ on $\boldsymbol{Z}$.

MY-ASSIGNMENTEXPERT™可以为您提供 MY.UQ.EDU.AU EC309 ECONOMETRICS计量经济学的代写代考和辅导服务