MY-ASSIGNMENTEXPERT™可以为您提供mathstat MATH2300 Mathematical Modeling数学建模的代写代考和辅导服务!
这是戴尔豪斯大学数学建模课程的代写成功案例。

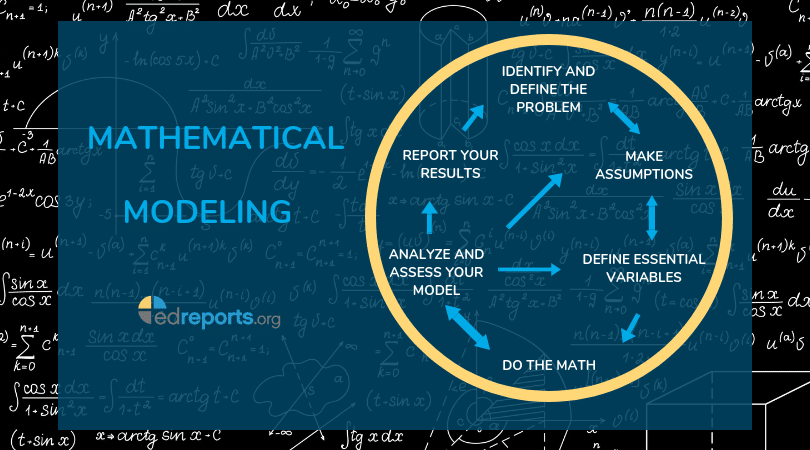
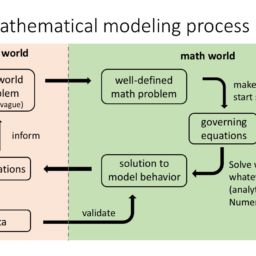
MATH2300课程简介
(3) Credit Hours
Lab-based activities designed to strengthen and expand knowledge of topics in secondary mathematics, focusing on topics from precalculus and elementary calculus. Explorations will involve the use of multiple representations, transformations, data analysis techniques and interconnections among geometry, probability and algebra. Most labs will include significant use of various technologies. The use of quantitative approaches and building relationships between discrete and continuous reasoning will be recurrent themes. Every semester. Prerequisites: Admissions to the UTeaChattanooga program; university, UTSM, and major department grade point averages of at least 2.5; UTSM 1020 and MATH 1920, MATH 1921 and MATH 2200 with minimum grades of C or UTeaChattanooga Co-Director approval.
Prerequisites
Course outline: Dynamical systems, basic probability, queing theory, selected topics.
References: The textbook for this course is “A Course in Mathematical Modeling” by Mooney and Swift. Some of the material will be outside the textbook in which case appropriate references will be provided.
Advising and Access Services Center: Students may request accommodation as a result of barriers related to disability, religious obligation, or any characteristic under the Nova Scotia Human Rights Act. Students who require academic accommodation for either classroom participation or the writing of tests and exams should make their request to the Advising and Access Services Center (AASC) prior to or at the outset of the regular academic year. Please visit www.dal.ca/access for more information and to obtain the Request for Accommodation – Form A.
MATH2300 Mathematical Modeling HELP(EXAM HELP, ONLINE TUTOR)
a. Consider the DE $\frac{d y}{d t}+\frac{a}{t} y=t^{a-1}$, where $a$ is a constant.
i. Find the general solution $y_1(t)$ of the given DE for $a=2$.
ii. Find the general solution $y_2(t)$ of the given DE for $a=-2$.
b. Describe the behaviour of each of these solutions as $t \rightarrow \infty$.
c. Find an initial condition $y_2(1)=y_0$ for $y_2(t)$ such that, as $t \rightarrow \infty, y_1(t) \rightarrow y_2(t)$.
d. It appears that for $a \neq 0$, the solutions of the given DE consist of power functions $t^a$ and $t^{-a}$. Determine whether this is also true if $a=0$
a. Explain how you know that there exists a unique solution of the IVP $\frac{d y}{d t}=2 t y^2$, $y\left(t_0\right)=y_0$ for every point $\left(t_0, y_0\right)$ in the plane.
b. Solve the IVP $\frac{d y}{d t}=2 t y^2, y(0)=y_0$, and state any equilibrium solutions.
c. Show that, for the solutions in part b.,
i. every solution is symmetric about the $y$-axis;
ii. if $y_0>0$, the solution has a finite domain bounded by two vertical asymptotes:
iii. if $y_0<0$, the solution is a negative function defined for all real $t$, and is asymptotic to an equilibrium solution as $|t| \rightarrow \infty$.
d. Illustrate how the solutions depend on the initial condition $y_0$ by sketching the solutions for $y_0=-2,-1,0, \frac{1}{4}, 1$.
For each of the given DEs, state whether the DE is linear, separable, exact, homogeneous, or a Bernoulli equation, or reducible to a linear or separable DE. Where appropriate, state the substitution required to reduce or solve the DE. Where a DE is of more than one type, state all possibilities. DO NOT SOLVE.
a. $\sqrt{\frac{y}{x}}+\cos x+\sqrt{\frac{x}{y}} \frac{d y}{d x}=0$
d. $\frac{d y}{d x}=\frac{y}{x+\sqrt{x^2+y^2}}$
b. $\frac{d y}{d t}+t y=y$
e. $y^{\prime \prime}+4 y^{\prime}=t^2$
c. $\frac{d y}{d t}=\frac{t y^2-\sin t \cos t}{\left(1-t^2\right) y}$
a. Find the integral curves of the exact DE $2 x-y+(2 y-x) \frac{d y}{d x}=0$. (Easy.)
b. Show that the integral curve through $(1,1)$ defines exactly two explicit functions $y_1(x)$ and $y_2(x)$, and state the interval on which these functions are defined.
c. For the IVP $\frac{d y}{d x}=\frac{y-2 x}{2 y-x}, y(1)=1$, the Existence-Uniqueness Theorem predicts possible trouble where $y=\frac{x}{2}$. Since $y_1(x)$ passes through $(1,1)$, it contains the solution of this IVP. What portion of $y_1(x)$ is this solution?
d. The integral curve in b. is actually a ’tilted’ ellipse $\left(x-\frac{y}{2}\right)^2+\frac{3}{4} y^2=1$, with axes $y=x$ and $y=-x$. Sketch this ellipse, indicating the explicit solution through $(1,1)$. What is the slope of the ellipse as it crosses $y=\frac{x}{2}$ ?

MY-ASSIGNMENTEXPERT™可以为您提供MATHSTAT MATH2300 MATHEMATICAL MODELING数学建模的代写代考和辅导服务!