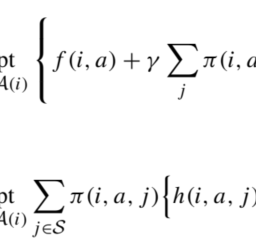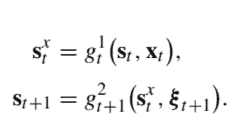如果你也在为遇到的matlab相关的难题发愁,请随时右上角联系我们的24/7代写客服。MATLAB®将为迭代分析和设计过程而调整的桌面环境与直接表达矩阵和阵列数学的编程语言相结合。它包括用于创建脚本的实时编辑器,这些脚本将代码、输出和格式化文本结合在可执行的笔记本中。
- 专业构建
MATLAB工具箱是专业开发的,经过严格的测试,并有完整的文件记录。 - 拥有互动式应用程序
MATLAB应用程序让您看到不同的算法是如何与您的数据一起工作的。迭代直到您得到您想要的结果,然后自动生成一个MATLAB程序来重现或自动完成您的工作。 - 以及扩展的能力
只需稍加修改代码,就可以将您的分析扩展到集群、GPU和云上运行。不需要重写你的代码或学习大数据编程和内存外技术。
my-assignmentexpert™ matlab作业代写,免费提交作业要求, 满意后付款,成绩80\%以下全额退款,安全省心无顾虑。专业硕 博写手团队,所有订单可靠准时,保证 100% 原创。my-assignmentexpert™, 最高质量的matlab作业代写作业代写,服务覆盖北美、欧洲、澳洲等 国家。 在代写价格方面,考虑到同学们的经济条件,在保障代写质量的前提下,我们为客户提供最合理的价格。 由于统计Statistics作业种类很多,同时其中的大部分作业在字数上都没有具体要求,因此matlab作业代写作业代写的价格不固定。通常在matlab专家查看完作业要求之后会给出报价。作业难度和截止日期对价格也有很大的影响。
想知道您作业确定的价格吗? 免费下单以相关学科的专家能了解具体的要求之后在1-3个小时就提出价格。专家的 报价比上列的价格能便宜好几倍。
my-assignmentexpert™ 为您的留学生涯保驾护航 在matlab作业代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的应用数学applied math代写服务。我们的专家在matlab作业代写方面经验极为丰富,各种matlab作业代写相关的作业也就用不着 说。
我们提供的matlab作业代写及其相关学科的代写,服务范围广, 其中包括但不限于:
- 数据分析
- 数值与符号计算
- 工程与科学绘图
- 控制系统设计
- 航天工业
- 汽车工业
- 生物医学工程
- 语音处理

运筹学代写
数学代写|matlab作业代写|Discrete Resource Allocation: The Knapsack Problem
The knapsack problem, in its literal version, concerns the selection of a subset of items, to be placed into a finite capacity knapsack. Each item features a weight, or a volume, and a value, and we want to find a subset of items with maximum value, subject to the knapsack capacity constraint. We assume a one-dimensional capacity, which may be expressed either in terms of maximum allowed weight or maximum allowed volume. A more interesting interpretation concerns the allocation of a limited budget $B$ to a set of $n$ investments with resource requirement $w_{k}$ and monetary payoff $v_{k}, k=1, \ldots, n$. If we introduce binary decision variables to model the selection of each item,
$$
x_{k}= \begin{cases}1 & \text { if item } k \text { is selected } \ 0 & \text { otherwise }\end{cases}
$$
the problem can be easily formulated as a pure binary linear program:
$$
\begin{aligned}
\max & \sum_{k=1}^{n} v_{k} x_{k} \
\text { s.t. } & \sum_{k=1}^{n} w_{k} x_{k} \leq B \
& x_{k} \in{0,1} \quad \forall k
\end{aligned}
$$
Note that we are assuming a discrete budget allocation, as the selection of an activity is an all-or-nothing decision. ${ }^{1}$ The problem can be solved quite efficiently
by state-of-the-art branch-and-cut algorithms for integer linear programming, but let us pursue a DP approach.
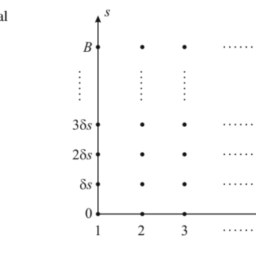
The problem is not dynamic in itself, but we may recast it as a sequential resource allocation problem. We introduce a fictitious discrete time index $k$, corresponding to items. For each time index (or decision stage) $k=1, \ldots, n$, we have to decide whether to include item $k$ in the subset or not. At stage $k=1$, we have the full budget $B$ at our disposal and we have to decide whether to include item 1 or not in the subset. This is a difficult task, as we must assess the tradeoff between consuming $w_{1}$ units of budget and earning a reward $v_{1}$, while wondering about the whole remaining set ${2, \ldots, n}$ of items. At stage $k=n$, however, the problem is trivial, since we have only to consider the set ${n}$ consisting of the last item, given the residual budget. If the last item fits the residual budget, just include it in the selection; otherwise, forget about it. Indeed, the natural state variable at stage $k$ is the available budget $s_{k}$ before selecting item $k$, and the decision variable at each stage is the binary variable $x_{k}$ that we have introduced above. In this case, since there is no item $k=0$, we sway a bit from the usual notation, and write the state transition equation as
$$
s_{k+1}=s_{k}-w_{k} x_{k}, \quad k=1, \ldots, n
$$
with initial condition $s_{1}=B$. Hence, we may define the following value function:
$V_{k}(s) \doteq$ profit from the optimal subset selection within the set of items ${k, k+1, \ldots, n}$, when the residual budget is $s$.
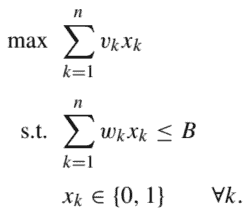
matlab代写
数学代写|MATLAB作业代写|DISCRETE RESOURCE ALLOCATION: THE KNAPSACK PROBLEM
背包问题,就其字面意义而言,涉及选择一个项目子集,将其放入有限容量的背包中。每个物品都有一个重量或体积和一个价值,我们希望找到一个具有最大值的物品子集,受背包容量限制。我们假设一维容量,可以用最大允许重量或最大允许体积表示。一个更有趣的解释涉及有限预算的分配乙对一组n有资源需求的投资在到和金钱回报v到,到=1,…,n. 如果我们引入二元决策变量来模拟每个项目的选择,
X到={1 如果项目 到 被选中 0 否则
该问题可以很容易地表述为纯二元线性规划:
最大限度∑到=1nv到X到 英石 ∑到=1n在到X到≤乙 X到∈0,1∀到
请注意,我们假设一个离散的预算分配,因为选择一项活动是一个全有或全无的决定。1问题可以非常有效地解决
通过用于整数线性规划的最先进的分支和切割算法,但让我们追求一种 DP 方法。
该问题本身不是动态的,但我们可以将其重新定义为顺序资源分配问题。我们引入一个虚构的离散时间索引到,对应项目。对于每个时间索引○rd和C一世s一世○ns吨一种G和 到=1,…,n,我们必须决定是否包含项目到在子集中与否。在阶段到=1, 我们有完整的预算乙由我们支配,我们必须决定是否在子集中包含第 1 项。这是一项艰巨的任务,因为我们必须评估消费之间的权衡在1预算单位和获得奖励v1,同时想知道剩下的整个集合2,…,n的项目。在阶段到=n,然而,这个问题是微不足道的,因为我们只需要考虑集合n由最后一项组成,给定剩余预算。如果最后一项符合剩余预算,只需将其包括在选择中;否则,忘记它。确实,阶段的自然状态变量到是可用预算s到在选择项目之前到,每个阶段的决策变量是二元变量X到我们在上面介绍过。在这种情况下,由于没有项目到=0,我们稍微偏离通常的符号,并将状态转移方程写为
s到+1=s到−在到X到,到=1,…,n
有初始条件s1=乙. 因此,我们可以定义以下价值函数:
五到(s)≐从项目集中的最优子集选择中获利到,到+1,…,n, 当剩余预算为s.

统计代考
统计是汉语中的“统计”原有合计或汇总计算的意思。 英语中的“统计”(Statistics)一词来源于拉丁语status,是指各种现象的状态或状况。
数论代考
数论(number theory ),是纯粹数学的分支之一,主要研究整数的性质。 整数可以是方程式的解(丢番图方程)。 有些解析函数(像黎曼ζ函数)中包括了一些整数、质数的性质,透过这些函数也可以了解一些数论的问题。 透过数论也可以建立实数和有理数之间的关系,并且用有理数来逼近实数(丢番图逼近)
数值分析代考
数值分析NumericalAnalysis,又名“计算方法”,是研究分析用计算机求解数学计算问题的数值计算方法及其理论的学科。 它以数字计算机求解数学问题的理论和方法为研究对象,为计算数学的主体部分。
随机过程代写
随机过程,是依赖于参数的一组随机变量的全体,参数通常是时间。 随机变量是随机现象的数量表现,其取值随着偶然因素的影响而改变。 例如,某商店在从时间t0到时间tK这段时间内接待顾客的人数,就是依赖于时间t的一组随机变量,即随机过程
MATLAB代写
MATLAB 是一种用于技术计算的高性能语言。它将计算、可视化和编程集成在一个易于使用的环境中,其中问题和解决方案以熟悉的数学符号表示。典型用途包括:数学和计算算法开发建模、仿真和原型制作数据分析、探索和可视化科学和工程图形应用程序开发,包括图形用户界面构建MATLAB 是一个交互式系统,其基本数据元素是一个不需要维度的数组。这使您可以解决许多技术计算问题,尤其是那些具有矩阵和向量公式的问题,而只需用 C 或 Fortran 等标量非交互式语言编写程序所需的时间的一小部分。MATLAB 名称代表矩阵实验室。MATLAB 最初的编写目的是提供对由 LINPACK 和 EISPACK 项目开发的矩阵软件的轻松访问,这两个项目共同代表了矩阵计算软件的最新技术。MATLAB 经过多年的发展,得到了许多用户的投入。在大学环境中,它是数学、工程和科学入门和高级课程的标准教学工具。在工业领域,MATLAB 是高效研究、开发和分析的首选工具。MATLAB 具有一系列称为工具箱的特定于应用程序的解决方案。对于大多数 MATLAB 用户来说非常重要,工具箱允许您学习和应用专业技术。工具箱是 MATLAB 函数(M 文件)的综合集合,可扩展 MATLAB 环境以解决特定类别的问题。可用工具箱的领域包括信号处理、控制系统、神经网络、模糊逻辑、小波、仿真等。