如果你也在 怎样代写matlab这个学科遇到相关的难题,请随时右上角联系我们的24/7代写客服。matlab是由MathWorks公司开发的一种专有的多范式编程语言和数字计算环境。MATLAB允许进行矩阵操作、绘制函数和数据、实现算法、创建用户界面以及与用其他语言编写的程序对接。
matlab尽管MATLAB主要用于数值计算,但一个可选的工具箱使用MuPAD符号引擎,允许访问符号计算能力。一个额外的软件包,Simulink,为动态和嵌入式系统增加了图形化的多域仿真和基于模型的设计。截至2020年,MATLAB在全球拥有超过400万用户。他们来自工程、科学和经济的各种背景。
my-assignmentexpert™ matlab作业代写,免费提交作业要求, 满意后付款,成绩80\%以下全额退款,安全省心无顾虑。专业硕 博写手团队,所有订单可靠准时,保证 100% 原创。my-assignmentexpert™, 最高质量的matlab作业代写,服务覆盖北美、欧洲、澳洲等 国家。 在代写价格方面,考虑到同学们的经济条件,在保障代写质量的前提下,我们为客户提供最合理的价格。 由于统计Statistics作业种类很多,同时其中的大部分作业在字数上都没有具体要求,因此matlab作业代写的价格不固定。通常在经济学专家查看完作业要求之后会给出报价。作业难度和截止日期对价格也有很大的影响。
想知道您作业确定的价格吗? 免费下单以相关学科的专家能了解具体的要求之后在1-3个小时就提出价格。专家的 报价比上列的价格能便宜好几倍。
my-assignmentexpert™ 为您的留学生涯保驾护航 在数学Mathematics作业代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的matlab代写服务。我们的专家在数学Mathematics代写方面经验极为丰富,各种matlab相关的作业也就用不着 说。
我们提供的matlab及其相关学科的代写,服务范围广, 其中包括但不限于:
数学代写|matlab代写|Introduction
Optimization is the term often used for minimizing or maximizing a function. It is sufficient to consider the problem of minimization only; maximization of $F(\mathbf{x})$ is achieved by simply minimizing $-F(\mathbf{x})$. In engineering, optimization is closely related to design. The function $F(\mathbf{x})$, called the merit function or objective function, is the quantity that we wish to keep as small as possible, such as cost or weight. The components of $\mathbf{x}$, known as the design variables, are the quantities that we are free to adjust. Physical dimensions (lengths, areas, angles, etc.) are common examples of design variables.
Optimization is a large topic with many books dedicated to it. The best we can do in limited space is to introduce a few basic methods that are good enough for problems that are reasonably well behaved and don’t involve too many design variables. By omitting the more sophisticated methods, we may actually not miss all that much. All optimization algorithms are unreliable to a degree-any one of them may work on one problem and fail on another. As a rule of thumb, by going up in sophistication we gain computational efficiency, but not necessarily reliability.
The algorithms for minimization are iterative procedures that require starting values of the design variables $\mathbf{x}$. If $F(\mathbf{x})$ has several local minima, the initial choice of $x$ determines which of these will be computed. There is no guaranteed way of finding the global optimal point. One suggested procedure is to make several computer runs using different starting points and pick the best result.
More often than not, the design is also subjected to restrictions, or constraints, which may have the form of equalities or inequalities. As an example, take the minimum weight design of a roof truss that has to carry a certain loading. Assume that the layout of the members is given, so that the design variables are the cross-sectional areas of the members. Here the design is dominated by inequality constraints that consist of prescribed upper limits on the stresses and possibly the displacements.
数学代写|matlab代写|Minimization Along a Line
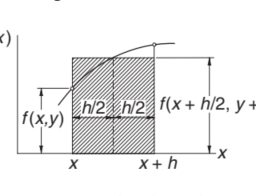
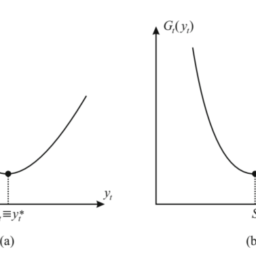
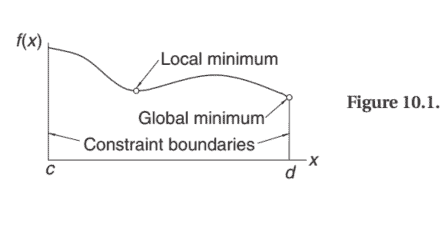
Consider the problem of minimizing a function $f(x)$ of a single variable $x$ with the constraints $c \leq x \leq d$. A hypothetical plot of the function is shown in Fig. 10.1. There are two minimum points: a stationary point characterized by $f^{\prime}(x)=0$ that represents a local minimum, and a global minimum at the constraint boundary. It appears that finding the global minimum is simple. All the stationary points could be located by finding the roots of $d f / d x=0$, and each constraint boundary may be checked for a global minimum by evaluating $f(c)$ and $f(d)$. Then why do we need an optimization algorithm? We need it if $f(\mathbf{x})$ is difficult or impossible to differentiate; for example, if $f$ represents a complex computer algorithm.
数学代写|MATLAB代写|Conjugate Gradient Methods
We now look at optimization in $n$-dimensional design space. The objective is to minimize $F(\mathbf{x})$, where the components of $\mathbf{x}$ are the $n$ independent design variables. One way to tackle the problem is to use a succession of one-dimensional minimizations to close in on the optimal point. The basic strategy is
- Choose a point $\mathrm{x}_{0}$ in the design space.
- loop with $i=1,2,3, \ldots$
Choose a vector $\mathbf{v}{i}$. Minimize $F(\mathbf{x})$ along the line through $\mathbf{x}{i-1}$ in the direction of $\mathbf{v}{i}$. Let the minimum point be $\mathbf{x}{i}$.
if $\left|\mathbf{x}{i}-\mathbf{x}{i-1}\right|<\varepsilon$ exit loop - end loop
The minimization along a line can be accomplished with any one-dimensional optimization algorithm (such as the golden section search). The only question left open is how to choose the vectors $\mathbf{v}_{i}$.
matlab代写
数学代写|MATLAB代写|INTRODUCTION
优化是经常用于最小化或最大化函数的术语。只考虑最小化问题就足够了;最大化F(X)通过简单地最小化来实现−F(X). 在工程中,优化与设计密切相关。功能F(X),称为评价函数或目标函数,是我们希望保持尽可能小的量,例如成本或重量。的组成部分X,称为设计变量,是我们可以自由调整的数量。物理尺寸l和nG吨Hs,一种r和一种s,一种nGl和s,和吨C.是设计变量的常见示例。
优化是一个很大的话题,有很多书专门讨论它。在有限的篇幅内,我们能做的最好的事情就是介绍一些基本的方法,这些方法足以解决那些表现得相当好的问题并且不涉及太多设计变量的问题。通过省略更复杂的方法,我们实际上可能不会错过那么多。所有的优化算法在一定程度上都是不可靠的——它们中的任何一个都可能在一个问题上工作而在另一个问题上失败。根据经验,通过提高复杂性,我们可以获得计算效率,但不一定是可靠性。
最小化算法是迭代过程,需要设计变量的起始值X. 如果F(X)有几个局部最小值,初始选择X确定将计算其中的哪些。没有保证找到全局最优点的方法。一种建议的程序是使用不同的起点让多台计算机运行并选择最佳结果。
通常情况下,设计也受到限制或约束,可能具有等式或不等式的形式。例如,以必须承载一定载荷的屋架的最小重量设计为例。假设给定构件的布局,则设计变量为构件的横截面积。这里的设计受不等式约束的支配,这些不等式约束由规定的应力上限和可能的位移组成。
数学代写|MATLAB代写|MINIMIZATION ALONG A LINE
考虑最小化函数的问题F(X)单一变量的X有约束C≤X≤d. 该函数的假设图如图 10.1 所示。有两个最小点:一个固定点,其特征为F′(X)=0表示局部最小值和约束边界处的全局最小值。似乎找到全局最小值很简单。所有的静止点都可以通过找到dF/dX=0,并且每个约束边界可以通过评估来检查全局最小值F(C)和F(d). 那为什么我们需要优化算法呢?如果我们需要它F(X)难以或不可能区分;例如,如果F表示复杂的计算机算法。
数学代写|MATLAB代写|CONJUGATE GRADIENT METHODS
我们现在看一下优化n维设计空间。目标是最小化F(X),其中的组件X是n独立的设计变量。解决该问题的一种方法是使用一系列一维最小化来逼近最优点。基本策略是
- 选择一个点X0在设计空间。
- 循环一世=1,2,3,…
选择一个向量$\mathbf{v}{i}$. Minimize $F(\mathbf{x})$ along the line through $\mathbf{x}{i-1}$ in the direction of $\mathbf{v}{i}$. Let the minimum point be $\mathbf{x}{i}$. - if $\left|\mathbf{x}{i}-\mathbf{x}{i-1}\right|<\varepsilon$ 退出循环
- end loop
沿线的最小化可以用任何一维优化算法来完成s在CH一种s吨H和G这ld和ns和C吨一世这ns和一种rCH. 唯一悬而未决的问题是如何选择向量在一世.

数学代写|matlab代写 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。