如果你也在 怎样代写统计力学statistical mechanics这个学科遇到相关的难题,请随时右上角联系我们的24/7代写客服。统计力学statistical mechanics在物理学中,是一个数学框架,它将统计方法和概率理论应用于大型微观实体的集合。它不假设或假定任何自然法则,而是从这些集合体的行为来解释自然界的宏观行为。
统计力学statistical mechanics产生于经典热力学的发展,对该领域而言,它成功地解释了宏观物理特性–如温度、压力和热容量–以围绕平均值波动的微观参数和概率分布为特征。这建立了统计热力学和统计物理学的领域。
my-assignmentexpert™ 统计力学statistical mechanics作业代写,免费提交作业要求, 满意后付款,成绩80\%以下全额退款,安全省心无顾虑。专业硕 博写手团队,所有订单可靠准时,保证 100% 原创。my-assignmentexpert™, 最高质量的统计力学statistical mechanics作业代写,服务覆盖北美、欧洲、澳洲等 国家。 在代写价格方面,考虑到同学们的经济条件,在保障代写质量的前提下,我们为客户提供最合理的价格。 由于统计Statistics作业种类很多,同时其中的大部分作业在字数上都没有具体要求,因此统计力学statistical mechanics作业代写的价格不固定。通常在经济学专家查看完作业要求之后会给出报价。作业难度和截止日期对价格也有很大的影响。
想知道您作业确定的价格吗? 免费下单以相关学科的专家能了解具体的要求之后在1-3个小时就提出价格。专家的 报价比上列的价格能便宜好几倍。
my-assignmentexpert™ 为您的留学生涯保驾护航 在物理physics作业代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的物理physics代写服务。我们的专家在统计力学statistical mechanics代写方面经验极为丰富,各种统计力学statistical mechanics相关的作业也就用不着 说。
我们提供的统计力学statistical mechanics及其相关学科的代写,服务范围广, 其中包括但不限于:
- 化学统计力学 chemistry,statistical mechanics
- 非平衡统计力学 Nonequilibrium Statistical Mechanics
- 玻耳兹曼分布律 Boltzmann distribution law
物理代写|统计力学代写Statistical mechanics代考|Microstates and Macrostates
We will start by defining macroscopic laws more generally and explain what “derive” means.
The microstates of a classical mechanical system are elements of $\mathbb{R}^{6 N}$, and we wrote in Sect. $3.3$ a vector $\mathbf{x} \in \mathbb{R}^{\mathbf{6 N}}$ as a pair $\mathbf{x}=(\mathbf{q}, \mathbf{p})$, with $\mathbf{q}=\left(\vec{q}{1}, \vec{q}{2}, \ldots, \vec{q}{N}\right) \in$ $\mathbb{R}^{3 N}, \mathbf{p}=\left(\vec{p}{1}, \vec{p}{2}, \ldots, \vec{p}{N}\right) \in \mathbb{R}^{3 N}$ and defined the time evolution of $\mathbf{x}(t)=T^{t}(\mathbf{x}(0)$ through Hamilton’s equations (3.3.3), (3.3.4), (3.3.10).
If one works with closed systems, as one usually does, one considers a closed and bounded subset $\Omega \subset \mathbb{R}^{6 N}$ (the spatial part is bounded because the system is enclosed in a box and its velocities are bounded because the total energy of the system is finite $^{1}$ ) which we will refer to as the phase space of the system.
Our definition of the macrostate will be more vague: we are all familiar with macroscopic quantities like the volume, the pressure, the temperature or the density of physical systems. These are quantities that we have a direct access to, without knowing anything about the microscopic composition of matter. In fact, physicists started by studying such quantities long before the had any idea about atoms and people like the 19th century Austrian physicist Ernst Mach studied them while denying the existence of atoms.
As long as we study terrestrial phenomena, those macroscopic quantities characterize systems composed of a number of atoms which is very large but too large. The objects studied here are, to use Lars Onsager phrase “large compared to atoms, but small compared to the sun”, which means in practice that we can neglect gravitational forces.
To define abstractly a macrostate, we introduce a map from the phase space of the system into $\mathbb{R}^{L}$ :
$$
M: \Omega \rightarrow \mathbb{R}^{L}
$$
where $L<<N$. Those variables could be the energy or the density but we will give more examples of such variables in a moment. By definition, $M(\mathbf{x})$ is the macrostate associated to the microstate $\mathbf{x}$. The important point is that the macrostate is a function of the microstate. For example, if we know $\mathbf{x}=(\mathbf{q}, \mathbf{p})$, then we know the total energy of the system given by (3.3.11). Obviously, we also know the total density of the system. The condition $L<<N$ means that we have far fewer macroscopic variables than microscopic ones; otherwise there would be no point in speaking of a macroscopic description.
物理代写|统计力学代写Statistical mechanics代考|Dominance of the Equilibrium Macrostate
The most important property of our map $M$, which will allow us to understand the notion of equilibrium is that this map is many to one in a way that depends on value taken by $M$.
To explain this, think again of the simple example of $N$ coin tossing: a microstate is a sequence of results e.g. $(H, T, H, H, \ldots, T)$ and $\Omega$ is the set of such sequences; we have $|\Omega|=2^{N}$.
The macrostate is $M=\left(N_{0}, N_{1}\right)$, with $N_{0}=$ number of heads, $N_{1}=$ number of tails.
If $N_{0}=N$, it corresponds to a unique microstate $(H, H, H, H, \ldots, H)$
But if $N_{0}=\frac{N}{2}$ then there are approximately $\frac{2^{N}}{\sqrt{N}}$ microstates giving rise to that value of $M$ (see (6.2.7) below).
In (2.3.4), we gave the number $\left|M^{-1}\left(N_{0}\right)\right|$ of microstates corresponding to a given value of $M$, i.e. of $N_{0}$ :
$$
\left|M^{-1}\left(N_{0}\right)\right|=\frac{N !}{N_{0} ! N_{1} !}=\frac{N !}{N_{0} !\left(N-N_{0}\right) !}
$$
物理代写|统计力学代写STATISTICAL MECHANICS代考|Typicality
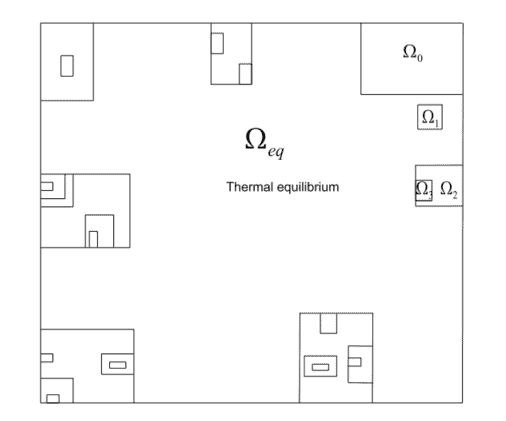
In each of the examples above, the configurations in $\Omega_{e q}$ are typical, to use the term defined Sect. 2.3.1. In the situations considered in statistical mechanics, we always have a large parameter $N$, which, for mathematical convenience, we let tend to $\infty$. The typicality of the configurations in $\Omega_{e q}$ is expressed by bounds of the form (6.2.6, 6.2.11).
As we discussed in Sect. $2.6$ typical events do not need to be explained, since, by definition of “probable” or by Cournot’s principle, typical events are what we expect to happen. Thus, equilibrium states do not need to be explained. What need to be explained are non-equilibrium states and the evolution from non-equilibrium states towards equilibrium ones .
统计力学代写
物理代写|统计力学代写STATISTICAL MECHANICS代考|MICROSTATES AND MACROSTATES
我们将从更一般地定义宏观规律开始,并解释“推导”的含义。
经典机械系统的微观状态是R6ñ,我们在 Sect.3.3一个向量X∈R6ñ作为一对X=(q,p), 其中 $\mathbf{q}=\left(\vec{q} {1}, \vec{q} {2}, \ldots, \vec{q} {N}\right) \in\mathbb{R}^{3 N}, \mathbf{p}=\left(\vec{p} {1}, \vec{p} {2}, \ldots, \vec{p} {N}\对)\in \mathbb{R}^{3 N}一种ndd和F一世n和d吨H和吨一世米和和在这l在吨一世这n这F\mathbf{x}吨=T^{t}X(0$ 通过汉密尔顿方程3.3.3, 3.3.4,3.3.10.
如果像通常那样使用封闭系统,则考虑一个封闭且有界的子集Ω⊂R6ñ 吨H和sp一种吨一世一种lp一种r吨一世sb这在nd和db和C一种在s和吨H和s是s吨和米一世s和nCl这s和d一世n一种b这X一种nd一世吨s在和l这C一世吨一世和s一种r和b这在nd和db和C一种在s和吨H和吨这吨一种l和n和rG是这F吨H和s是s吨和米一世sF一世n一世吨和$1$我们将其称为系统的相空间。
我们对宏观状态的定义会更加模糊:我们都熟悉物理系统的体积、压力、温度或密度等宏观量。这些是我们可以直接获得的量,而不知道物质的微观组成。事实上,早在 19 世纪奥地利物理学家恩斯特·马赫(Ernst Mach)等人对原子和人有任何了解之前,物理学家就开始研究这些量,同时否认原子的存在。
只要我们研究地球现象,那些宏观量就表征了由许多原子组成的系统,这些原子非常大但太大了。这里研究的物体,用 Lars Onsager 的话来说是“比原子大,比太阳小”,这意味着在实践中我们可以忽略引力。
为了抽象地定义一个宏观状态,我们将系统相空间的映射引入到R大号 :
米:Ω→R大号
在哪里大号<<ñ. 这些变量可能是能量或密度,但稍后我们将给出更多此类变量的示例。根据定义,米(X)是与微观状态相关的宏观状态X. 重要的一点是宏观状态是微观状态的函数。例如,如果我们知道X=(q,p),那么我们知道系统的总能量由下式给出3.3.11. 显然,我们也知道系统的总密度。条件大号<<ñ意味着我们的宏观变量比微观变量少得多;否则,谈宏观描述就没有意义了。
物理代写|统计力学代写STATISTICAL MECHANICS代考|DOMINANCE OF THE EQUILIBRIUM MACROSTATE
我们地图最重要的属性米,这将使我们理解均衡的概念是,这张地图是多对一的,其方式取决于米.
为了解释这一点,再想想简单的例子ñ抛硬币:微观状态是一系列结果,例如(H,吨,H,H,…,吨)和Ω是这样的序列的集合;我们有|Ω|=2ñ.
宏观状态是米=(ñ0,ñ1), 和ñ0=头数,ñ1=尾数。
如果ñ0=ñ,它对应于一个独特的微观状态(H,H,H,H,…,H)
但如果ñ0=ñ2那么大约有2ññ产生该值的微观状态米 s和和(6.2.7以下)。
在2.3.4,我们给出了数字|米−1(ñ0)|对应于给定值的微观状态米,即ñ0 :
|米−1(ñ0)|=ñ!ñ0!ñ1!=ñ!ñ0!(ñ−ñ0)!
物理代写|统计力学代写STATISTICAL MECHANICS代考|TYPICALITY
在上面的每个示例中,配置Ω和q是典型的,使用术语定义的教派。2.3.1。在统计力学考虑的情况下,我们总是有一个很大的参数ñ, 其中,为了数学上的方便,我们让倾向于∞. 配置的典型性Ω和q由形式的边界表示6.2.6,6.2.11.
正如我们在 Sect 中讨论的那样。2.6典型事件不需要解释,因为根据“可能”的定义或古诺原则,典型事件就是我们期望发生的事情。因此,不需要解释平衡状态。需要解释的是非平衡态和非平衡态向平衡态的演化。

物理代写|统计力学作业代写statistical mechanics代考 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。
电磁学代考
物理代考服务:
物理Physics考试代考、留学生物理online exam代考、电磁学代考、热力学代考、相对论代考、电动力学代考、电磁学代考、分析力学代考、澳洲物理代考、北美物理考试代考、美国留学生物理final exam代考、加拿大物理midterm代考、澳洲物理online exam代考、英国物理online quiz代考等。
光学代考
光学(Optics),是物理学的分支,主要是研究光的现象、性质与应用,包括光与物质之间的相互作用、光学仪器的制作。光学通常研究红外线、紫外线及可见光的物理行为。因为光是电磁波,其它形式的电磁辐射,例如X射线、微波、电磁辐射及无线电波等等也具有类似光的特性。
大多数常见的光学现象都可以用经典电动力学理论来说明。但是,通常这全套理论很难实际应用,必需先假定简单模型。几何光学的模型最为容易使用。
相对论代考
上至高压线,下至发电机,只要用到电的地方就有相对论效应存在!相对论是关于时空和引力的理论,主要由爱因斯坦创立,相对论的提出给物理学带来了革命性的变化,被誉为现代物理性最伟大的基础理论。
流体力学代考
流体力学是力学的一个分支。 主要研究在各种力的作用下流体本身的状态,以及流体和固体壁面、流体和流体之间、流体与其他运动形态之间的相互作用的力学分支。
随机过程代写
随机过程,是依赖于参数的一组随机变量的全体,参数通常是时间。 随机变量是随机现象的数量表现,其取值随着偶然因素的影响而改变。 例如,某商店在从时间t0到时间tK这段时间内接待顾客的人数,就是依赖于时间t的一组随机变量,即随机过程
Matlab代写
MATLAB 是一种用于技术计算的高性能语言。它将计算、可视化和编程集成在一个易于使用的环境中,其中问题和解决方案以熟悉的数学符号表示。典型用途包括:数学和计算算法开发建模、仿真和原型制作数据分析、探索和可视化科学和工程图形应用程序开发,包括图形用户界面构建MATLAB 是一个交互式系统,其基本数据元素是一个不需要维度的数组。这使您可以解决许多技术计算问题,尤其是那些具有矩阵和向量公式的问题,而只需用 C 或 Fortran 等标量非交互式语言编写程序所需的时间的一小部分。MATLAB 名称代表矩阵实验室。MATLAB 最初的编写目的是提供对由 LINPACK 和 EISPACK 项目开发的矩阵软件的轻松访问,这两个项目共同代表了矩阵计算软件的最新技术。MATLAB 经过多年的发展,得到了许多用户的投入。在大学环境中,它是数学、工程和科学入门和高级课程的标准教学工具。在工业领域,MATLAB 是高效研究、开发和分析的首选工具。MATLAB 具有一系列称为工具箱的特定于应用程序的解决方案。对于大多数 MATLAB 用户来说非常重要,工具箱允许您学习和应用专业技术。工具箱是 MATLAB 函数(M 文件)的综合集合,可扩展 MATLAB 环境以解决特定类别的问题。可用工具箱的领域包括信号处理、控制系统、神经网络、模糊逻辑、小波、仿真等。