微积分note Functions and Sequences General Considerations

As discussed earlier, the concept of a function is that of something which gives a unique output for a given input.

Definition 4.1.1 Consider two sets, $D$ and $R$ along with a rule which assigns a unique element of $R$ to every element of $D$. This rule is called a function and it is denoted by a letter such as $f$. The symbol, $D(f)=D$ is called the domain of $f$. The set $R$, also written $R(f)$, is called the range of $f$. The set of all elements of $R$ which are of the form $f(x)$ for some $x \in D$ is often denoted by $f(D)$. When $R=f(D)$, the function $f$ is said to be onto. It is common notation to write $f: D(f) \rightarrow R$ to denote the situation just described in this definition where $f$ is a function defined on $D$ having values in $R$.

Example 4.1.2 Consider the list of numbers, ${1,2,3,4,5,6,7} \equiv D$. Define a function which assigns an element of $D$ to $R \equiv{2,3,4,5,6,7,8}$ by $f(x) \equiv x+1$ for each $x \in D$.
In this example there was a clearly defined procedure which determined the function. However, sometimes there is no discernible procedure which yields a particular function.
Example 4.1.3 Consider the ordered pairs, $(1,2),(2,-2),(8,3),(7,6)$ and let $D \equiv$ ${1,2,8,7}$, the set of first entries in the given set of ordered pairs, $R \equiv{2,-2,3,6}$, the set of second entries, and let $f(1)=2, f(2)=-2, f(8)=3$, and $f(7)=6$.

Sometimes functions are not given in terms of a formula. For example, consider the following function defined on the positive real numbers having the following definition.
Example 4.1.4 For $x \in \mathbb{R}$ define
$$
f(x)=\left{\begin{array}{l}
\frac{1}{n} \text { if } x=\frac{m}{n} \text { in lowest terms for } m, n \in \mathbb{Z} \
0 \text { if } x \text { is not rational }
\end{array}\right.
$$
This is a very interesting function called the Dirichlet function. Note that it is not defined in a simple way from a formula.

Example $4.1 .5$ Let $D$ consist of the set of people who have lived on the earth except for Adam and for $d \in D$, let $f(d) \equiv$ the biological father of $d$. Then $f$ is a function.
This function is not the sort of thing studied in calculus but it is a function just the same. When $D(f)$ is not specified, it is understood to consist of everything for which $f$ makes sense. The following definition gives several ways to make new functions from old ones.

Definition 4.1.6 Let $f, g$ be functions with values in $\mathbb{F}$. Let a $b$ be points of F. Then af $+b g$ is the name of a function whose domain is $D(f) \cap D(g)$ which is defined as $(a f+b g)(x)=a f(x)+b g(x)$. The function $f g$ is the name of a function which is defined on $D(f) \cap D(g)$ given by $(f g)(x)=f(x) g(x)$. Similarly for $k$ an integer, $f^{k}$ is the name of a function defined as $f^{k}(x)=(f(x))^{k}$. The function $f / g$ is the name of a function whose domain is $D(f) \cap{x \in D(g): g(x) \neq 0}$ defined as $(f / g)(x)=f(x) / g(x)$. If $f: D(f) \rightarrow X$ and $g: D(g) \rightarrow Y$, then $g \circ f$ is the name of a function whose domain is ${x \in D(f): f(x) \in D(g)}$ which is defined as $g \circ f(x) \equiv g(f(x))$. This is called the composition of the two functions.

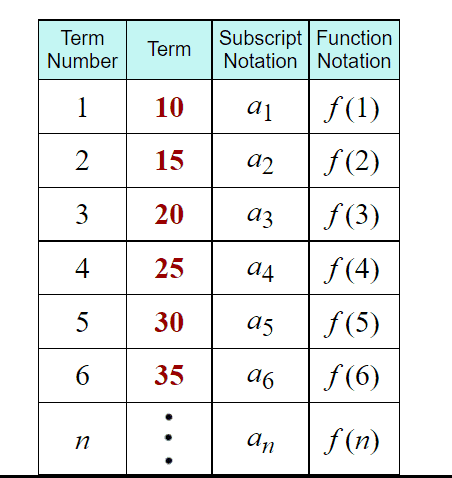
You should note that $f(x)$ is not a function. It is the value of the function at the point $x$. The name of the function is $f$. Nevertheless, people often write $f(x)$ to denote a function and it doesn’t cause too many problems in beginning courses. When this is done, the variable $x$ should be considered as a generic variable free to be anything in $D(f)$.

Sometimes people get hung up on formulas and think that the only functions of importance are those which are given by some simple formula. It is a mistake to think this way. Functions involve a domain and a range and a function is determined by what it does. This is an old idea. See Luke $6: 44$ where Jesus says essentially that you know a tree by its fruit. See also Matt. 7 about how to recognize false prophets. You look at what it does to determine what it is. As it is with false prophets and trees, so it is with functions. Although the idea is very old, its application to mathematics started with Dirichlet ${ }^{1}$ in the early 1800 ‘s because he was concerned with piecewise continuous functions which would be given by different descriptions on different intervals.

Example 4.1.7 Let $f(t)=t$ and $g(t)=1+t .$ Then $f g: \mathbb{R} \rightarrow \mathbb{R}$ is given by $f g(t)=$ $t(1+t)=t+t^{2} .$

Example 4.1.8 Let $f(t)=2 t+1$ and $g(t)=\sqrt{1+t}$. Then $g \circ f(t)=\sqrt{1+(2 t+1)}=$ $\sqrt{2 t+2}$ for $t \geq-1$. If $t<-1$ the inside of the square root sign is negative so makes no sense. Therefore, $g \circ f:{t \in \mathbb{R}: t \geq-1} \rightarrow \mathbb{R}$.

Note that in this last example, it was necessary to fuss about the domain of $g \circ f$ because $g$ is only defined for certain values of $t$.

The concept of a one to one function is very important. This is discussed in the following definition.

微积分note Functions and Sequences General Considerations

如前所述，函数的概念是为给定输入提供唯一输出的东西。

定义 4.1.1 考虑两个集合 $D$ 和 $R$ 以及将 $R$ 的唯一元素分配给 $D$ 的每个元素的规则。这条规则称为函数，它用一个字母表示，例如 $f$。符号$D(f)=D$ 称为$f$ 的域。集合$R$，也写作$R(f)$，称为$f$ 的范围。对于某个 $x \in D$，$R$ 的所有元素的集合，其形式为 $f(x)$，通常用 $f(D)$ 表示。当$R=f(D)$ 时，函数$f$ 被称为on on。通常的记法是写成 $f: D(f) \rightarrow R$ 来表示这个定义中刚刚描述的情况，其中 $f$ 是定义在 $D$ 上的函数，其值在 $R$ 中。

例 4.1.2 考虑数字列表 ${1,2,3,4,5,6,7} \equiv D$。定义一个函数，它通过 $f(x) \equiv x+1$ 为每个 $x 将 $D$ 的元素分配给 $R \equiv{2,3,4,5,6,7,8}$ \在 D$。
在这个例子中，有一个明确定义的过程来确定功能。然而，有时没有可识别的过程产生特定的功能。
示例 4.1.3 考虑有序对 $(1,2),(2,-2),(8,3),(7,6)$ 并让 $D \equiv$ ${1,2,8 ,7}$，给定有序对集合中的第一个条目的集合，$R \equiv{2,-2,3,6}$，第二个条目的集合，并且让 $f(1) =2，f(2)=-2，f(8)=3$，$f(7)=6$。

有时函数不是根据公式给出的。例如，考虑在具有以下定义的正实数上定义的以下函数。
例 4.1.4 对于 $x \in \mathbb{R}$ 定义
$$
f(x)=\left{\begin{数组}{l}
\frac{1}{n} \text { if } x=\frac{m}{n} \text { } m, n \in \mathbb{Z} \
0 \text { 如果 } x \text { 不是理性的 }
\end{数组}\对。
$$
这是一个非常有趣的函数，称为 Dirichlet 函数。请注意，它不是从公式中以简单的方式定义的。

示例 $4.1 .5$ 令 $D$ 由除了 Adam 和 $d \in D$ 之外都生活在地球上的人组成的集合，设 $f(d) \equiv$ 是 $d$ 的亲生父亲。那么 $f$ 是一个函数。
这个函数不是微积分中研究的那种东西，但它是一个相同的函数。当 $D(f)$ 未指定时，它被理解为由 $f$ 有意义的所有内容组成。以下定义提供了几种从旧函数创建新函数的方法。

定义 4.1.6 令 $f, g$ 是具有 $\mathbb{F}$ 值的函数。设 a $b$ 是 F 的点。那么 af $+bg$ 是定义域为 $D(f) \cap D(g)$ 的函数的名称，定义为 $(a f+bg)(x )=af(x)+bg(x)$。函数 $f g$ 是在 $(f g)(x)=f(x) g(x)$ 给出的 $D(f) \cap D(g)$ 上定义的函数的名称。类似地，对于整数 $k$，$f^{k}$ 是定义为 $f^{k}(x)=(f(x))^{k}$ 的函数的名称。函数 $f / g$ 是定义域为 $D(f) \cap{x \in D(g) 的函数的名称： g(x) \neq 0}$ 定义为 $(f / g )(x)=f(x)/g(x)$。如果 $f: D(f) \rightarrow X$ 和 $g: D(g) \rightarrow Y$，则 $g \circ f$ 是定义域为 ${x \in D(f ): f(x) \in D(g)}$ 定义为 $g \circ f(x) \equiv g(f(x))$。这称为两个函数的组合。

您应该注意 $f(x)$ 不是函数。它是函数在点 $x$ 处的值。函数的名称是 $f$。尽管如此，人们经常写 $f(x)$ 来表示一个函数，它不会在开始课程时造成太多问题。完成此操作后，变量 $x$ 应被视为一个通用变量，可以自由成为 $D(f)$ 中的任何内容。

有时人们会沉迷于公式，并认为唯一重要的函数是由一些简单公式给出的函数。以这种方式思考是错误的。函数涉及域和范围，函数由它的作用决定。这是一个古老的想法。参见路加福音 6 美元：44 美元，耶稣基本上说你从果子就知道一棵树。另见马特。 7关于如何识别假先知。你看看它做了什么来确定它是什么。就像假先知和树木一样，功能也是如此。虽然这个想法很古老，但它在数学上的应用始于 1800 年代早期的 Dirichlet ${ }^{1}$，因为他关心分段连续函数，这些函数将由不同间隔的不同描述给出。

例 4.1.7 令 $f(t)=t$ and $g(t)=1+t .$ 然后 $fg: \mathbb{R} \rightarrow \mathbb{R}$ 由 $fg(t) 给出=$ $t(1+t)=t+t^{2} .$

例 4.1.8 令 $f(t)=2 t+1$ 和 $g(t)=\sqrt{1+t}$。则 $g \circ f(t)=\sqrt{1+(2 t+1)}=$ $\sqrt{2 t+2}$ 为 $t \geq-1$。如果 $t<-1$ 平方根符号的内部是负数，那么没有意义。因此，$g \circ f:{t \in \mathbb{R}: t \geq-1} \rightarrow \mathbb{R}$。

请注意，在最后一个示例中，有必要对 $g \circ f$ 的域大惊小怪，因为 $g$ 仅针对 $t$ 的某些值定义。