0 0

By admin 数学代写 2022年2月23日

There is s very useful way of thinking of continuity in terms of limits of sequences found in the following theorem. In words, it says a function is continuous if it takes convergent sequences to convergent sequences whenever possible.

Theorem 6.1.1 A function $f: D(f) \rightarrow \mathbb{F}^{q}$ is continuous at $x \in D(f) \subseteq F^{P}$ if and only if, whenever $x_{n} \rightarrow x$ with $x_{n} \in D(f)$, it follows $f\left(x_{n}\right) \rightarrow f(x)$.

Proof: Suppose first that $f$ is continuous at $x$ and let $x_{n} \rightarrow x$. Let $\varepsilon>0$ be given. By continuity, there exists $\delta>0$ such that if $|y-x|<\delta$, then $|f(x)-f(y)|<\varepsilon$. However, there exists $n_{5}$ such that if $n \geq n_{5}$, then $\left|x_{n}-x\right|<\delta$ and so for all $n$ this large, $\left|f(x)-f\left(x_{n}\right)\right|<\varepsilon$ which shows $f\left(x_{n}\right) \rightarrow f(x)$.

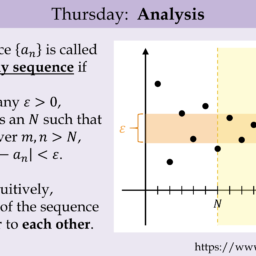
Now suppose the condition about taking convergent sequences to convergent sequences holds at $x$. Suppose $f$ fails to be continuous at $x$. Then there exists $\varepsilon>0$ and $x_{n} \in D(f)$ such that $\left|x-x_{n}\right|<\frac{1}{n}$, yet $\left|f(x)-f\left(x_{n}\right)\right| \geq \varepsilon .$ But this is clearly a contradiction because, although $x_{n} \rightarrow x, f\left(x_{n}\right)$ fails to converge to $f(x)$. It follows $f$ must be continuous after all.

Theorem 6.1.2 Suppose $f: D(f) \rightarrow \mathbb{R}$ is continuous at $x \in D(f)$ and suppose $f\left(x_{n}\right) \leq l(\geq l)$ where $\left{x_{n}\right}$ is a sequence of points of $D(f)$ which converges to $x$. Then $f(x) \leq l(\geq l) .$

Proof: Since $f\left(x_{n}\right) \leq l$ and $f$ is continuous at $x$, it follows from Theorem $4.4 .13$ and Theorem 6.1.1. $f(x)=\lim {n \rightarrow \infty} f\left(x{n}\right) \leq l$. The other case is entirely similar.
The following is a useful characterization of a continuous function which ties together many of the above conditions. I am being purposely vague about the domain of the function and its range because this theorem is a general result which holds whenever the symbols make sense and things like the triangle inequality hold.

Definition 6.1.3 Let $S$ be a nonempty set. Then one can define relatively open and relatively closed subsets of $S$ as follows. A set $U \subseteq S$ is relatively open if $U=V \cap S$ where $V$ is open. A set $C \subseteq S$ is relatively closed if there is a closed set $H$ such that $C=S \cap H$.
Proposition $6.1 .4$ Let $C \subseteq S$ where $S$ is a nonempty set. Then $C$ is relatively closed if and only if whenever $x_{n} \rightarrow x \in S$ with exch $x_{n} \in C$, it follows that $x \in C . A$ set $U \subseteq S$ is relatively open if and only if $S \backslash U$ is relatively closed.

Proof: Suppose $C$ is relatively closed. Then $C=H \cap S$ where $H$ is closed. Suppose then that $x_{n} \in C$ and $x_{n} \rightarrow x \in S$. Does it follow that $x \in C ?$ It is given that $x \in S$ so it suffices to verify that $x \in H$. However, this follows because $H$ is closed.

Conversely, suppose the limit condition for $C \subseteq S$. Why is $C$ relatively closed? What should $H$ be? Let $H$ be the set of all limits of sequences from $C$. This is clearly a closed set because if you have $h_{n} \in H$ and $h_{n} \rightarrow h$, then $B(h, 1 / m)$ contains $h_{n}$ for all $n$ large enough. Say this happens for $n \geq m_{n}$. Pick $h_{m_{n}} \in B(h, 1 / m)$ where $n \rightarrow m_{n}$ is strictly increasing. Then since the ball is open, there exists $\delta_{m}>0$ such that $B\left(h_{n_{m}}, \delta_{m}\right) \subseteq B(h, 1 / m)$. Since $h_{n_{m}}$ is a limit of some sequence from $C$, it follows there exists $\delta_{m}>0$ such that $c_{m} \in B\left(h_{n_{m}}, \delta_{m}\right) \cap C \subseteq B(h, 1 / m) \cap C$. Then $c_{m} \rightarrow h$ and $H$ is closed because it retains all limits of sequences of points from $H$. Now consider $H \cap S$. Does it contain $C$ ? Certainly. If $c \in C$, consider the constant sequence $c_{n}=c$ for all $n$. Is $H \cap S$ contained in $C ?$ If you have $h \in H \cap S$, then by definition, there is a sequence $c_{n} \rightarrow h$ where $c_{n} \in C \subseteq S$ and $h \in H \cap S$ so from the limit condition, it follows that $h \in C$. Thus the two sets are the same and $C$ is relatively closed.

The last assertion follows from the definition of open sets being the complements of closed sets and closed sets are the complements of open sets. Thus $U \subseteq S$ is relatively open if and only if $U=S \cap V$ for $V$ open if and only if $S \backslash U=S \backslash(S \cap V)$ if and only if $S \backslash U=S \backslash V \equiv S \cap V^{C}$ if and only if $S \backslash U$ is relatively closed.

Theoren $6.1 .5$ Let $f$ be a function defined on $D(f) \subseteq \mathrm{F}^{p}$. The following are equivalent.

$f$ is continuous on $D(f)$
For every $\varepsilon>0$ and $x \in D(f)$ there exists $\delta>0$ such that if $|y-x|<\delta$ and $y \in D(f)$, then $|f(x)-f(y)|<\varepsilon .$
For every $x \in D(f)$, if $x_{n} \rightarrow x$ where each $x_{n} \in D(f)$, then $f(x)=\lim {n \rightarrow \infty} f\left(x{n}\right)$.
Whenever $U$ is open, $f^{-1}(U)$ equals the intersection of an open set with $D(f)$. That is, $f^{-1}(U)$ is relatively open in $D(f)$.
Whenever $C$ is closed, $f^{-1}(C)$ is the intersection of a closed set with $D(f)$. That is, $f^{-1}(C)$ is relatively closed in $D(f)$.

Proof: To say that $f$ is continuous on $D(f)$ is to say that it is continuous at every $x \in D(f)$. Therefore, 1.) implies 2.). If 2.) holds then by definition $f$ is continuous at every $x \in D(f)$ so it is continuous on $D(f)$. Thus the first two conditions are equivalent. These are equivalent to the third condition by Theorem 6.1.1. Thus the first three conditions are equivalent.

Now suppose the fourth condition holds that “inverse images of open sets are open”. Why is $f$ continuous at $x \in D(f)$ ? This is obviously so because if you take $U=$ $B(f(x), \varepsilon)$, then $f^{-1}(B(f(x), \varepsilon))=V \cap D(f)$. Since $x \in V \cap D(f)$, it follows that there is some $\delta>0$ such that $B(x, \delta) \subseteq V$ since $V$ is open. Therefore, if $y \in$ $B(x, \delta) \cap D(f)$, it follows that $f(y) \in B(f(x), \varepsilon)$ and so in other words, if $|x-y|<\delta$ with $y \in D(f)$, then $|f(x)-f(y)|<\varepsilon .$ Hence $f$ is continuous at every $x \in D(f) .$ Thus $f$ is continuous on $D(f)$. Conversely, suppose $f$ is continuous on $D(f)$ and let $U$ be open. Consider $x \in f^{-1}(U)$. By assumption $f$ is continuous at $x$. Let $\varepsilon>0$ be such that $B(f(x), \varepsilon) \subseteq U$. Then by the definition of continuity, there exists $\delta_{x}>0$ such that if $|y-x|<\delta_{x}$ and $y \in D(f)$, then $f(y) \in B(f(x), \varepsilon)$. In other words,
$$
B\left(x, \delta_{x}\right) \cap D(f) \subseteq f^{-1}(B(f(x), \varepsilon)) \subseteq f^{-1}(U)
$$
$$
f^{-1}(U)=U_{x \in f^{-1}(U)}\left(B\left(x, \delta_{z}\right) \cap D(f)\right)=\left(U_{x \in f^{-1}(U)} B\left(x, \delta_{x}\right)\right) \cap D(f)
$$
which is the intersection of an open set with $D(f)$. Thus the first four conditions are equivalent.
Now let $C$ be closed and suppose condition 4.)
$$
f^{-1}(C) \cup f^{-1}\left(C^{C}\right)=D(f)
$$
Since every $x \in D(f)$ either has $f(x) \in C$ or $f(x) \notin C$.
$$
\left(f^{-1}(C) \cap D(f)\right) \cup\left(f^{-1}\left(C^{C}\right) \cap D(f)\right)=D(f)
$$
Now since $C^{C}$ is open, there is an open set $V$ such that $f^{-1}\left(C^{C}\right) \cap D(f)=V \cap D(f)$. Hence $f^{-1}(C) \cap D(f)=V^{C} \cap D(f)$. Thus 4.) implies 5.). Now assume 5.). Then if $C$ is closed, there is a closed set $H$ such that $f^{-1}(C) \cap D(f)=H \cap D(f)$. Then $H^{C} \cap D(f)=f^{-1}\left(C^{C}\right) \cap D(f)$ which is an open set intersected with $D(f)$. It follows, since a generic open set is of the form $C^{C}$, that 4.) holds.

Note that another way to incorporate the last two conditions is to use Proposition 6.1.4. If $f$ is continuous on $D(f)$, then if $H$ is closed, note that $f^{-1}(H)$ is relatively closed in $D(f)$ because if $x_{n} \in f^{-1}(H) \cap D(f)$ and $x_{n} \rightarrow x \in D(f)$, then by continuity $f\left(x_{n}\right) \rightarrow f(x)$ and so $f(x) \in H$ since $H$ is closed. Hence $x \in f^{-1}(H)$ so $f^{-1}(H)$ is relatively closed. If $f^{-1}(H)$ is relatively closed for all $H$ closed, and $x \in D(f)$, why is $f$ continuous at $x$ ? Say $x_{n} \rightarrow x \in D(f)$ with each $x_{n} \in D(f)$. If $f\left(x_{n}\right)$ fails to converge to $f(x)$, then there is a subsequence, still denoted as $x_{n}$ and $\delta>0$ such that $f\left(x_{n}\right) \in B(f(x), \delta)^{C}$ a closed set. Hence $f^{-1}\left(B(f(x), \delta)^{C}\right)$ must be relatively closed and $x_{n}$ is in this relatively closed set with $x_{n} \rightarrow x \in D(f)$. But this implies by Proposition $6.1 .4$ that $x \in f^{-1}\left(B(f(x), \delta)^{C}\right)$ which is a contradiction. Hence $f\left(x_{n}\right) \rightarrow f(x)$. Now inverse images of open sets being relatively open is the same ass inverse images of closed sets being relatively closed so the other of the last two conditions also is obtained.
$6.2$ Exercises

Let $f(x)=2 x+7$. Show $f$ is continuous at every point $x$. Hint: You need to let $\varepsilon>0$ be given. In this case, you should try $\delta \leq \varepsilon / 2$. Note that if one $\delta$ works in the definition, then so does any smaller $\delta$.
Suppose $D(f)=[0,1] \cup{9}$ and $f(x)=x$ on $[0,1]$ while $f(9)=5$. Is $f$ continuous at the point, 9 ? Use whichever definition of continuity you like.
Let $f(x)=x^{2}+1$. Show $f$ is continuous at $x=3$. Hint: $|f(x)-f(3)|=$ $\left|x^{2}+1-(9+1)\right|=|x+3||x-3|$. Thus if $|x-3|<1$, it follows from the triangle inequality, $|x|<1+3=4$ and so $|f(x)-f(3)|<4|x-3|$. Now try to complete the argument by letting $\delta \leq \min (1, \varepsilon / 4)$. The symbol, min means to take the minimum of the two numbers in the parenthesis.
Let $f(x)=2 x^{2}+1$. Show $f$ is continuous at $x=1$.
Let $f(x)=x^{2}+2 x$. Show $f$ is continuous at $x=2$. Then show it is continuous at every point.
Let $f(x)=|2 x+3|$. Show $f$ is continuous at every point. Hint: Review the two versions of the triangle inequality for absolute values.

在以下定理中，有一种非常有用的方法来思考连续性。换句话说，如果函数尽可能将收敛序列变为收敛序列，则它说函数是连续的。

定理 6.1.1 一个函数 $f: D(f) \rightarrow \mathbb{F}^{q}$ 在 $x \in D(f) \subseteq F^{P}$ 是连续的当且仅当，每当$x_{n} \rightarrow x$ 与 $x_{n} \in D(f)$，它遵循 $f\left(x_{n}\right) \rightarrow f(x)$。

证明：首先假设$f$ 在$x$ 处是连续的，令$x_{n} \rightarrow x$。设$\varepsilon>0$。通过连续性，存在$\delta>0$，使得如果$|y-x|<\delta$，则$|f(x)-f(y)|<\varepsilon$。但是，存在 $n_{5}$ 使得如果 $n \geq n_{5}$，那么 $\left|x_{n}-x\right|<\delta$ 等等对于所有 $n$这个大，$\left|f(x)-f\left(x_{n}\right)\right|<\varepsilon$ 显示 $f\left(x_{n}\right) \rightarrow f( x)$。

现在假设将收敛序列取为收敛序列的条件保持在 $x$。假设 $f$ 在 $x$ 处不连续。则存在 $\varepsilon>0$ 和 $x_{n} \in D(f)$ 使得 $\left|x-x_{n}\right|<\frac{1}{n}$,然而 $\left|f(x)-f\left(x_{n}\right)\right| \geq \varepsilon .$ 但这显然是矛盾的，因为尽管 $x_{n} \rightarrow x，f\left(x_{n}\right)$ 无法收敛到 $f(x)$。它遵循 $f$ 毕竟必须是连续的。

定理 6.1.2 假设 $f: D(f) \rightarrow \mathbb{R}$ 在 $x \in D(f)$ 处是连续的并且假设 $f\left(x_{n}\right) \leq l( \geq l)$ 其中 $\left{x_{n}\right}$ 是收敛到 $x$ 的 $D(f)$ 的点序列。然后 $f(x) \leq l(\geq l) .$

证明：由于 $f\left(x_{n}\right) \leq l$ 和 $f$ 在 $x$ 处是连续的，因此它遵循定理 $4.4 .13$ 和定理 6.1.1。 $f(x)=\lim {n \rightarrow \infty} f\left(x{n}\right) \leq l$。另一种情况完全类似。
以下是将上述许多条件联系在一起的连续函数的有用表征。我故意对函数的域及其范围模糊不清，因为这个定理是一个普遍的结果，只要符号有意义并且三角不等式之类的东西成立，它就成立。

定义 6.1.3 令 $S$ 是一个非空集。然后可以如下定义 $S$ 的相对开放和相对封闭的子集。如果 $U=V \cap S$ 其中 $V$ 是开放的，则集合 $U \subseteq S$ 是相对开放的。如果有一个闭集$H$ 使得$C=S \cap H$，则一个集合$C \subseteq S$ 是相对闭集。
命题 $6.1 .4$ 令 $C \subseteq S$ 其中 $S$ 是一个非空集。那么 $C$ 是相对封闭的当且仅当每当 $x_{n} \rightarrow x \in S$ 与 exch $x_{n} \in C$，它遵循 $x \in C 。 A$ set $U \subseteq S$ 是相对开放的当且仅当 $S \backslash U$ 是相对封闭的。

证明：假设$C$是相对封闭的。然后 $C=H \cap S$ 其中 $H$ 关闭。然后假设 $x_{n} \in C$ 和 $x_{n} \rightarrow x \in S$。它遵循$x \in C 吗？$ 给定$x \in S$，因此足以验证$x \in H$。但是，这是因为 $H$ 已关闭。

相反，假设 $C \subseteq S$ 的极限条件。为什么$C$相对封闭？ $H$ 应该是什么？令 $H$ 是来自 $C$ 的所有序列限制的集合。这显然是一个封闭集，因为如果你有 $h_{n} \in H$ 和 $h_{n} \rightarrow h$，那么 $B(h, 1 / m)$ 包含所有 $h_{n}$ $n$ 足够大。假设这发生在 $n \geq m_{n}$ 上。选择 $h_{m_{n}} \in B(h, 1 / m)$ 其中 $n \rightarrow m_{n}$ 严格递增。那么由于球是开放的，存在 $\delta_{m}>0$ 使得 $B\left(h_{n_{m}}, \delta_{m}\right) \subseteq B(h, 1 / m )$。由于 $h_{n_{m}}$ 是来自 $C$ 的某个序列的极限，因此存在 $\delta_{m}>0$ 使得 $c_{m} \in B\left(h_{n_ {m}}, \delta_{m}\right) \cap C \subseteq B(h, 1 / m) \cap C$。然后 $c_{m} \rightarrow h$ 和 $H$ 是闭合的，因为它保留了来自 $H$ 的点序列的所有限制。现在考虑 $H \cap S$。它是否包含 $C$ ？当然。如果$c \in C$，考虑所有$n$ 的常数序列$c_{n}=c$。 $H \cap S$ 是否包含在 $C 中？$ 如果你有 $h \in H \cap S$，那么根据定义，有一个序列 $c_{n} \rightarrow h$ where $c_{n} \在 C \subseteq S$ 和 $h \in H \cap S$ 所以从极限条件，它遵循 $h \in C$。因此这两个集合是相同的，$C$ 是相对封闭的。

最后一个断言来自开集的定义是闭集的补集，闭集是开集的补集。因此 $U \subseteq S$ 是相对开放的当且仅当 $U=S \cap V$ 对 $V$ 开放当且仅当 $S \backslash U=S \backslash(S \cap V)$ 当且仅if $S \backslash U=S \backslash V \equiv S \cap V^{C}$ 当且仅当 $S \backslash U$ 是相对封闭的。

定理 $6.1 .5$ 令 $f$ 是定义在 $D(f) \subseteq \mathrm{F}^{p}$ 上的函数。以下是等价的。