数学代写| Changes in the Objective Coefficients 凸优化代考代写 - 代考代写：100%准时可靠您的作业代写专家

0 0

By admin 数学代写 2022年3月7日

代写隐藏

1 数学代写| Changes in the Objective Coefficients 凸优化代考

数学代写| Changes in the Objective Coefficients 凸优化代考

凸优化代写

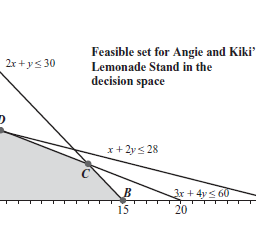
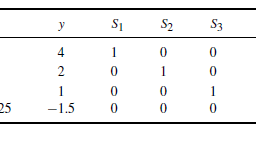
Consider the lemonade stand problem from Chapter 3 . We know the optimal solution to the problem is given by the following:
$$
\begin{aligned}
x &=12 \text { glasses sweet lemonade } \
y &=6 \text { glasses tart lemonade } \
R &=\$ 24.00 \text { (maximized) } \
S_{1} &=0 \text { leftover lemons } \
S_{2} &=4 \text { leftover limes } \
S_{3} &=0 \text { leftover tablespoons sugar. }
\end{aligned}
$$
Sensitivity analysis is the study of how sensitive this solution is to minor changes in the original problem. For example, suppose we change the price of a glass of tart lemonade from $\$ 1.50$ to
$4.1$ Introduction to Sensitivity Analysis 149
$\$ 1.55$, with no other changes to the problem. What will the new solution be? Will $(12,6)$ still represent the optimal solution, or will the optimal values of the decision variables change to a different corner of the feasible set? How will the values of the slack variables change, and what will the optimal revenue change to?

We can ask similar questions with regard to any small change to the problem. Instead of changing the price of a glass of lemonade, we can ask what would happen to the solution if our supply of lemons changed from 60 to 65 , or if our supply of sugar decreased from 30 tablespoons to 20 . What if it was possible to increase the supply of just one of the resources – lemons, limes, or sugar? How can we measure which resource is the most valuable?

We could even address small changes in the recipes of the lemonade itself if we so desired. Suppose we used $3.5$ lemons per glass of tart lemonade instead of four? How would this affect the optimal solution? Certainly, it would be useful for Angie and Kiki to know all of this information, in case they are considering changes to their lemonade stand operation.

Now, to answer any of these questions, one way to proceed would be to simply solve the problem again with the changed information. But that can be rather tedious, and the point of sensitivity analysis is to extract useful information without having to solve the entire problem over again. The ease of extracting this type of useful information depends on the technique used to solve the problem. Doing sensitivity analysis with algebraic methods such as the simplex algorithm (which we cover in the next chapter) is generally more effective and easier than with graphical (which we cover in the next chapter) is generally more effective and easier than with graphical methods. So we will revisit these ideas later after the simplex algorithm is introduced.
Let us divide the type of questions we could ask into several distinct categories:

Changes in the objective coefficients. Here we consider what happens to the optimal solution if the only change we make is to one coefficient of the objective function. In the lemonade stand problem, this means changing the price of a glass of sweet lemonade or the price of a glass of tart lemonade.
Changes in the capacity. This refers to what happens when we change one of the numbers on the right-hand side of one of the inequalities that define the feasible set. In the lemonade stand problem, this means changing the amount of one of the resources – lemons, limes, or sugar. The capacity to make lemonade obviously depends on how much of these resources we have available to allocate, explaining why we call this “changes in the capacity.”
The marginal value associated with a constraint. The exact definition of marginal value appears in Section 4.3. In the lemonade stand problem, the constraints arise from the resources – lemons, limes, and sugar. So each resource will have a marginal value that helps answer the question we raised earlier of which resource is the most valuable at a given corner point.
Structural changes. This refers to what happens when we change one coefficient on the left-hand side of one of the constraints. In the lemonade stand problem, this means we are changing the amount of one of the resources in the recipe of one of the types lemone. Another possible structural change would be the addition of a new decision variable. In the lemonade stand problem, this refers to situation where the girls start selling a third type of lemonade – for example, a lite lemonade with low sugar content.

The first three of these types of questions are commonly studied in most textbooks. Structural changes, the fourth type, are less frequently addressed, but we mention these changes in the context of sensitivity analysis for the sake of completeness.

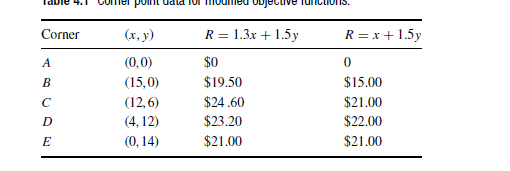
凸优化代考

考虑第 3 章中的柠檬水摊问题。我们知道该问题的最佳解决方案如下：
$$
\开始{对齐}
x &=12 \text { 杯甜柠檬水 } \
y &=6 \text { 玻璃挞柠檬水 } \
R &=\$ 24.00 \text { (最大化) } \
S_{1} &=0 \text { 剩下的柠檬 } \
S_{2} &=4 \text { 剩下的酸橙 } \
S_{3} &=0 \text { 剩下的汤匙糖。 }
\end{对齐}
$$
敏感性分析是研究该解决方案对原始问题的微小变化的敏感性。例如，假设我们将一杯酸柠檬水的价格从 $\$ 1.50$ 更改为
$4.1$ 敏感性分析简介 149
$\$ 1.55$，问题没有其他变化。新的解决方案将是什么？ $(12,6)$ 是否仍然代表最优解，或者决策变量的最优值会改变到可行集的不同角落？松弛变量的值将如何变化，最佳收入将如何变化？

对于问题的任何微小变化，我们都可以提出类似的问题。与其改变一杯柠檬水的价格，我们可以询问如果我们的柠檬供应量从 60 变为 65 ，或者如果我们的糖供应量从 30 汤匙减少到 20 ，解决方案会发生什么。如果可以增加其中一种资源的供应——柠檬、酸橙或糖，会怎样？我们如何衡量哪种资源最有价值？

如果我们愿意，我们甚至可以解决柠檬水配方本身的微小变化。假设我们每杯酸柠檬水使用 3.5 美元的柠檬而不是四杯？这将如何影响最佳解决方案？当然，如果 Angie 和 Kiki 正在考虑改变他们的柠檬水摊运营，了解所有这些信息会很有用。

现在，要回答这些问题中的任何一个，一种方法是使用更改的信息再次简单地解决问题。但这可能相当乏味，敏感性分析的重点是提取有用的信息，而不必重新解决整个问题。提取此类有用信息的难易程度取决于用于解决问题的技术。使用诸如单纯形算法（我们将在下一章中介绍）之类的代数方法进行敏感性分析通常比使用图形（我们将在下一章中介绍）更有效和更容易，通常比使用图形方法更有效和更容易。所以我们稍后会在介绍单纯形算法后重新审视这些想法。
让我们将我们可以提出的问题类型分为几个不同的类别：

客观系数的变化。在这里，我们考虑如果我们所做的唯一改变是目标函数的一个系数，那么最优解会发生什么。在柠檬水摊问题中，这意味着改变一杯甜柠檬水的价格或一杯酸柠檬水的价格。
容量的变化。这是指当我们更改定义可行集的不等式之一右侧的数字之一时会发生什么。在柠檬水摊问题中，这意味着改变其中一种资源的数量——柠檬、酸橙或糖。制造柠檬水的能力显然取决于我们有多少资源可以分配，这解释了为什么我们称之为“能力变化”。
与约束相关的边际价值。边际价值的确切定义出现在第 4.3 节。在柠檬水摊问题中，限制来自资源——柠檬、酸橙和糖。因此，每种资源都有一个边际价值，这有助于回答我们之前提出的问题，即在给定的角落点哪种资源最有价值。
结构变化。这是指当我们改变其中一个约束左侧的一个系数时会发生什么。在柠檬水摊问题中，这意味着我们正在改变其中一种柠檬的配方中一种资源的数量。另一个可能的结构变化是增加一个新的决策变量。在柠檬水摊问题中，这指的是女孩们开始销售第三种柠檬水的情况——例如，低糖的清淡柠檬水。

大多数教科书通常都会研究这些类型的前三种问题。第四种类型的结构变化很少被提及，但为了完整起见，我们在敏感性分析的背景下提到这些变化。