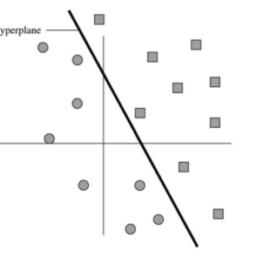
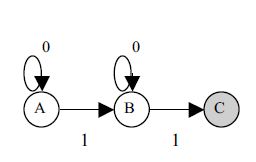
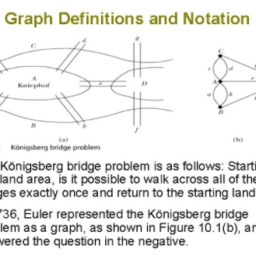
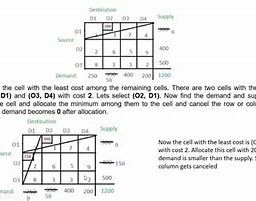
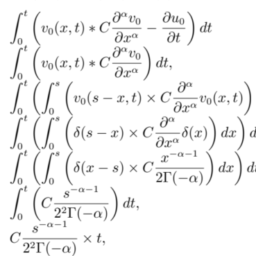运筹学(Operation)是近代应用数学的一个分支。它把具体的问题进行数学抽象,然后用像是统计学、数学模型和算法等方法加以解决,以此来寻找复杂问题中的最佳或近似最佳的解答。
作为专业的留学生服务机构,Assignmentexpert™多年来已为美国、英国、加拿大、澳洲等留学热门地的学生提供专业的学术服务,包括但不限于论文代写,A作业代写,Dissertation代写,Report代写,Paper代写,Presentation代写,网课代修等等。为涵盖高中,本科,研究生等海外留学生提供辅导服务,辅导学科包括数学,物理,统计,化学,金融,经济学,会计学等全球99%专业科目。写作团队既有专业英语母语作者,也有海外名校硕博留学生,每位写作老师都拥有过硬的语言能力,专业的学科背景和学术写作经验。我们承诺100%原创,100%专业,100%准时,100%满意。
my-assignmentexpert愿做同学们坚强的后盾,助同学们顺利完成学业,同学们如果在学业上遇到任何问题,请联系my-assignmentexpert™,我们随时为您服务!
运筹学代写
There is an algorithm, termed the Homogeneous Self-Dual Algorithm that overcomes the difficulties mentioned above. The algorithm achieves the theoretically best $O(\sqrt{n} \log (1 / \varepsilon))$ complexity bound and is often used in linear programming software packages.
The algorithm is based on the construction of a homogeneous and self-dual linear program related to (LP) and (LD) (see Sect. 5.5). We now briefly explain the two major concepts, homogeneity and self-duality, used in the construction.
In general, a system of linear equations of inequalities is homogeneous if the right hand side components are all zero. Then if a solution is found, any positive multiple of that solution is also a solution. In the construction used below, we allow a single inhomogeneous constraint, often called a normalizing constraint. Karmarkar’s original canonical form is a homogeneous linear program.
A linear program is termed self-dual if the dual of the problem is equivalent to the primal. The advantage of self-duality is that we can apply a primal-dual interiorpoint algorithm to solve the self-dual problem without doubling the dimension of the linear system solved at each iteration.
$5.7$ Termination and Initialization
157
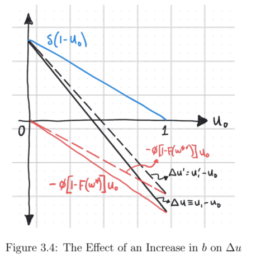
The homogeneous and self-dual linear program (HSDP) is constructed from (LP) and (LD) in such a way that the point $\mathbf{x}=\mathbf{1}, \mathbf{y}=\mathbf{0}, \tau=1, z=1, \theta=1$ is feasible. The primal program is where $$ \overline{\mathbf{b}}=\mathbf{b}-\mathbf{A l}, \overline{\mathbf{c}}=\mathbf{c}-\mathbf{1}, \bar{z}=\mathbf{c}^{T} \mathbf{1}+1 $$
Note also that the top two constraints in (HSDP), with $\tau=1$ and $\theta=0$, represent primal and dual feasibility (with $\mathbf{x} \geq \mathbf{0}$ ). The third equation represents reversed weak duality (with $\mathbf{b}^{T} \mathbf{y} \geq \mathbf{c}^{T} \mathbf{x}$ ) rather than the reverse. So if these three equations are satisfied with $\tau=1$ and $\theta=0$ they define primal and dual optimal solutions. Then, to achieve primal and dual feasibility for $\mathbf{x}=\mathbf{1},(\mathbf{y}, \mathbf{s})=(\mathbf{0}, \mathbf{1})$, we artificial variable $\theta$. The fourth constraint is added to achieve self-duality.
The problem is self-dual because its overall coefficient matrix has the property that its transpose is equal to its negative. It is skew-symmetric.
Denote by $\mathbf{s}$ the slack vector for the second constraint and by $\kappa$ the slack scalar for the third constraint. Denote by $\mathcal{F}{h}$ the set of all points $(\mathbf{y}, \mathbf{x}, \tau, \theta, \mathbf{s}, \kappa)$ that are feasible for (HSDP). Denote by $\mathcal{F}{h}^{0}$ the set of strictly feasible points with $(\mathbf{x}, \boldsymbol{\tau}, \mathbf{s}, \boldsymbol{\kappa})>\mathbf{0}$ in $\mathcal{F}_{h}$. By combining the constraints (Exercise 14) we can write the last (equality) constraint as
$$
\mathbf{1}^{T} \mathbf{x}+\mathbf{1}^{T} \mathbf{s}+\tau+\kappa-(n+1) \theta=(n+1)
$$
which serves as a normalizing constraint for (HSDP). This implies that for $0 \leq \theta \leq$ 1 the variables in this equation are bounded.
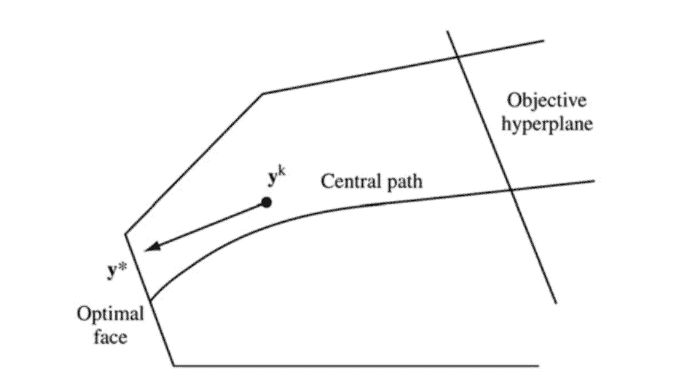
有一种算法,称为同质自对偶算法,它克服了上述困难。该算法实现了理论上最佳的$O(\sqrt{n} \log (1 / \varepsilon))$ 复杂度界限,常用于线性编程软件包。
该算法基于与 (LP) 和 (LD) 相关的齐次和自对偶线性程序的构造(参见第 5.5 节)。我们现在简要解释在构造中使用的两个主要概念,同质性和自我对偶性。
通常,如果右侧分量均为零,则不等式线性方程组是齐次的。然后,如果找到解决方案,则该解决方案的任何正倍数也是一个解决方案。在下面使用的构造中,我们允许单个非均匀约束,通常称为规范化约束。 Karmarkar 的原始规范形式是齐次线性规划。
如果问题的对偶等价于原始问题,则线性程序称为自对偶。自对偶的优点是我们可以应用原始对偶内点算法来解决自对偶问题,而无需在每次迭代中将求解的线性系统的维数加倍。
$5.7$ 终止和初始化
157
齐次自对偶线性规划 (HSDP) 由 (LP) 和 (LD) 构成,使得点 $\mathbf{x}=\mathbf{1}, \mathbf{y}=\mathbf{ 0}, \tau=1, z=1, \theta=1$ 是可行的。原始程序是 $$ \overline{\mathbf{b}}=\mathbf{b}-\mathbf{A l}, \overline{\mathbf{c}}=\mathbf{c}-\mathbf{1 }, \bar{z}=\mathbf{c}^{T} \mathbf{1}+1 $$
还要注意(HSDP)中的前两个约束,$\tau=1$ 和 $\theta=0$,代表原始和双重可行性($\mathbf{x} \geq \mathbf{0}$)。第三个等式表示反向的弱对偶(与 $\mathbf{b}^{T} \mathbf{y} \geq \mathbf{c}^{T} \mathbf{x}$ )而不是相反。因此,如果这三个方程满足 $\tau=1$ 和 $\theta=0$,它们就定义了原始最优解和对偶最优解。然后,为了实现 $\mathbf{x}=\mathbf{1},(\mathbf{y}, \mathbf{s})=(\mathbf{0}, \mathbf{1})$ 的原始和双重可行性,我们人为变量$\theta$。添加第四个约束以实现自我对偶。
这个问题是自对偶的,因为它的整体系数矩阵具有它的转置等于它的负数的性质。它是斜对称的。
用 $\mathbf{s}$ 表示第二个约束的松弛向量,用 $\kappa$ 表示第三个约束的松弛标量。用 $\mathcal{F}{h}$ 表示所有点 $(\mathbf{y}, \mathbf{x}, \tau, \theta, \mathbf{s}, \kappa)$ 的集合,它们是可行的(HSDP)。用 $\mathcal{F}{h}^{0}$ 表示严格可行点的集合 $(\mathbf{x}, \boldsymbol{\tau}, \mathbf{s}, \boldsymbol{\kappa })>\mathbf{0}$ in $\mathcal{F}_{h}$。通过组合约束(练习 14),我们可以将最后一个(等式)约束写为
$$
\mathbf{1}^{T} \mathbf{x}+\mathbf{1}^{T} \mathbf{s}+\tau+\kappa-(n+1) \theta=(n+1)
$$
作为 (HSDP) 的规范化约束。这意味着对于 $0 \leq \theta \leq$ 1,这个方程中的变量是有界的。
运筹学代考

什么是运筹学代写
运筹学(OR)是一种解决问题和决策的分析方法,在组织管理中很有用。在运筹学中,问题被分解为基本组成部分,然后通过数学分析按定义的步骤解决。
运筹学的过程大致可以分为以下几个步骤:
- 确定需要解决的问题。
- 围绕问题构建一个类似于现实世界和变量的模型。
- 使用模型得出问题的解决方案。
- 在模型上测试每个解决方案并分析其成功。
- 实施解决实际问题的方法。
与运筹学交叉的学科包括统计分析、管理科学、博弈论、优化理论、人工智能和复杂网络分析。所有这些学科的目标都是解决某一个现实中出现的复杂问题或者用数学的方法为决策提供指导。 运筹学的概念是在二战期间由参与战争的数学家们提出的。二战后,他们意识到在运筹学中使用的技术也可以被应用于解决商业、政府和社会中的问题。
运筹学代写的三个特点
所有运筹学解决实际问题的过程中都具有三个主要特征:
- 优化——运筹学的目的是在给定的条件下达到某一机器或者模型的最佳性能。优化还涉及比较不同选项和缩小潜在最佳选项的范围。
- 模拟—— 这涉及构建模型,以便在应用解决方案刀具体的复杂大规模问题之前之前尝试和测试简单模型的解决方案。
- 概率和统计——这包括使用数学算法和数据挖掘来发现有用的信息和潜在的风险,做出有效的预测并测试可能的解决方法。
运筹学领域提供了比普通软件和数据分析工具更强大的决策方法。此外,运筹学可以根据特定的业务流程或用例进行定制,以确定哪些技术最适合解决问题。
运筹学可以应用于各种活动,比如:计划和时间管理(Planning and Time Management),城乡规划(Urban and Rural Planning),企业资源计划(ERP)与供应链管理(Supply Chain Management)等等。 如有代写代考需求,欢迎同学们联系Assignmentexpert™,我们期待为你服务!