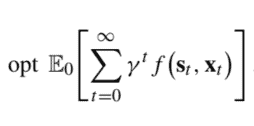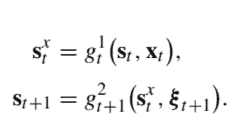如果你也在为遇到的matlab相关的难题发愁,请随时右上角联系我们的24/7代写客服。MATLAB®将为迭代分析和设计过程而调整的桌面环境与直接表达矩阵和阵列数学的编程语言相结合。它包括用于创建脚本的实时编辑器,这些脚本将代码、输出和格式化文本结合在可执行的笔记本中。
- 专业构建
MATLAB工具箱是专业开发的,经过严格的测试,并有完整的文件记录。 - 拥有互动式应用程序
MATLAB应用程序让您看到不同的算法是如何与您的数据一起工作的。迭代直到您得到您想要的结果,然后自动生成一个MATLAB程序来重现或自动完成您的工作。 - 以及扩展的能力
只需稍加修改代码,就可以将您的分析扩展到集群、GPU和云上运行。不需要重写你的代码或学习大数据编程和内存外技术。
my-assignmentexpert™ matlab作业代写,免费提交作业要求, 满意后付款,成绩80\%以下全额退款,安全省心无顾虑。专业硕 博写手团队,所有订单可靠准时,保证 100% 原创。my-assignmentexpert™, 最高质量的matlab作业代写作业代写,服务覆盖北美、欧洲、澳洲等 国家。 在代写价格方面,考虑到同学们的经济条件,在保障代写质量的前提下,我们为客户提供最合理的价格。 由于统计Statistics作业种类很多,同时其中的大部分作业在字数上都没有具体要求,因此matlab作业代写作业代写的价格不固定。通常在matlab专家查看完作业要求之后会给出报价。作业难度和截止日期对价格也有很大的影响。
想知道您作业确定的价格吗? 免费下单以相关学科的专家能了解具体的要求之后在1-3个小时就提出价格。专家的 报价比上列的价格能便宜好几倍。
my-assignmentexpert™ 为您的留学生涯保驾护航 在matlab作业代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的应用数学applied math代写服务。我们的专家在matlab作业代写方面经验极为丰富,各种matlab作业代写相关的作业也就用不着 说。
我们提供的matlab作业代写及其相关学科的代写,服务范围广, 其中包括但不限于:
- 数据分析
- 数值与符号计算
- 工程与科学绘图
- 控制系统设计
- 航天工业
- 汽车工业
- 生物医学工程
- 语音处理
运筹学代写
数学代写|matlab作业代写|What Is Dynamic Programming?
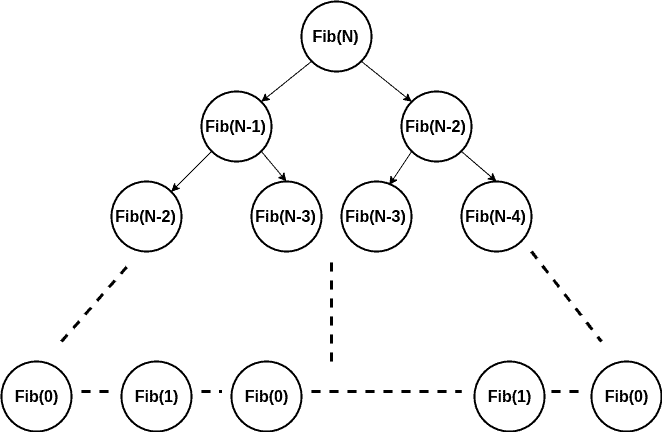
Dynamic programming is a widely used optimization approach, but it is not an algorithm. We can buy a software implementation of, say, the celebrated simplex algorithm for linear programming, but we cannot buy a software package for generic dynamic programming. ${ }^{1}$ Dynamic programming is a remarkably general and flexible principle that, among other things, may be used to design a range of optimization algorithms. The core idea hinges on the decomposition of a multistage, dynamic decision problem into a sequence of simpler, single-stage problems.
Dynamic programming, as the name suggests, is relevant to dynamic decision making over time. As we shall see, we may sometimes find it convenient to decompose a static decision problem as a sequence of intertwined decisions, in order to apply dynamic programming. For instance, this may yield efficient solution approaches for some combinatorial optimization problems where time does not really play any role. The relevant keyword, however, is multistage. A multistage decision problem should not be confused with a multiperiod decision problem. As we better illustrate in the following sections, in a finite-horizon problem we have to select $T$ decisions $\mathbf{x}_{t}$ that will be applied at a sequence of time instants $t=0,1,2, \ldots, T-1$. However, when are those decisions made? In a deterministic problem, we can make all decisions at time $t=0$, and then implement the plan over time. This corresponds to a static, multiperiod problem. The problem is static in the sense that, once we come up with a plan, we shall not revise it over time on the basis of contingencies. By doing so, in control engineering parlance, we are pursuing an open-loop approach. However, in a stochastic problem, where uncertain risk factors are involved, this rigid strategy may result in a quite poor performance, or even turn out to be infeasible with respect to constraints. In a multistage problem, we observe over time a sample path of the relevant risk factors and adapt decisions along the way. What we need is a strategy, i.e., a recipe to make decisions after observing random realizations ${ }^{2}$ of risk factors and their impact on the system state. In control engineering terms, a multistage approach is closed-loop, and decisions are a function of the observed states.
The concept of system state is central to dynamic programming, and we need a mathematical model representing its evolution over time, as a function of decisions and additional external inputs. Decisions are under our control, whereas external inputs correspond to the impact of the outside world on the system that we are managing. In a stochastic setting, external inputs correspond to random risk factors; in a deterministic one, they could be known functions of time. Dynamic programming is not a universal approach, since its application requires some specific structure in the system model. Essentially, the state of the system at time $t+1$ should depend on the state observed at time $t$, the decision made at time $t$ after observing the state, and the realization of external inputs during the subsequent time interval. However, this evolution cannot be fully path-dependent, i.e., it should not depend on the full sample path ${ }^{3}$ of states and external factors up to time $t$. A system with this property features a limited amount of memory and, as we shall see, is called Markovian.
Despite this limitation, the dynamic programming approach is the most general optimization principle at our disposal and can be applied to a wide range of problems:
- Continuous and discrete problems, where the discrete/continuous feature may refer to:
- state variables,
- decision variables,
- the representation of time.
- Deterministic and stochastic problems.
- Finite- and infinite-horizon problems.
Within the resulting wide collection of problems, we may need to solve finiteas well as infinite-dimensional problems and, for some problem structures, DP is actually the only viable solution approach. Unfortunately, as a free lunch is nowhere to be found, power and generality must come at some price. As we have remarked, DP is a principle, and its implementation for a specific problem may require a considerable customization effort. Furthermore, the literal application of DP may be impractical because of the so-called curse of dimensionality. As we shall see, there are actually multiple forms of curse that affect DP. The bottom line is that, more often than not, conventional dynamic programming is computationally overly expensive and can only be applied to rather small-scale problems. Nevertheless, we do have approximation strategies at our disposal, which may enable us to overcome the limitations of a straightforward DP approach.
Besides its flexibility in dealing with a wide array of optimization problems, DP may be applied in quite different ways:
- It may be applied literally, in order to solve an optimization problem exactly. This is feasible for small scale problems, or for problems with a specific structure. The value of solving small-sized problem instances should not be underestimated, as it may provide a convenient benchmark to assess the quality of alternative approximate approaches, which may be easier to scale up.
- It may be applied as a component of another optimization approach. For instance, in column generation algorithms for large-scale discrete optimization, DP is often used to solve column generation subproblems. ${ }^{4}$
- It may be applied in an approximate form, to devise high-quality heuristics that may be validated by computer simulation experiments. A notable and wellknown example is reinforcement learning. Sampling, by online experimentation or by Monte Carlo simulation, plays a prominent role in this respect, together with function approximation architectures, ranging from linear regression to neural networks.
- It may be applied to prove that the optimal decision strategy for a given problem has a specific form. This means that maybe we cannot easily find the numerical values that define an optimal strategy, but we may use DP to infer its structure. The structure of an optimal policy may be characterized in different ways but, sometimes, we may be able to come up with an optimal decision rule depending on a small set of unknown parameters. This paves the way to the development of near-optimal strategies, which are found by looking for a good setting of the policy parameters (an approach known as approximation in the policy space).
DP is not only a useful tool to keep ready in our pockets, but also an intellectually stimulating and rewarding concept to learn, as it requires merging ideas from an array of different sources, like stochastic modeling, statistical sampling, machine learning, numerical analysis, practical optimization, and (last but definitely not least) specific knowledge pertaining to each application domain.
matlab代写
数学代写|MATLAB作业代写|WHAT IS DYNAMIC PROGRAMMING?
动态规划是一种广泛使用的优化方法,但它不是一种算法。我们可以购买著名的线性规划单纯形算法的软件实现,但我们不能购买通用动态规划的软件包。1动态规划是一个非常普遍和灵活的原则,除其他外,它可用于设计一系列优化算法。核心思想取决于将多阶段动态决策问题分解为一系列更简单的单阶段问题。
顾名思义,动态规划与随时间的动态决策相关。正如我们将看到的,我们有时会发现将静态决策问题分解为一系列相互交织的决策以应用动态规划很方便。例如,这可能会为一些时间并不真正发挥任何作用的组合优化问题产生有效的解决方法。然而,相关的关键字是多级的。多阶段决策问题不应与多阶段决策问题相混淆。正如我们在以下部分中更好地说明的那样,在有限范围问题中,我们必须选择吨决定X吨将在一系列时间瞬间应用吨=0,1,2,…,吨−1. 然而,这些决定是什么时候做出的?在确定性问题中,我们可以同时做出所有决定吨=0,然后随着时间的推移实施计划。这对应于一个静态的多周期问题。从某种意义上说,问题是静态的,一旦我们制定了计划,我们将不会根据意外情况随着时间的推移对其进行修改。通过这样做,用控制工程的说法,我们正在追求一种开环方法。然而,在涉及不确定风险因素的随机问题中,这种僵化的策略可能会导致性能非常差,甚至在约束方面变得不可行。在多阶段问题中,我们随着时间的推移观察相关风险因素的样本路径,并在此过程中调整决策。我们需要的是一种策略,即观察随机实现后做出决策的方法2风险因素及其对系统状态的影响。在控制工程术语中,多阶段方法是闭环的,决策是观察到的状态的函数。
系统状态的概念是动态规划的核心,我们需要一个数学模型来表示其随时间的演变,作为决策和额外外部输入的函数。决策在我们的控制之下,而外部输入对应于外部世界对我们管理的系统的影响。在随机环境中,外部输入对应于随机风险因素;在确定性的情况下,它们可以是时间的已知函数。动态编程不是一种通用方法,因为它的应用需要系统模型中的某些特定结构。本质上,系统当时的状态吨+1应该取决于当时观察到的状态吨,当时做出的决定吨观察状态后,在随后的时间间隔内实现外部输入。然而,这种演变不能完全依赖于路径,即它不应该依赖于完整的样本路径3最新的状态和外部因素吨. 具有此属性的系统具有有限的内存量,正如我们将看到的,称为马尔可夫系统。
尽管有这个限制,动态规划方法是我们可以使用的最通用的优化原则,可以应用于广泛的问题:
- 连续和离散问题,其中离散/连续特征可能指:
- 状态变量,
- 决策变量,
- 时间的表示。
- 确定性和随机性问题。
- 有限和无限范围问题。
在由此产生的大量问题中,我们可能需要解决有限维和无限维问题,对于某些问题结构,DP 实际上是唯一可行的解决方法。不幸的是,由于找不到免费的午餐,权力和普遍性必须付出一定的代价。正如我们所说,DP 是一个原则,它针对特定问题的实现可能需要大量的定制工作。此外,由于所谓的维度灾难,DP 的字面应用可能是不切实际的。正如我们将看到的,实际上有多种形式的诅咒会影响 DP。最重要的是,传统的动态规划通常在计算上过于昂贵,并且只能应用于相当小规模的问题。尽管如此,
除了处理各种优化问题的灵活性之外,DP 还可以以完全不同的方式应用:
- 它可以按字面意思应用,以便准确地解决优化问题。这对于小规模问题或具有特定结构的问题是可行的。不应低估解决小型问题实例的价值,因为它可以提供一个方便的基准来评估替代近似方法的质量,这可能更容易扩大规模。
- 它可以用作另一种优化方法的组成部分。例如,在大规模离散优化的列生成算法中,DP 通常用于解决列生成子问题。4
- 它可以以近似的形式应用,以设计可以通过计算机模拟实验验证的高质量启发式方法。一个著名且众所周知的例子是强化学习。通过在线实验或蒙特卡洛模拟进行采样,以及从线性回归到神经网络的函数逼近架构,在这方面发挥着重要作用。
- 它可以用来证明给定问题的最优决策策略具有特定的形式。这意味着我们可能无法轻易找到定义最优策略的数值,但我们可以使用 DP 来推断其结构。最优策略的结构可能以不同的方式表征,但有时,我们可能能够根据一小组未知参数提出最优决策规则。这为开发近乎最优的策略铺平了道路,通过寻找策略参数的良好设置来找到这些策略一种n一种ppr○一种CH到n○在n一种s一种ppr○X一世米一种吨一世○n一世n吨H和p○一世一世C和sp一种C和.
DP 不仅是一个有用的工具,可以放在我们的口袋里,而且还是一个智力刺激和有益的学习概念,因为它需要合并来自不同来源的想法,如随机建模、统计抽样、机器学习、数值分析、实际优化,以及一世一种s吨b你吨d和F一世n一世吨和一世和n○吨一世和一种s吨与每个应用领域相关的特定知识。

统计代考
统计是汉语中的“统计”原有合计或汇总计算的意思。 英语中的“统计”(Statistics)一词来源于拉丁语status,是指各种现象的状态或状况。
数论代考
数论(number theory ),是纯粹数学的分支之一,主要研究整数的性质。 整数可以是方程式的解(丢番图方程)。 有些解析函数(像黎曼ζ函数)中包括了一些整数、质数的性质,透过这些函数也可以了解一些数论的问题。 透过数论也可以建立实数和有理数之间的关系,并且用有理数来逼近实数(丢番图逼近)
数值分析代考
数值分析NumericalAnalysis,又名“计算方法”,是研究分析用计算机求解数学计算问题的数值计算方法及其理论的学科。 它以数字计算机求解数学问题的理论和方法为研究对象,为计算数学的主体部分。
随机过程代写
随机过程,是依赖于参数的一组随机变量的全体,参数通常是时间。 随机变量是随机现象的数量表现,其取值随着偶然因素的影响而改变。 例如,某商店在从时间t0到时间tK这段时间内接待顾客的人数,就是依赖于时间t的一组随机变量,即随机过程
MATLAB代写
MATLAB 是一种用于技术计算的高性能语言。它将计算、可视化和编程集成在一个易于使用的环境中,其中问题和解决方案以熟悉的数学符号表示。典型用途包括:数学和计算算法开发建模、仿真和原型制作数据分析、探索和可视化科学和工程图形应用程序开发,包括图形用户界面构建MATLAB 是一个交互式系统,其基本数据元素是一个不需要维度的数组。这使您可以解决许多技术计算问题,尤其是那些具有矩阵和向量公式的问题,而只需用 C 或 Fortran 等标量非交互式语言编写程序所需的时间的一小部分。MATLAB 名称代表矩阵实验室。MATLAB 最初的编写目的是提供对由 LINPACK 和 EISPACK 项目开发的矩阵软件的轻松访问,这两个项目共同代表了矩阵计算软件的最新技术。MATLAB 经过多年的发展,得到了许多用户的投入。在大学环境中,它是数学、工程和科学入门和高级课程的标准教学工具。在工业领域,MATLAB 是高效研究、开发和分析的首选工具。MATLAB 具有一系列称为工具箱的特定于应用程序的解决方案。对于大多数 MATLAB 用户来说非常重要,工具箱允许您学习和应用专业技术。工具箱是 MATLAB 函数(M 文件)的综合集合,可扩展 MATLAB 环境以解决特定类别的问题。可用工具箱的领域包括信号处理、控制系统、神经网络、模糊逻辑、小波、仿真等。