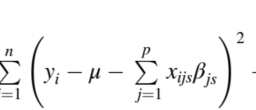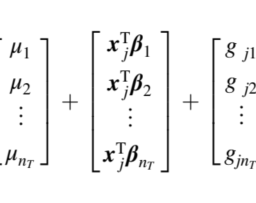如果你也在 怎样代写统计机器学习Statistical Machine Learning这个学科遇到相关的难题,请随时右上角联系我们的24/7代写客服。统计机器学习Statistical Machine Learning将统计学与计算科学–计算机科学、系统科学和优化相结合。统计机器学习的大部分议程是由科学和技术领域的应用问题驱动的,这些领域的数据流越来越大规模、动态和异质性,需要数学和算法的创造性来发挥统计方法的作用。生物信息学、人工智能、信号处理、通信、网络、信息管理、金融、博弈论和控制论等领域都受到了统计机器学习发展的极大影响。
统计机器学习领域也提出了现代统计学中一些最具挑战性的理论问题,其中最主要的是理解推理和计算之间的联系这一普遍问题。统计学习理论是一个从统计学和函数分析领域汲取的机器学习框架。统计学习理论处理的是基于数据寻找预测函数的统计推理问题。
my-assignmentexpert™统计机器学习Statistical Machine Learning作业代写,免费提交作业要求, 满意后付款,成绩80\%以下全额退款,安全省心无顾虑。专业硕 博写手团队,所有订单可靠准时,保证 100% 原创。my-assignmentexpert™, 最高质量的运筹学Operations Research作业代写,服务覆盖北美、欧洲、澳洲等 国家。 在代写价格方面,考虑到同学们的经济条件,在保障代写质量的前提下,我们为客户提供最合理的价格。 由于统计Statistics作业种类很多,同时其中的大部分作业在字数上都没有具体要求,因此运筹学Operations Research作业代写的价格不固定。通常在经济学专家查看完作业要求之后会给出报价。作业难度和截止日期对价格也有很大的影响。
想知道您作业确定的价格吗? 免费下单以相关学科的专家能了解具体的要求之后在1-3个小时就提出价格。专家的 报价比上列的价格能便宜好几倍。
my-assignmentexpert™ 为您的留学生涯保驾护航 在统计机器学习Statistical Machine Learning作业代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的应用数学applied math代写服务。我们的专家在统计机器学习Statistical Machine Learning代写方面经验极为丰富,各种统计机器学习Statistical Machine Learning相关的作业也就用不着 说。
我们提供的统计机器学习Statistical Machine Learning及其相关学科的代写,服务范围广, 其中包括但不限于:
- 商业分析 Business Analysis
- 计算机科学 Computer Science
- 数据挖掘/数据科学/大数据 Data Mining / Data Science / Big Data
- 决策分析 Decision Analytics
- 金融工程 Financial Engineering
- 数据预测 Data Forecasting
- 博弈论 Game Theory
- 地理/地理信息科学 Geography/Geographic Information Science
- 图论 Graph Theory
- 工业工程 Industrial Engineering
- 库存控制 Inventory control
- 数学建模 Mathematical Modeling
- 数学优化 Mathematical Optimization
- 概率和统计 Probability and statistics
- 排队论 Queueing theory
- 社交网络/交通预测模型 Social network/traffic prediction modeling
- 随机过程 Stochastic processes
- 供应链管理 Supply chain management
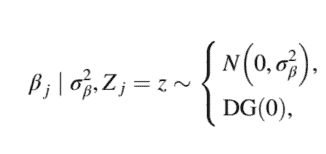
统计机器学习代写
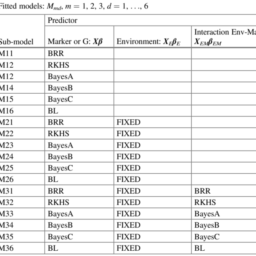
数学代写|统计机器学习作业代写Statistical Machine Learning代考|BayesC is the same as the BRR
For this model, the full conditional distributions of $\mu$ and $\sigma_{\beta}^{2}$ are the same as the model described before, that is, $\mu \mid-\sim N\left(\widetilde{\mu}, \tilde{\sigma}{\mu}^{2}\right)$ and $\sigma^{2} \mid-\sim \chi{\sim, s}^{-2}$. However, for the rest of the parameters, this does not have a known form and is not easy to simulate from them. A solution is to introduce a latent variable to represent the prior distribution of each $\beta_{j}$, and compute all the conditional distributions in this augmented scheme, including the distribution corresponding to the latent variable. To do this, note that this prior can be specified by assuming that conditional to a binary latent variable $Z_{j}$,
$$
\beta_{j} \mid \sigma_{\beta}^{2}, Z_{j}=z \sim\left{\begin{array}{l}
N\left(0, \sigma_{\beta}^{2}\right), \
\mathrm{DG}(0)
\end{array}\right.
$$
数学代写|统计机器学习作业代写STATISTICAL MACHINE LEARNING代考|Simulate from the full conditional
where $Z_{j}$ is a Bernoulli random variable with parameter $\pi_{p}\left(Z_{j} \sim \operatorname{Ber}\left(\pi_{p}\right)\right)$. With this introduced latent variable, all the full conditionals can be derived, as is described next.
If the current value of $z_{j}$ is 1 , the full conditional posterior of $\beta_{j}$ is
$$
\begin{aligned}
f\left(\beta_{j} \mid-\right) & \propto L\left(\mu, \boldsymbol{\beta}{0}, \sigma^{2} ; \boldsymbol{y}\right) f\left(\beta{j} \mid \sigma_{\beta}^{2}, z_{j}\right) \
& \propto \exp \left(-\frac{1}{2 \sigma^{2}}\left|\boldsymbol{y}-1_{n} \mu-\boldsymbol{X}{1} \boldsymbol{\beta}{0}\right|\right) \frac{1}{\sqrt{2 \pi \sigma_{\beta}^{2}}} \exp \left(-\frac{\beta_{j}^{2}}{2 \sigma_{\beta}^{2}}\right) \
& \propto \exp \left(-\frac{1}{2 \sigma^{2}} \sum_{i=1}^{n}\left(y_{i j}-x_{i j} \beta_{j}\right)^{2}-\frac{1}{2 \sigma_{\beta}^{2}} \beta_{j}^{2}\right) \
& \propto \exp \left{-\frac{1}{2}\left[\left(\sigma_{\beta}^{-2}+\sigma^{-2} \sum_{i=1}^{n} x_{i j}^{2}\right) \beta_{j}^{2}-2 \sigma^{-2} \sum_{i=1}^{n} x_{i j} y_{i j} \beta_{j}+\frac{1}{\sigma^{2}} \sum_{i=1}^{n} y_{i j}^{2}\right]\right} \
& \propto \exp \left[-\frac{\left.\left(\beta_{j}-\tilde{\beta}{j}\right)^{2}\right]}{2 \tilde{\sigma}{j}^{2}}\right],
\end{aligned}
$$
where $\quad y_{i j}=y_{i}-\sum_{k=1}^{p} x_{i k} \beta_{k} \quad, \quad \tilde{\sigma}{j}^{2}=\left(\sigma{\beta}^{-2}+\sigma^{-2} \sum_{i=1}^{n} x_{i j}^{2}\right)^{-1}, \quad$ and $\quad \tilde{\beta}{j}=$ $k \neq j$ $\sigma^{-2} \tilde{\sigma}{j}^{2} \sum_{i=1}^{n} x_{i j} y_{i j}$. That is, when the current value of $z_{j}$ is $1, \beta_{j} \mid-\sim N\left(\tilde{\beta}{j}, \tilde{\sigma}{j}^{2}\right)$. However, if $z_{j}=0$, the full conditional posterior of $\beta_{j}$ is a degenerate random variable at 0 , that is, $\beta_{j} \mid-\sim \mathrm{DG}(0)$.
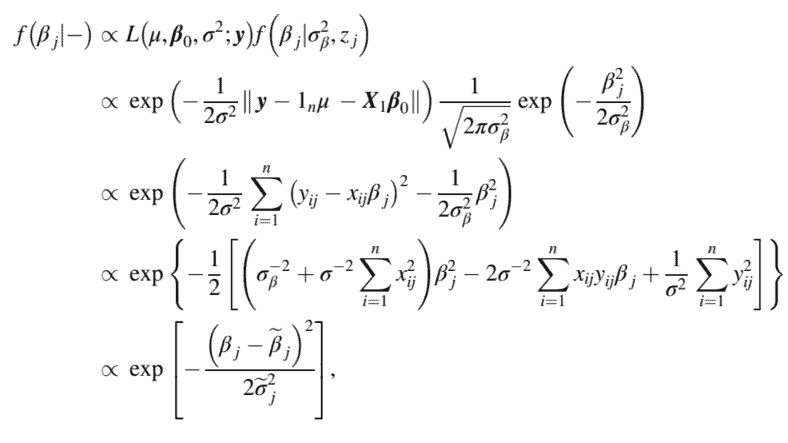
统计机器学习代考
数学代写|统计机器学习作业代写STATISTICAL MACHINE LEARNING代考|BAYESC IS THE SAME AS THE BRR
对于这个模型,完整的条件分布μ和σb2与之前描述的模型相同,即
$\mu$ and $\sigma_{\beta}^{2}$ are the same as the model described before, that is, $\mu \mid-\sim N\left(\widetilde{\mu}, \tilde{\sigma}{\mu}^{2}\right)$ and $\sigma^{2} \mid-\sim \chi{\tilde{v}, S}^{-2}$. However, for the rest of the parameters, this does not have a known form and is not easy to simulate from them. A solution is to introduce a latent variable to represent the prior distribution of each $\beta_{j}$, and compute all the conditional distributions in this augmented scheme, including the distribution corresponding to the latent variable. To do this, note that this prior can be specified by assuming that conditional to a binary latent variable $Z_{j}$,
$$
\beta_{j} \mid \sigma_{\beta}^{2}, Z_{j}=z \sim\left{\begin{array}{l}
N\left(0, \sigma_{\beta}^{2}\right) \
\mathrm{DG}(0)
\end{array}\right.
$$
where $Z_{j}$ is a Bernoulli random variable with parameter $\pi_{p}\left(Z_{j} \sim \operatorname{Ber}\left(\pi_{p}\right)\right)$.
正确的。
数学代写|统计机器学习作业代写STATISTICAL MACHINE LEARNING代考|SIMULATE FROM THE FULL CONDITIONAL
在哪里和j是带参数的伯努利随机变量圆周率p(和j∼贝尔(圆周率p)). 使用这个引入的潜在变量,可以导出所有完整的条件,如下所述。
如果当前值为和j是 1 ,完全条件后验bj是
$$
\begin{aligned}
f\left(\beta_{j} \mid-\right) & \propto L\left(\mu, \boldsymbol{\beta}{0}, \sigma^{2} ; \boldsymbol{y}\right) f\left(\beta{j} \mid \sigma_{\beta}^{2}, z_{j}\right) \
& \propto \exp \left(-\frac{1}{2 \sigma^{2}}\left|\boldsymbol{y}-1_{n} \mu-\boldsymbol{X}{1} \boldsymbol{\beta}{0}\right|\right) \frac{1}{\sqrt{2 \pi \sigma_{\beta}^{2}}} \exp \left(-\frac{\beta_{j}^{2}}{2 \sigma_{\beta}^{2}}\right) \
& \propto \exp \left(-\frac{1}{2 \sigma^{2}} \sum_{i=1}^{n}\left(y_{i j}-x_{i j} \beta_{j}\right)^{2}-\frac{1}{2 \sigma_{\beta}^{2}} \beta_{j}^{2}\right) \
& \propto \exp \left{-\frac{1}{2}\left[\left(\sigma_{\beta}^{-2}+\sigma^{-2} \sum_{i=1}^{n} x_{i j}^{2}\right) \beta_{j}^{2}-2 \sigma^{-2} \sum_{i=1}^{n} x_{i j} y_{i j} \beta_{j}+\frac{1}{\sigma^{2}} \sum_{i=1}^{n} y_{i j}^{2}\right]\right} \
& \propto \exp \left[-\frac{\left.\left(\beta_{j}-\tilde{\beta}{j}\right)^{2}\right]}{2 \tilde{\sigma}{j}^{2}}\right]
\end{aligned}
$$
where $\quad y_{i j}=y_{i}-\sum_{k=1}^{p} x_{i k} \beta_{k} \quad, \quad \widetilde{\sigma}{j}^{2}=\left(\sigma{\beta}^{-2}+\sigma^{-2} \sum_{i=1}^{n} x_{i j}^{2}\right)^{-1} \quad, \quad$ and $\quad \widetilde{\beta}{j}=$ $k \neq j$ $\sigma^{-2} \tilde{\sigma}{j}^{2} \sum_{i=1}^{n} x_{i j} y_{i j}$. That is, when the current value of $z_{j}$ is $1, \beta_{j} \mid-\sim N\left(\tilde{\beta}{j}, \tilde{\sigma}{j}^{2}\right)$. However, if $z_{j}=0$, the full conditional posterior of $\beta_{j}$ is a degenerate random variable at 0 , that is, $\beta_{j} \mid-\sim \mathrm{DG}(0)$.
The full conditional distribution of $Z_{j}$ is

随机过程代考
在概率论概念中,随机过程是随机变量的集合。 若一随机系统的样本点是随机函数,则称此函数为样本函数,这一随机系统全部样本函数的集合是一个随机过程。 实际应用中,样本函数的一般定义在时间域或者空间域。 随机过程的实例如股票和汇率的波动、语音信号、视频信号、体温的变化,随机运动如布朗运动、随机徘徊等等。
贝叶斯方法代考
贝叶斯统计概念及数据分析表示使用概率陈述回答有关未知参数的研究问题以及统计范式。后验分布包括关于参数的先验分布,和基于观测数据提供关于参数的信息似然模型。根据选择的先验分布和似然模型,后验分布可以解析或近似,例如,马尔科夫链蒙特卡罗 (MCMC) 方法之一。贝叶斯统计概念及数据分析使用后验分布来形成模型参数的各种摘要,包括点估计,如后验平均值、中位数、百分位数和称为可信区间的区间估计。此外,所有关于模型参数的统计检验都可以表示为基于估计后验分布的概率报表。
广义线性模型代考
广义线性模型(GLM)归属统计学领域,是一种应用灵活的线性回归模型。该模型允许因变量的偏差分布有除了正态分布之外的其它分布。
statistics-lab作为专业的留学生服务机构,多年来已为美国、英国、加拿大、澳洲等留学热门地的学生提供专业的学术服务,包括但不限于Essay代写,Assignment代写,Dissertation代写,Report代写,小组作业代写,Proposal代写,Paper代写,Presentation代写,计算机作业代写,论文修改和润色,网课代做,exam代考等等。写作范围涵盖高中,本科,研究生等海外留学全阶段,辐射金融,经济学,会计学,审计学,管理学等全球99%专业科目。写作团队既有专业英语母语作者,也有海外名校硕博留学生,每位写作老师都拥有过硬的语言能力,专业的学科背景和学术写作经验。我们承诺100%原创,100%专业,100%准时,100%满意。
机器学习代写
随着AI的大潮到来,Machine Learning逐渐成为一个新的学习热点。同时与传统CS相比,Machine Learning在其他领域也有着广泛的应用,因此这门学科成为不仅折磨CS专业同学的“小恶魔”,也是折磨生物、化学、统计等其他学科留学生的“大魔王”。学习Machine learning的一大绊脚石在于使用语言众多,跨学科范围广,所以学习起来尤其困难。但是不管你在学习Machine Learning时遇到任何难题,StudyGate专业导师团队都能为你轻松解决。
多元统计分析代考
基础数据: N 个样本, P 个变量数的单样本,组成的横列的数据表
变量定性: 分类和顺序;变量定量:数值
数学公式的角度分为: 因变量与自变量
时间序列分析代写
随机过程,是依赖于参数的一组随机变量的全体,参数通常是时间。 随机变量是随机现象的数量表现,其时间序列是一组按照时间发生先后顺序进行排列的数据点序列。通常一组时间序列的时间间隔为一恒定值(如1秒,5分钟,12小时,7天,1年),因此时间序列可以作为离散时间数据进行分析处理。研究时间序列数据的意义在于现实中,往往需要研究某个事物其随时间发展变化的规律。这就需要通过研究该事物过去发展的历史记录,以得到其自身发展的规律。
回归分析代写
多元回归分析渐进(Multiple Regression Analysis Asymptotics)属于计量经济学领域,主要是一种数学上的统计分析方法,可以分析复杂情况下各影响因素的数学关系,在自然科学、社会和经济学等多个领域内应用广泛。
MATLAB代写
MATLAB 是一种用于技术计算的高性能语言。它将计算、可视化和编程集成在一个易于使用的环境中,其中问题和解决方案以熟悉的数学符号表示。典型用途包括:数学和计算算法开发建模、仿真和原型制作数据分析、探索和可视化科学和工程图形应用程序开发,包括图形用户界面构建MATLAB 是一个交互式系统,其基本数据元素是一个不需要维度的数组。这使您可以解决许多技术计算问题,尤其是那些具有矩阵和向量公式的问题,而只需用 C 或 Fortran 等标量非交互式语言编写程序所需的时间的一小部分。MATLAB 名称代表矩阵实验室。MATLAB 最初的编写目的是提供对由 LINPACK 和 EISPACK 项目开发的矩阵软件的轻松访问,这两个项目共同代表了矩阵计算软件的最新技术。MATLAB 经过多年的发展,得到了许多用户的投入。在大学环境中,它是数学、工程和科学入门和高级课程的标准教学工具。在工业领域,MATLAB 是高效研究、开发和分析的首选工具。MATLAB 具有一系列称为工具箱的特定于应用程序的解决方案。对于大多数 MATLAB 用户来说非常重要,工具箱允许您学习和应用专业技术。工具箱是 MATLAB 函数(M 文件)的综合集合,可扩展 MATLAB 环境以解决特定类别的问题。可用工具箱的领域包括信号处理、控制系统、神经网络、模糊逻辑、小波、仿真等。