如果你也在 怎样代写图像处理Image Processing这个学科遇到相关的难题,请随时右上角联系我们的24/7代写客服。图像处理mage Processing的许多技术,或通常称为数字图片处理,是在20世纪60年代,在贝尔实验室、喷气推进实验室、麻省理工学院、马里兰大学和其他一些研究机构开发的,应用于卫星图像、有线照片标准转换、医学成像、可视电话、字符识别和照片增强。
图像处理作业Image Processing是使用数字计算机通过算法处理数字图像。 作为数字信号处理的一个子类别或领域,数字图像处理比模拟图像处理有许多优势。它允许更广泛的算法应用于输入数据,并能避免处理过程中的噪音和失真堆积等问题。由于图像是在两个维度(也许更多)上定义的,所以数字图像处理可以以多维系统的形式进行建模。数字图像处理的产生和发展主要受三个因素的影响:第一,计算机的发展;第二,数学的发展(特别是离散数学理论的创立和完善);第三,环境、农业、军事、工业和医学等方面的广泛应用需求增加。
my-assignmentexpert™ 图像处理Image Processing作业代写,免费提交作业要求, 满意后付款,成绩80\%以下全额退款,安全省心无顾虑。专业硕 博写手团队,所有订单可靠准时,保证 100% 原创。my-assignmentexpert™, 最高质量的图像处理Image Processing作业代写,服务覆盖北美、欧洲、澳洲等 国家。 在代写价格方面,考虑到同学们的经济条件,在保障代写质量的前提下,我们为客户提供最合理的价格。 由于统计Statistics作业种类很多,同时其中的大部分作业在字数上都没有具体要求,因此图像处理Image Processing作业代写的价格不固定。通常在经济学专家查看完作业要求之后会给出报价。作业难度和截止日期对价格也有很大的影响。
想知道您作业确定的价格吗? 免费下单以相关学科的专家能了解具体的要求之后在1-3个小时就提出价格。专家的 报价比上列的价格能便宜好几倍。
my-assignmentexpert™ 为您的留学生涯保驾护航 在数学mathematics作业代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的图像处理Image Processing作业代写代写服务。我们的专家在数学mathematics代写方面经验极为丰富,各种图像处理Image Processing相关的作业也就用不着 说。
我们提供的图像处理Image Processing及其相关学科的代写,服务范围广, 其中包括但不限于:
数学代写|图像处理作业代写Image Processing代考|Stochastic Processes
A stochastic process, $X_{t}$, is defined as
$$
X_{\mathrm{t}} \equiv X(t, \omega)
$$
where
$X_{t}=$ the value of a random variable $X$ at time $t$, for some value of $\omega$;
$t=$ time, either discrete or continuous; and
$\omega=$ a random element from a sample space $\Omega$.
If $t$ is fixed, say $t=t_{0}$, then we have a random variable over the sample space. For example, if $\Omega$ is a population of people, $X_{t_{0}}$ are the values of variable $X$ for all of the individuals in the population at the moment $t=t_{0}$. If $\omega$ is fixed, say $\omega=\omega_{0}$, then we have a sample trajectory over time for individual $\omega_{0}$.
Time series data consists of a series of real numbers. However, all real numbers can be cast in the imaginary plane. In addition to its standard form (i.e., $a+b i$ ), a complex number can be placed in either polar form or exponential form, both of which have distinct advantages.
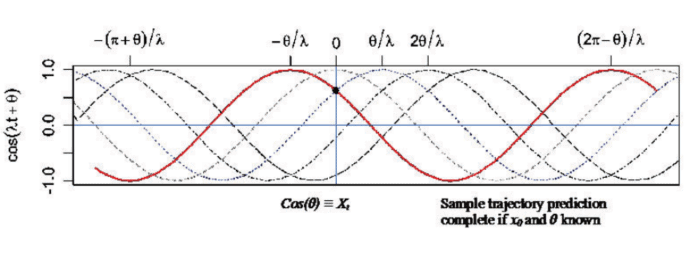
Setting $a=X \operatorname{Cos} \lambda t$ and $b=X \operatorname{Sin} \lambda t$, we have $a+b i=(X \operatorname{Cos} \lambda t)+$ $(X \operatorname{Sin} \lambda t) i$, where $X$ is the amplitude, $\lambda$ is the frequency, and $t$ is the time. The chief advantage with polar form is that it captures periodicity in time series data because of its use of the sine and cosine functions. By virtue of Euler’s formula, the polar form can be recast in exponential form as $X e^{i \lambda t}=(X \operatorname{Cos} \lambda t)+(X \operatorname{Sin} \lambda t) i$. The chief advantage of the exponential form is its greater facility in manipulating formulas within derivations and proofs. Both polar and exponential forms are used throughout the following discussion, with the particular form dependent on whichever has the greatest advantage in a particular context.
数学代写|图像处理作业代写Image Processing代考|Aliasing Effect
Whenever two time series are indistinguishable, there is said to be a possible aliasing effect. If time is discrete, with $t=\ldots-2,-1,0,1,2, \ldots$, the time series in Example 3 for $\lambda_{2}$ and $\lambda_{1}$ are indistinguishable if $\lambda_{2}=\lambda_{1}+2 \pi k$, where $k$ is some integer. In general, $X_{t}=X e^{i \lambda t}$ with amplitude $X$. If $X_{t}=$ $X e^{i \lambda_{2} t}$, by substitution we have
$$
\begin{aligned}
&X_{t}=X e^{i \lambda_{2} t} \
&=e^{i\left(\lambda_{1}+2 \pi k\right) t} \
&=e^{i \lambda_{1} t} e^{i 2 \pi(k t)} \
&=e^{i \lambda_{1} t} \cdot 1 \
&=e^{i \lambda_{1} t}
\end{aligned}
$$
In general, if $t=k \cdot \Delta t$, with $k$ an integer, then for $\lambda_{1}, \lambda_{2}$
$$
\left|\lambda_{1}-\lambda_{2}\right|=\frac{2 \pi}{\Delta t} \cdot m
$$
and there is an aliasing effect; thus, the time series is indistinguishable because
$$
X e^{i \lambda_{1} t}=X e^{i \lambda_{2} t}
$$
for $t=k \cdot \Delta t$. Consequently, observation of a discrete time series does not distinguish two alias frequencies.
数学代写|图像处理作业代写IMAGE PROCESSING代考|Spectral Representation
Any time series that is stationary in a wide sense can be represented as
$$
X_{t}=\int_{-\pi}^{\pi} e^{i \lambda t} a(\lambda) d \lambda
$$
where
$X_{t}=$ the value of variable $X$ at time $t$;
$e^{i \lambda t}=\operatorname{Cos}(\lambda t)+i \operatorname{Sin}(\lambda t)$, with frequency $\lambda$; and
$a(\lambda)=$ random amplitude of the time series.
with $\operatorname{Cov}\left(a\left(\lambda_{1}\right), a\left(\lambda_{2}\right)\right)=0$, where $\lambda_{1} \neq \lambda_{2}$. Because $X_{t}$ is a real number, $a(\lambda)=\frac{(a(-\lambda)}{a}$.
The spectral density, $f(\lambda)$, is
$$
f(\lambda)=E\left(|a(\lambda)|^{2}\right.
$$
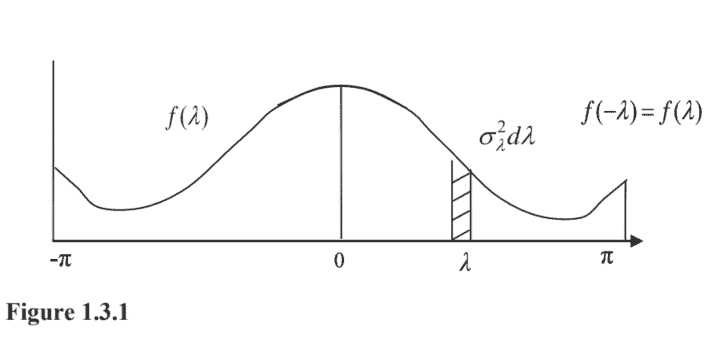
In other words, the spectral density is the variance of the amplitude, $a(\lambda)$, over a given range of frequencies. Further, for $E\left(X_{t}\right)=0$, the variance of $X_{t}$ is
$$
\operatorname{Var} X_{t} \stackrel{\text { for } E X_{t}=0}{=} E X_{t} \bar{X}{t}=\int{-\pi}^{\pi} f(\lambda) d \lambda
$$
(see Figure 1.3.1).
图像处理代写
数学代写|图像处理作业代写IMAGE PROCESSING代考|STOCHASTIC PROCESSES
一个随机过程,X吨, 定义为
X吨≡X(吨,ω)
在哪里
X吨=随机变量的值X有时吨, 对于某个值ω;
吨=时间,离散的或连续的;和
ω=来自样本空间的随机元素Ω.
如果吨是固定的,比如说吨=吨0,那么我们在样本空间上有一个随机变量。例如,如果Ω是一群人,X吨0是变量的值X对于目前人口中的所有个人吨=吨0. 如果ω是固定的,比如说ω=ω0,那么我们有一个样本轨迹随时间变化ω0.
时间序列数据由一系列实数组成。但是,所有实数都可以投射在虚平面上。除了它的标准形式一世.和.,$一种+b一世$, 一个复数可以用极坐标形式或指数形式表示,这两种形式都有明显的优势。
环境一种=X某物λ吨和b=X没有λ吨, 我们有一种+b一世=(X某物λ吨)+ (X没有λ吨)一世, 在哪里X是幅度,λ是频率,并且吨是时候了。极坐标形式的主要优点是它可以捕获时间序列数据中的周期性,因为它使用了正弦和余弦函数。借助欧拉公式,极坐标形式可以重铸为指数形式X和一世λ吨=(X某物λ吨)+(X没有λ吨)一世. 指数形式的主要优点是它在推导和证明中更容易操作公式。极坐标和指数形式都在以下讨论中使用,具体形式取决于在特定上下文中具有最大优势的形式。
数学代写|图像处理作业代写IMAGE PROCESSING代考|ALIASING EFFECT
每当两个时间序列无法区分时,就可以说可能存在混叠效应。如果时间是离散的,则吨=…−2,−1,0,1,2,…,示例 3 中的时间序列为λ2和λ1无法区分,如果λ2=λ1+2圆周率到, 在哪里到是某个整数。一般来说,X吨=X和一世λ吨有振幅X. 如果X吨= X和一世λ2吨, 通过替换我们有
X吨=X和一世λ2吨 =和一世(λ1+2圆周率到)吨 =和一世λ1吨和一世2圆周率(到吨) =和一世λ1吨⋅1 =和一世λ1吨
一般来说,如果吨=到⋅Δ吨, 和到一个整数,那么对于λ1,λ2
|λ1−λ2|=2圆周率Δ吨⋅米
并且有混叠效应;因此,时间序列是无法区分的,因为
X和一世λ1吨=X和一世λ2吨
为了吨=到⋅Δ吨. 因此,离散时间序列的观察不能区分两个混叠频率。
数学代写|图像处理作业代写IMAGE PROCESSING代考|SPECTRAL REPRESENTATION
任何广义上静止的时间序列都可以表示为
X吨=∫−圆周率圆周率和一世λ吨一种(λ)dλ
在哪里
X吨=变量的值X有时吨;
和一世λ吨=某物(λ吨)+一世没有(λ吨), 频率λ; 和
一种(λ)=时间序列的随机幅度。
和这(一种(λ1),一种(λ2))=0, 在哪里λ1≠λ2. 因为X吨是一个实数,一种(λ)=(一种(−λ)一种.
光谱密度,F(λ), 是
F(λ)=和(|一种(λ)|2
换句话说,频谱密度是幅度的方差,一种(λ),在给定的频率范围内。此外,对于和(X吨)=0, 的方差X吨是
$$
\operatorname{Var} X_{t} \stackrel{\text { for } E X_{t}=0}{=} E X_{t} \bar{X} {t}=\int {-\ pi}^{\pi} fλd \lambda
$$
s和和F一世G你r和1.3.1.

matlab代写请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。