如果你也在 怎样代写计算金融Computational finance这个学科遇到相关的难题,请随时右上角联系我们的24/7代写客服。计算金融Computational finance是应用计算机科学的一个分支,处理金融中的实际利益问题。一些略有不同的定义是研究目前用于金融的数据和算法以及实现金融模型或系统的计算机程序的数学。
计算金融Computational finance强调实用的数字方法,而不是数学证明,并侧重于直接应用于经济分析的技术。它是数学金融学和数字方法之间的一个跨学科领域。两个主要领域是金融证券公允价值的有效和准确计算以及随机时间序列的建模。计算金融作为一门学科的诞生可以追溯到20世纪50年代初的哈里-马科维茨。马科维茨将投资组合的选择问题设想为均值-方差优化的一个练习。这需要比当时更多的计算机能力,所以他致力于研究有用的近似解决方案的算法。
my-assignmentexpert™ 计算金融Computational finance作业代写,免费提交作业要求, 满意后付款,成绩80\%以下全额退款,安全省心无顾虑。专业硕 博写手团队,所有订单可靠准时,保证 100% 原创。my-assignmentexpert™, 最高质量的计算金融Computational finance作业代写,服务覆盖北美、欧洲、澳洲等 国家。 在代写价格方面,考虑到同学们的经济条件,在保障代写质量的前提下,我们为客户提供最合理的价格。 由于统计Statistics作业种类很多,同时其中的大部分作业在字数上都没有具体要求,因此计算金融Computational finance作业代写的价格不固定。通常在经济学专家查看完作业要求之后会给出报价。作业难度和截止日期对价格也有很大的影响。
想知道您作业确定的价格吗? 免费下单以相关学科的专家能了解具体的要求之后在1-3个小时就提出价格。专家的 报价比上列的价格能便宜好几倍。
my-assignmentexpert™ 为您的留学生涯保驾护航 在计算金融project作业代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的计算金融project代写服务。我们的专家在计算金融Computational finance代写方面经验极为丰富,各种计算金融Computational finance相关的作业也就用不着 说。
我们提供的计算金融Computational finance及其相关学科的代写,服务范围广, 其中包括但不限于:
金融代写|计算金融project代写Computational finance代考|Method of Lines
For the numerical solution of initial-boundary value problems for convection-diffusion-reaction equations (2.1) the method of lines (MOL) forms a flexible and versatile approach. It is widely employed in practice and is popular in particular in computational finance. The MOL consists of two general, consecutive steps:
(S) discretization in the space variable $s$,
(T) discretization in the time variable $t$.
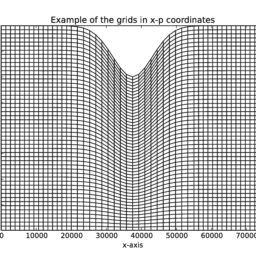
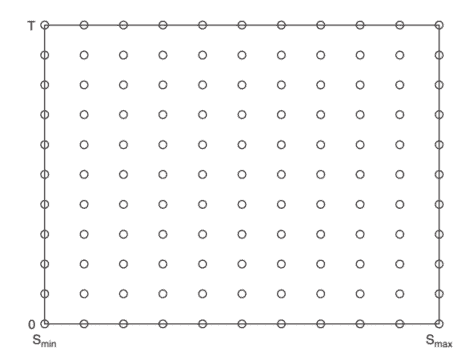
Step (S) is referred to as spatial discretization or semidiscretization. In this step the initial-boundary value problem for the PDE is discretized on a finite grid in the $s$-domain. This leads to an initial value problem for a (large) system of ODEs, the so-called semidiscrete system. Step (T) is referred to as temporal discretization. Here the semidiscrete system is discretized on a finite grid in the $t$-domain and defines the actual, fully discrete approximations on the obtained Cartesian grid in the $(s, t)$-domain. A sample $(s, t)$-grid is shown in Figure 3.1.
The present and the subsequent two chapters deal with step (S). We shall discuss several basic semidiscretizations of initial-boundary value problems for PDEs (2.1). In this chapter we commence with the model equation (2.3). Along with the initial condition (2.2), a so-called periodic (boundary) condition is taken here for simplicity,
$$
u(s+1, t)=u(s, t) \quad \text { for all } s \in \mathbb{R}, 0 \leq t \leq T .
$$
Thus the solution is assumed to be periodic in the spatial variable with period 1 . The model equation with periodic condition forms a natural starting point in the numerical literature as it enables a rigorous theoretical stability analysis that provides important practical insight. Notice that (3.1) is not a boundary condition in the strict sense, but it is still commonly named as such. Actual boundary conditions will be discussed in the next chapter.
In view of the periodicity, it suffices to consider semidiscretization on the spatial interval $(0,1]$. Let $m \geq 3$ be any given integer, let the spatial mesh width $h=1 / \mathrm{m}$ and let spatial grid points $s_{i}=i h$ for $i=0,1,2, \ldots, m$. The spatial discretizations under consideration in this book are based upon finite difference formulas. They yield approximations $U_{i}(t)$ to $u\left(s_{i}, t\right)$ for $1 \leq i \leq m, 0<t \leq T$. By the initial condition (2.2), the values at $t=0$ are directly known,
$$
U_{i}(0)=u_{0}\left(s_{i}\right) \quad \text { for } 1 \leq i \leq m
$$
金融代写|计算金融PROJECT代写COMPUTATIONAL FINANCE代考|Finite Difference Formulas
In the following we formulate several basic semidiscretizations for the model convection and diffusion equations separately. These are subsequently combined so as to arrive at semidiscretizations for the full model equation (2.3).
By classical real analysis, the first derivative $f^{\prime}$ of any given smooth function $f: \mathbb{R} \rightarrow \mathbb{R}$ at any point $s \in \mathbb{R}$ is approximated by
$$
f^{\prime}(s) \approx \frac{f(s)-f(s-h)}{h}
$$
whenever $h>0$ is small. The right-hand side of (3.3) is a finite difference quotient, involving two values of $f$. It is called the first-order backward formula. This formula can be interpreted as the slope of the line segment between the points $(s-h, f(s-h))$ and $(s, f(s))$ on the graph of $f$, see Figure 3.2.
Consider now the pure model convection equation $u_{t}(s, t)=c u_{s}(s, t)$ with periodic condition. Applying (3.3) to the spatial derivative term in this equation at grid point $s=s_{i}$, yields the approximate relation
$$
u_{t}\left(s_{i}, t\right) \approx c \frac{u\left(s_{i}, t\right)-u\left(s_{i-1}, t\right)}{h} \quad(1 \leq i \leq m, 0<t \leq T) .
$$
金融代写|计算金融PROJECT代写COMPUTATIONAL FINANCE代考|Stability
In this section we study the stability of the semidiscrete systems constructed in Section 3.2. All these systems are of the form (3.5). By virtue of the periodicity condition, all pertinent matrices $A$ are normal, that is, $A A^{\mathrm{T}}=A^{\mathrm{T}} A$. Consequently, for each matrix $A$, it holds that $A=V \Lambda V^{-1}$ with certain unitary matrix $V$ and diagonal matrix $\Lambda=\operatorname{diag}\left(\lambda_{1}, \lambda_{2}, \ldots, \lambda_{m}\right)$. The columns of $V$ are the eigenvectors of $A$ and the diagonal entries of $\Lambda$ are the eigenvalues of $A$.
Let $\mathbf{i}$ denote the imaginary unit. For the four matrices $A$ from Section $3.2$ explicit expressions for their eigenvalues $\lambda_{k}(1 \leq k \leq m)$ are known:
$$
\text { (3.6): } \lambda_{k}=\frac{c}{h}(1-\cos (2 \pi k h)+\mathbf{i} \sin (2 \pi k h)) \text {, }
$$
$$
\text { (3.9) }: \lambda_{k}=\frac{c}{h}(\cos (2 \pi k h)-1+\mathbf{i} \sin (2 \pi k h)) \text {, }
$$
(3.12): $\lambda_{k}=\mathbf{i} \frac{c}{h} \sin (2 \pi k h)$,
(3.15): $\lambda_{k}=-\frac{4 d}{h^{2}} \sin ^{2}(\pi k h)$.
Hence, for the first-order backward and forward formulas all eigenvalues lie on a circle in the complex plane with radius $\frac{|c|}{h}$ and midpoints $\left(\frac{c}{h}, 0\right)$ and $\left(-\frac{c}{h}, 0\right)$, respectively. For the second-order central formula for convection all eigenvalues lie on the imaginary axis, and for the second-order central formula for diffusion all eigenvalues lie on the negative real axis.
The stability analysis of semidiscrete systems deals with the propagation forward in time of perturbations in the initial vector. A given semidiscretization is said to be stable if the error incurred at any given time $t>0$ can be bounded by a moderate constant multiplied by the error at the initial time $t=0$, where the constant is independent of the spatial mesh width $h$ and the initial error.
To measure the sizes of vectors, consider the naturally scaled Euclidean norm
$$
|x|_{2}=\left{h \sum_{i=1}^{m}\left|x_{i}\right|^{2}\right}^{\frac{1}{2}} \text { whenever } x=\left(x_{1}, x_{2}, \ldots, x_{m}\right)^{\mathrm{T}} \in \mathbb{C}^{m}
$$

计算金融代写
金融代写|计算金融PROJECT代写COMPUTATIONAL FINANCE代考|METHOD OF LINES
对于对流-扩散-反应方程的初边值问题的数值解2.1线法米这大号形成一种灵活多变的方法。它在实践中得到广泛应用,尤其是在计算金融中很受欢迎。MOL 由两个一般的连续步骤组成:
小号空间变量中的离散化s,
吨时间变量的离散化吨.
步小号称为空间离散化或半离散化。在这一步中,PDE 的初始边界值问题在有限网格上离散化s-领域。这导致了一个初始值问题l一种rG和ODE 系统,即所谓的半离散系统。步吨称为时间离散化。这里半离散系统在有限网格上离散化吨-domain 并定义实际的、完全离散的近似值(s,吨)-领域。一个样品(s,吨)-grid 如图 3.1 所示。
本节及后续两章涉及步骤小号. 我们将讨论 PDE 初始边界值问题的几个基本半离散化2.1. 在本章中,我们从模型方程开始2.3. 连同初始条件2.2,所谓的周期性b这在nd一种r是为简单起见,此处采用条件,
在(s+1,吨)=在(s,吨) 对全部 s∈R,0≤吨≤吨.
因此,假设解在周期为 1 的空间变量中是周期性的。具有周期性条件的模型方程在数值文献中形成了一个自然的起点,因为它能够进行严格的理论稳定性分析,从而提供重要的实践见解。请注意3.1不是严格意义上的边界条件,但仍然通常如此命名。实际的边界条件将在下一章讨论。
鉴于周期性,在空间区间上考虑半离散化就足够了(0,1]. 让米≥3是任何给定的整数,让空间网格宽度H=1/米并让空间网格点s一世=一世H为了一世=0,1,2,…,米. 本书中考虑的空间离散化基于有限差分公式。它们产生近似值在一世(吨)到在(s一世,吨)为了1≤一世≤米,0<吨≤吨. 由初始条件2.2,值在吨=0是直接知道的,
在一世(0)=在0(s一世) 为了 1≤一世≤米
金融代写|计算金融PROJECT代写COMPUTATIONAL FINANCE代考|FINITE DIFFERENCE FORMULAS
下面我们分别为模型对流和扩散方程制定几个基本的半离散化。随后将这些组合起来,以得到完整模型方程的半离散化2.3.
通过经典实分析,一阶导数F′任何给定的平滑函数F:R→R在任何时候s∈R近似为
F′(s)≈F(s)−F(s−H)H
每当H>0是小。的右侧3.3是一个有限差分商,涉及两个值F. 它被称为一阶后向公式。这个公式可以解释为点之间线段的斜率(s−H,F(s−H))和(s,F(s))在图上F,见图 3.2。
现在考虑纯模型对流方程在吨(s,吨)=C在s(s,吨)具有周期性条件。申请3.3到该方程中网格点处的空间导数项s=s一世, 产生近似关系
在吨(s一世,吨)≈C在(s一世,吨)−在(s一世−1,吨)H(1≤一世≤米,0<吨≤吨).
金融代写|计算金融PROJECT代写COMPUTATIONAL FINANCE代考|STABILITY
在本节中,我们研究 3.2 节中构建的半离散系统的稳定性。所有这些系统都具有以下形式3.5. 由于周期性条件,所有相关的矩阵一种是正常的,也就是说,一种一种吨=一种吨一种. 因此,对于每个矩阵一种, 它认为一种=在Λ在−1具有一定的酉矩阵在和对角矩阵Λ=诊断(λ1,λ2,…,λ米). 的列在是的特征向量一种和对角线条目Λ是的特征值一种.
让一世表示虚数单位。对于四个矩阵一种从部分3.2其特征值的显式表达式λķ(1≤ķ≤米)已知:
(3.6): λķ=CH(1−因(2圆周率ķH)+一世罪(2圆周率ķH)),
(3.9) :λķ=CH(因(2圆周率ķH)−1+一世罪(2圆周率ķH)),
3.12: λķ=一世CH罪(2圆周率ķH),
3.15:λķ=−4dH2罪2(圆周率ķH).
因此,对于一阶后向和前向公式,所有特征值都位于具有半径的复平面中的圆上|C|H和中点(CH,0)和(−CH,0), 分别。对于对流的二阶中心公式,所有特征值都位于虚轴上,对于扩散的二阶中心公式,所有特征值都位于负实轴上。
半离散系统的稳定性分析处理初始向量中扰动的时间向前传播。如果在任何给定时间发生错误,则称给定半离散化是稳定的吨>0可以由一个适中的常数乘以初始时间的误差为界吨=0, 其中常数与空间网格宽度无关H和最初的错误。
要测量向量的大小,请考虑自然缩放的欧几里得范数
|x|_{2}=\left{h \sum_{i=1}^{m}\left|x_{i}\right|^{2}\right}^{\frac{1}{2} } \text { 每当 } x=\left(x_{1}, x_{2}, \ldots, x_{m}\right)^{\mathrm{T}} \in \mathbb{C}^{m}

金融代写|计算金融project代写Computational finance代考 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。
电磁学代考
物理代考服务:
物理Physics考试代考、留学生物理online exam代考、电磁学代考、热力学代考、相对论代考、电动力学代考、电磁学代考、分析力学代考、澳洲物理代考、北美物理考试代考、美国留学生物理final exam代考、加拿大物理midterm代考、澳洲物理online exam代考、英国物理online quiz代考等。
光学代考
光学(Optics),是物理学的分支,主要是研究光的现象、性质与应用,包括光与物质之间的相互作用、光学仪器的制作。光学通常研究红外线、紫外线及可见光的物理行为。因为光是电磁波,其它形式的电磁辐射,例如X射线、微波、电磁辐射及无线电波等等也具有类似光的特性。
大多数常见的光学现象都可以用经典电动力学理论来说明。但是,通常这全套理论很难实际应用,必需先假定简单模型。几何光学的模型最为容易使用。
相对论代考
上至高压线,下至发电机,只要用到电的地方就有相对论效应存在!相对论是关于时空和引力的理论,主要由爱因斯坦创立,相对论的提出给物理学带来了革命性的变化,被誉为现代物理性最伟大的基础理论。
流体力学代考
流体力学是力学的一个分支。 主要研究在各种力的作用下流体本身的状态,以及流体和固体壁面、流体和流体之间、流体与其他运动形态之间的相互作用的力学分支。
随机过程代写
随机过程,是依赖于参数的一组随机变量的全体,参数通常是时间。 随机变量是随机现象的数量表现,其取值随着偶然因素的影响而改变。 例如,某商店在从时间t0到时间tK这段时间内接待顾客的人数,就是依赖于时间t的一组随机变量,即随机过程
Matlab代写
MATLAB 是一种用于技术计算的高性能语言。它将计算、可视化和编程集成在一个易于使用的环境中,其中问题和解决方案以熟悉的数学符号表示。典型用途包括:数学和计算算法开发建模、仿真和原型制作数据分析、探索和可视化科学和工程图形应用程序开发,包括图形用户界面构建MATLAB 是一个交互式系统,其基本数据元素是一个不需要维度的数组。这使您可以解决许多技术计算问题,尤其是那些具有矩阵和向量公式的问题,而只需用 C 或 Fortran 等标量非交互式语言编写程序所需的时间的一小部分。MATLAB 名称代表矩阵实验室。MATLAB 最初的编写目的是提供对由 LINPACK 和 EISPACK 项目开发的矩阵软件的轻松访问,这两个项目共同代表了矩阵计算软件的最新技术。MATLAB 经过多年的发展,得到了许多用户的投入。在大学环境中,它是数学、工程和科学入门和高级课程的标准教学工具。在工业领域,MATLAB 是高效研究、开发和分析的首选工具。MATLAB 具有一系列称为工具箱的特定于应用程序的解决方案。对于大多数 MATLAB 用户来说非常重要,工具箱允许您学习和应用专业技术。工具箱是 MATLAB 函数(M 文件)的综合集合,可扩展 MATLAB 环境以解决特定类别的问题。可用工具箱的领域包括信号处理、控制系统、神经网络、模糊逻辑、小波、仿真等。