如果你也在 怎样代写计算金融Computational finance这个学科遇到相关的难题,请随时右上角联系我们的24/7代写客服。计算金融Computational finance是应用计算机科学的一个分支,处理金融中的实际利益问题。一些略有不同的定义是研究目前用于金融的数据和算法以及实现金融模型或系统的计算机程序的数学。
计算金融Computational finance强调实用的数字方法,而不是数学证明,并侧重于直接应用于经济分析的技术。它是数学金融学和数字方法之间的一个跨学科领域。两个主要领域是金融证券公允价值的有效和准确计算以及随机时间序列的建模。计算金融作为一门学科的诞生可以追溯到20世纪50年代初的哈里-马科维茨。马科维茨将投资组合的选择问题设想为均值-方差优化的一个练习。这需要比当时更多的计算机能力,所以他致力于研究有用的近似解决方案的算法。
my-assignmentexpert™ 计算金融Computational finance作业代写,免费提交作业要求, 满意后付款,成绩80\%以下全额退款,安全省心无顾虑。专业硕 博写手团队,所有订单可靠准时,保证 100% 原创。my-assignmentexpert™, 最高质量的计算金融Computational finance作业代写,服务覆盖北美、欧洲、澳洲等 国家。 在代写价格方面,考虑到同学们的经济条件,在保障代写质量的前提下,我们为客户提供最合理的价格。 由于统计Statistics作业种类很多,同时其中的大部分作业在字数上都没有具体要求,因此计算金融Computational finance作业代写的价格不固定。通常在经济学专家查看完作业要求之后会给出报价。作业难度和截止日期对价格也有很大的影响。
想知道您作业确定的价格吗? 免费下单以相关学科的专家能了解具体的要求之后在1-3个小时就提出价格。专家的 报价比上列的价格能便宜好几倍。
my-assignmentexpert™ 为您的留学生涯保驾护航 在计算金融project作业代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的计算金融project代写服务。我们的专家在计算金融Computational finance代写方面经验极为丰富,各种计算金融Computational finance相关的作业也就用不着 说。
我们提供的计算金融Computational finance及其相关学科的代写,服务范围广, 其中包括但不限于:
金融代写|计算金融project代写Computational finance代考|Convection-Diffusion-Reaction Equations
As opposed to ordinary differential equations (ODEs), partial differential equations (PDEs) concern functions of multiple independent variables. In this chapter we consider PDEs of the time-dependent convection-diffusion-reaction kind,
$$
\frac{\partial u}{\partial t}(s, t)=d(s) \frac{\partial^{2} u}{\partial s^{2}}(s, t)+c(s) \frac{\partial u}{\partial s}(s, t)-r(s) u(s, t)
$$
for $S_{\min }<s<S_{\max }$ and $0<t \leq T$. Here $S_{\min }, S_{\max }$ are given real values or $\pm \infty$ and $c, d, r$ denote given real-valued functions where $d$ is always assumed to be nonnegative. The real-valued function $u$ is the unknown.
Most of the PDEs that arise in contemporary financial option valuation theory are of the convection-diffusion-reaction kind. Clearly the choice
$$
c(s)=r s, d(s)=\frac{1}{2} \sigma^{2} s^{2}, r(s) \equiv r
$$
yields the Black-Scholes PDE (1.3). Further, one has $S_{\min }=0$ and $S_{\max }=\infty$ for standard call and put options.
In the literature, often an alternative notation by means of subscripts is used for the partial derivatives of a function. This gives a slightly
shorter formulation for (2.1), which we will often employ,
$$
u_{t}(s, t)=d(s) u_{s s}(s, t)+c(s) u_{s}(s, t)-r(s) u(s, t)
$$
金融代写|计算金融PROJECT代写COMPUTATIONAL FINANCE代考|The Model Equation
To gain first insight into possible solutions of convection-diffusionreaction equations, we let the spatial domain $\left(S_{\min }, S_{\max }\right)=\mathbb{R}$ and discuss the model equation,
$$
u_{t}(s, t)=d u_{s s}(s, t)+c u_{s}(s, t)-r u(s, t)
$$
with real constants $c, d, r$. We consider the convection, diffusion and reaction parts separately, starting with the simplest case.
Reaction equation The pure reaction equation $u_{t}(s, t)=-r u(s, t)$ is directly solved and yields the exact solution
$$
u(s, t)=e^{-r t} u_{0}(s) \quad \text { for } s \in \mathbb{R}, 0 \leq t \leq T .
$$
In a financial context, this represents discounting (with the risk-free rate).
Convection equation The pure convection equation $u_{t}(s, t)=c u_{s}(s, t)$ also has a simple exact solution, namely
$$
u(s, t)=u_{0}(s+c t) \quad \text { for } s \in \mathbb{R}, 0 \leq t \leq T .
$$
For any given fixed $t$, the graph of $u(\cdot, t)$ is a shift of the graph of the initial function $u_{0}$ with $-c t$ units. If $c>0$ then the shift is to the left, whereas if $c<0$ then it is to the right. When $s$ is interpreted as spatial position and $t$ as time, then $-c$ represents velocity.
金融代写|计算金融PROJECT代写COMPUTATIONAL FINANCE代考|Boundary Conditions
In computational practice, to render the numerical solution feasible, the spatial domain $\left(S_{\min }, S_{\max }\right)$ is taken as bounded and conditions on $u$ are prescribed at the boundary points of this domain.
For various financial options boundedness of the spatial domain intrinsically holds. For instance, it is often fulfilled for barrier options, which shall be discussed in Chapter 10. If the spatial domain is intrinsically unbounded, such as for standard call and put options, then it is common to truncate this domain.
Boundary conditions for PDEs appear in several types. The two best known are the Dirichlet boundary condition and the Neumann boundary condition. These conditions prescribe, respectively, the values of $u(s, t)$ and the values of the first-order derivative $u_{s}(s, t)$ at the pertinent spatial boundary.
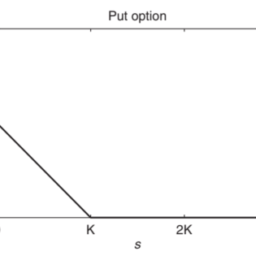
As an illustration, consider call and put options and a truncated domain $\left(0, S_{\max }\right)$. At the lower boundary $s=0$ the Dirichlet condition (1.5) applies. At the upper boundary $s=S_{\max }$ a common Dirichlet condition is specified by
$$
u\left(S_{\max }, t\right)=\left{\begin{array}{ll}
S_{\max }-e^{-r t} K & \text { for } 0 \leq t \leq T \quad \text { (call), } \
0 & \text { for } 0 \leq t \leq T
\end{array}\right. \text { (put) }
$$
and a Neumann condition by
$$
u_{s}\left(S_{\max }, t\right)=\left{\begin{array}{ll}
1 & \text { for } 0 \leq t \leq T \quad \text { (call) } \
0 & \text { for } 0 \leq t \leq T
\end{array} \quad\right. \text { (put) }
$$
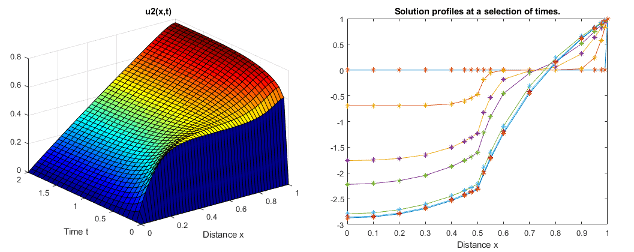
计算金融代写
金融代写|计算金融PROJECT代写COMPUTATIONAL FINANCE代考|CONVECTION-DIFFUSION-REACTION EQUATIONS
与常微分方程相反这D和s, 偏微分方程磷D和s关注多个自变量的函数。在本章中,我们考虑时间相关的对流-扩散-反应类型的偏微分方程,
∂在∂吨(s,吨)=d(s)∂2在∂s2(s,吨)+C(s)∂在∂s(s,吨)−r(s)在(s,吨)
为了小号分钟<s<小号最大限度和0<吨≤吨. 这里小号分钟,小号最大限度被赋予真实值或±∞和C,d,r表示给定的实值函数,其中d总是假定为非负的。实值函数在是未知数。
当代金融期权估值理论中出现的大多数偏微分方程都属于对流-扩散-反应类型。明确的选择
$$
c(s)=r s, d(s)=\frac{1}{2} \sigma^{2} s^{2}, r(s) \equiv r
$$
产生 Black-Scholes PDE1.3. 此外,一个有小号分钟=0和小号最大限度=∞用于标准看涨和看跌期权。
在文献中,通常使用下标的替代表示法来表示函数的偏导数。这给出了一个略
短的公式2.1,我们会经常使用,
$$
u_{t}(s, t)=d(s) u_{s s}(s, t)+c(s) u_{s}(s, t)-r(s) u(s, t)
$$
金融代写|计算金融PROJECT代写COMPUTATIONAL FINANCE代考|THE MODEL EQUATION
为了首先了解对流-扩散反应方程的可能解,我们让空间域(小号分钟,小号最大限度)=R并讨论模型方程,
在吨(s,吨)=d在ss(s,吨)+C在s(s,吨)−r在(s,吨)
有实常数C,d,r. 我们从最简单的情况开始分别考虑对流、扩散和反应部分。
反应方程式 纯反应方程式在吨(s,吨)=−r在(s,吨)直接求解并产生精确解
在(s,吨)=和−r吨在0(s) 为了 s∈R,0≤吨≤吨.
在金融环境中,这代表贴现在一世吨H吨H和r一世sķ−Fr和和r一种吨和.
对流方程 纯对流方程在吨(s,吨)=C在s(s,吨)也有一个简单的精确解,即
在(s,吨)=在0(s+C吨) 为了 s∈R,0≤吨≤吨.
对于任何给定的固定吨, 的图在(⋅,吨)是初始函数图的位移在0和−C吨单位。如果C>0那么移位是向左移动,而如果C<0然后它在右边。什么时候s被解释为空间位置和吨作为时间,那么−C表示速度。
金融代写|计算金融PROJECT代写COMPUTATIONAL FINANCE代考|BOUNDARY CONDITIONS
在计算实践中,为了使数值解可行,空间域(小号分钟,小号最大限度)被视为有界和条件在规定在该域的边界点。
对于各种金融期权,空间域的有界性本质上是成立的。例如,障碍期权经常实现,这将在第 10 章讨论。如果空间域本质上是无界的,例如标准看涨期权和看跌期权,那么通常截断这个域。
PDE 的边界条件有多种类型。最著名的两个是 Dirichlet 边界条件和 Neumann 边界条件。这些条件分别规定了在(s,吨)和一阶导数的值在s(s,吨)在相关的空间边界。
例如,考虑看涨期权和看跌期权以及截断域(0,小号最大限度). 在下边界s=0狄利克雷条件1.5适用。在上边界s=小号最大限度一个常见的狄利克雷条件由
$$
u\left(S_{\max }, t\right)=\left{\begin{array}{ll}
S_{\max }-e^{-r t} K & \text { for } 0 \leq t \leq T \quad \text { (call), } \
0 & \text { for } 0 \leq t \leq T
\end{array}\right. \text { (put) }
$$
and a Neumann condition by
$$
u_{s}\left(S_{\max }, t\right)=\left{\begin{array}{ll}
1 & \text { for } 0 \leq t \leq T \quad \text { (call) } \
0 & \text { for } 0 \leq t \leq T
\end{array} \quad\right. \text { (put) }
$$

金融代写|计算金融project代写Computational finance代考 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。
电磁学代考
物理代考服务:
物理Physics考试代考、留学生物理online exam代考、电磁学代考、热力学代考、相对论代考、电动力学代考、电磁学代考、分析力学代考、澳洲物理代考、北美物理考试代考、美国留学生物理final exam代考、加拿大物理midterm代考、澳洲物理online exam代考、英国物理online quiz代考等。
光学代考
光学(Optics),是物理学的分支,主要是研究光的现象、性质与应用,包括光与物质之间的相互作用、光学仪器的制作。光学通常研究红外线、紫外线及可见光的物理行为。因为光是电磁波,其它形式的电磁辐射,例如X射线、微波、电磁辐射及无线电波等等也具有类似光的特性。
大多数常见的光学现象都可以用经典电动力学理论来说明。但是,通常这全套理论很难实际应用,必需先假定简单模型。几何光学的模型最为容易使用。
相对论代考
上至高压线,下至发电机,只要用到电的地方就有相对论效应存在!相对论是关于时空和引力的理论,主要由爱因斯坦创立,相对论的提出给物理学带来了革命性的变化,被誉为现代物理性最伟大的基础理论。
流体力学代考
流体力学是力学的一个分支。 主要研究在各种力的作用下流体本身的状态,以及流体和固体壁面、流体和流体之间、流体与其他运动形态之间的相互作用的力学分支。
随机过程代写
随机过程,是依赖于参数的一组随机变量的全体,参数通常是时间。 随机变量是随机现象的数量表现,其取值随着偶然因素的影响而改变。 例如,某商店在从时间t0到时间tK这段时间内接待顾客的人数,就是依赖于时间t的一组随机变量,即随机过程
Matlab代写
MATLAB 是一种用于技术计算的高性能语言。它将计算、可视化和编程集成在一个易于使用的环境中,其中问题和解决方案以熟悉的数学符号表示。典型用途包括:数学和计算算法开发建模、仿真和原型制作数据分析、探索和可视化科学和工程图形应用程序开发,包括图形用户界面构建MATLAB 是一个交互式系统,其基本数据元素是一个不需要维度的数组。这使您可以解决许多技术计算问题,尤其是那些具有矩阵和向量公式的问题,而只需用 C 或 Fortran 等标量非交互式语言编写程序所需的时间的一小部分。MATLAB 名称代表矩阵实验室。MATLAB 最初的编写目的是提供对由 LINPACK 和 EISPACK 项目开发的矩阵软件的轻松访问,这两个项目共同代表了矩阵计算软件的最新技术。MATLAB 经过多年的发展,得到了许多用户的投入。在大学环境中,它是数学、工程和科学入门和高级课程的标准教学工具。在工业领域,MATLAB 是高效研究、开发和分析的首选工具。MATLAB 具有一系列称为工具箱的特定于应用程序的解决方案。对于大多数 MATLAB 用户来说非常重要,工具箱允许您学习和应用专业技术。工具箱是 MATLAB 函数(M 文件)的综合集合,可扩展 MATLAB 环境以解决特定类别的问题。可用工具箱的领域包括信号处理、控制系统、神经网络、模糊逻辑、小波、仿真等。