如果你也在 怎样代写概率论Probability Theory 这个学科遇到相关的难题，请随时右上角联系我们的24/7代写客服。概率论Probability Theory作为统计学的数学基础，对许多涉及数据定量分析的人类活动至关重要。概率论的方法也适用于对复杂系统的描述，只对其状态有部分了解，如在统计力学或顺序估计。二十世纪物理学的一个伟大发现是量子力学中描述的原子尺度的物理现象的概率性质。

概率论Probability Theory STAT131的核心课题包括离散和连续随机变量、概率分布和随机过程（为非决定性或不确定的过程或测量量提供数学抽象，这些过程或测量量可能是单一发生的，或以随机方式随时间演变）。尽管不可能完美地预测随机事件，但对它们的行为可以有很多说法。概率论中描述这种行为的两个主要结果是大数法则和中心极限定理。概率论是与概率有关的数学分支。虽然有几种不同的概率解释，但概率论以严格的数学方式处理这一概念，通过一组公理来表达它。

同学们在留学期间，都对各式各样的作业考试很是头疼，如果你无从下手，不如考虑my-assignmentexpert™！

my-assignmentexpert™提供最专业的一站式服务：Essay代写，Dissertation代写，Assignment代写，Paper代写，Proposal代写，Proposal代写，Literature Review代写，Online Course，Exam代考等等。my-assignmentexpert™专注为留学生提供Essay代写服务，拥有各个专业的博硕教师团队帮您代写，免费修改及辅导，保证成果完成的效率和质量。同时有多家检测平台帐号，包括Turnitin高级账户，检测论文不会留痕，写好后检测修改，放心可靠，经得起任何考验！

数学代写|概率论代考Probability Theory代写|From early beginnings to a model theory

The early history of probability was concerned primarily with the calculation of numerical probabilities for outcomes of games of chance. Perhaps the first book written along these lines was by the eccentric Gerolamo Cardano, a noted gambler, scholar, and bon vivant; his book Liber de Ludo Aleæ (Book on Games of Chance) was written perhaps in the 1560 s but only published posthumously in $1663 .{ }^1$ Numerical calculations continued to dominate over the next two and a half centuries awaiting the birth of a theory but the spread of applications continued unabated until, in the modern day, scarce an area of investigation is left untouched by probabilistic considerations.

Today the informed reader encounters probabilistic settings at every turn in divers applications. The following is a representative list of examples, in no particular order, that the reader will find familiar. (i) The conduct of opinion polls-and what the results say about the population as a whole. (ii) Sampling to determine the impact of an invasive species-or of pollutant concentrations. (iii) The prediction of user preferences-for movies or books or soap-from sporadic internet use. (iv) The search for order and predictability in the chaos of financial markets-or of sunspot activity. (v) Robot navigation over uncertain terrain. (vi) The analysis of noise in communications. (vii) The $3 \mathrm{~K}$ background cosmic radiation and what it portends for the universe. (viii) The statistical physics of radioactive decay. (ix) The description of flocking behaviour in wild geese and fish. (x) The analysis of risk in the design of actuarial tables. (xi) Mendel’s theory of heredity. (xii) Genetic combination and recombination, mutation. (xiii) The spread of infection. (xiv) Estimations of time to failure of machinery – or bridges or aeroplanes. (xv) Investment strategies and probabilities of ruin. (xvi) Queues – of telephone calls at an exchange, data packets at an internet server, or cars in a highway system. (xvii) The statistical search for the Higgs boson and other subatomic particles. The reader will be readily able to add to the list from her common experience.

Following the fumbling early beginnings, inevitably numerical, of investigations of the science of chance, as discoveries and applications gathered pace it became more and more necessary that the mathematical foundations of the subject be clearly articulated so that the numerical calculations, especially in areas that could not be readily tested, could be placed on firm mathematical ground. What should the goals of such a theory be? Given the vast realm of applicability we must hold fast against the temptation to hew the theory too close to any particular application. This is much as in how to reach its full flowering geometry had to be sundered from its physical roots. The rôle and importance of abstraction is in the extraction of the logical axiomatic content of the problem divorced of extraneous features that are not relevant, and indeed obfuscate, to provide a general-purpose tool that can be deployed to discover hitherto unsuspected patterns and new directions. Such a clean axiomatic programme was laid out by Andrei Kolmogorov in $1933 .

数学代写|概率论代考Probability Theory代写|Chance experiments

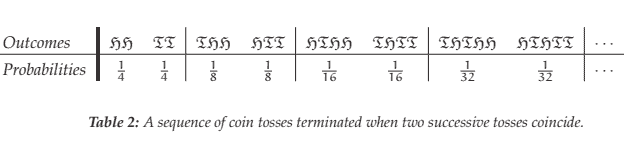
Our intuitive assignment of probabilities to results of chance experiments is based on an implicit mathematical idealisation of the notion of repeated independent trials. For instance, in a coin-tossing experiment, conditioned by a complex of experience and custom, we are inclined to treat the coin as “fair” and to ascribe probabilities of $1 / 2$ apiece for heads and tails ignoring possibilities such as that of the coin landing on edge or never coming down at all. Implicit here is the feeling that in a run of $n$ tosses all $2^n$ possible sequences of heads and tails are equally likely to occur. If in a long run of $n$ tosses there are $\mathrm{m}$ heads, we expect that the relative frequency $\mathrm{m} / \mathrm{n}$ of the occurrence of heads in the tosses will be very close to $1 / 2$, the accuracy getting better the larger $n$ is.
Now, to be sure, no coin is really “fair”. Statistical analyses of coin flips show invariably that heads and tails are not equally likely though the difference tends to be minute in most cases. Nonetheless, the mathematical fiction that a coin is fair is convenient in that it focuses on the essential features of the problem: it is not only simpler analytically but, for most applications, gives predictions that are sufficiently close to reality. We make similar assumptions about the throws of dice in the game of craps, the spin of a roulette wheel, or the distribution of bridge hands in cards. The following simple examples illustrate the key features of the modelling approach.

EXAMPLES: 1) $A$ coin is tossed three times. Representing heads by $\mathfrak{H}$ and tails by $\mathcal{T}$, the possible outcomes of the experiment may be tabulated in a natural convention as $\mathfrak{H} \mathfrak{H} \mathfrak{H}, \mathfrak{H} \mathfrak{H} T, \mathfrak{H} \mathfrak{T}, \mathfrak{H} \mathfrak{T}, \mathfrak{T} \mathfrak{H} \mathfrak{H}, \mathfrak{T} \mathfrak{H} \mathfrak{T}, \mathfrak{T} \mathfrak{H}$, and $\mathfrak{T T} \mathfrak{T}$. It is clear that these are the only possible outcomes of the idealised experiment and, abeyant any reason to think otherwise, we suppose that all outcomes have equal chance $1 / 8$ of occurrence. The event that exactly one head is seen may be identified with the aggregate of outcomes consisting of the sequences $\mathfrak{H T} \mathfrak{T}, \mathfrak{T H T}$, and $\mathfrak{T} \mathfrak{H}$ and it is natural to assign to this event the probability $3 / 8$.
2) The first throw in craps. A classical die consists of six faces which we may distinguish by inscribing the numbers 1 through 6 on them (or, as is more usual, by inscribing one through six dots on the faces). The dice game of craps begins by throwing two dice and summing their face values. If the sum of face values is equal to 2,3 , or 12 , the player loses immediately; if the sum is 7 or 11 , she wins immediately; otherwise, the game continues. What are the chances that a player at craps loses on the first throw? wins on the first throw?

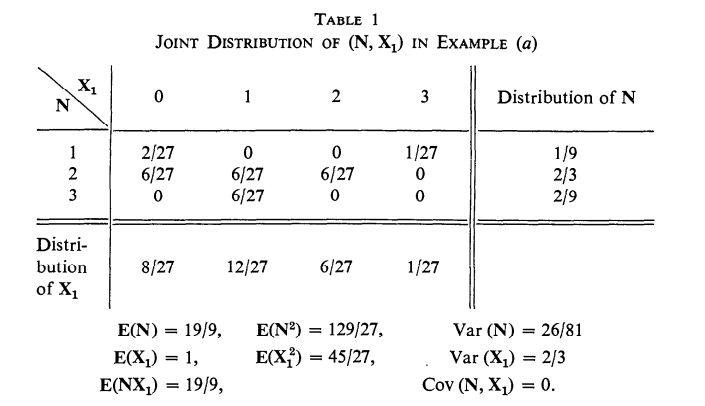
As the only element that decides the result of the first throw is the sum of face values it is natural to consider the outcomes of the experiment (as far as the first throw is concerned) to be the numbers 2 through 12. What are the chances we should ascribe to them? After a little thought the reader may come up with the numbers listed in Table 1. As a loss on the first throw is associated with the aggregate ${2,3,12}$, it is now reasonable to ascribe to it the probability $\frac{1}{36}+\frac{2}{36}+\frac{1}{36}=\frac{1}{9}$. Similarly, a win on the first throw has associated with it the aggregate of outcomes ${7,11}$ and accordingly has probability $\frac{6}{36}+\frac{2}{36}=\frac{2}{9}$. As any craps player knows, it is twice as likely that she wins on the first throw as that she loses on the first throw.

概率论代写

数学代写|概率论代考PROBABILITY THEORY代写|FROM EARLY BEGINNINGS TO A MODEL THEORY

概率的早期历史主要关注概率游戏结果的数值概率计算。也许按照这些思路写的第一本书是由古怪的杰罗拉莫·卡尔达诺 (Gerolamo Cardano) 写的，他是一位著名的 赌徒、学者和享乐主义者; 他的书 Liber de Ludo AleæBookonGamesofChance可能写于 1560 年代，但仅在死后发表于 1663 . ${ }^1$ 在接下来的两个半世纪里，数值计 算继续占据主导地位，等待理论的诞生，但应用的传播有增无减，直到现代，几乎没有一个研究领域末被概率考虑所触及。

今天，消息灵通的读者在各种应用程序中随时都会遇到概率设置。以下是具有代表性的示例列表（排名不分先后），读者会发现它们很孰悉。 $i$ 民意调查的进行-以及结果对整个人口的看法。 $i$ 取样以确定入侵物种或污染物浓度的影响。 $i i i$ 从零星的互联网使用中预测用户对电影、书籍或肥白剧的偏好。 $i v$ 在混乱的金融市场 或太阳黑子活动中寻找秩序和可预测性。v机器人在不确定地形上的导航。vi通信中的噪声分析。vii这 $3 \mathrm{~K}$ 背景宇宙辐射及其对宇宙的预示。viii放射性衰变的统 计物理学。 $i x$ 对大陮和鱼类群聚行为的描述。 $x$ 精算表设计中的风险分析。 $x i$ 孟德尔遗传学说。 $x i i$ 其因组合与重组、突变。 $x i i$ 感染的传播。 $x i v$ 估计机械故隌时 间 – 或桥梁或飞机。 $x v$ 投资策略和破产概率。 $x v i$ 队列—一交换机的电话呼叫、互联网服务器的数据包或高速公路系统中的汽车。xvi桸格斯玻色子和其他亚原子粒 子的统计搜索。读者可以很容易地从她的共同经验中添加到列表中。
随着机会科学的发现和应用的步伐加快，随着早期的摸索开始，不可避免地进行数值计算，越来越有必要清楚地阐明该学科的数学基础，以便进行数值计算，尤其是在可以计算的领域不容易测试，可以放在坚实的数学基础上。这种理论的目标应该是什么？鉴于广泛的适用范围，我们必须坚决抵制将理论过于接近任何特定应用的诱惑。这就像如何达到其完整的开花几何形状必须从其物理根部分离一样。抽象的作用和重要性在于提取问题的逻辑公理内容，与不相关的外来特征分离，并且确实混淆，以提供一个通用工具，可以部署它来发现迄今为止未被怀疑的模式和新方向。Andrei Kolmogorov 在 1933 年提出了这样一个干净的公理化程序。

数学代写|概率论代考PROBABILITY THEORY代写|CHANCE EXPERIMENTS

我们对机会实验结果的概率的直观分配是基于对重复独立试验概念的隐含数学理想化。例如，在以复杂的经验和习惯为条件的抛硬币实捡中，我们倾向于将硬币视 为“公平的”并将概率归因于 $1 / 2$ 每个正面和反面忽略可能性，例如硬市落在边幏或根本不掉下来的可能性。这里隐含的是一种感觉，在运行中 $n$ 扔所有 $2^n$ 正面和反 面的可能序列出现的可能性相同。如果在长期 $n$ 扔有 $m$ 头，我们期望相对频率 $m / n / \mathrm{n}$ 抛扶中正面朝上的概率将非常接近 $1 / 2$,精度越大越好 $n$ 是。
现在，可以肯定的是，没有硬币是真正“公平”的。抛硬币的统计分析总是表明，正面和反面出现的可能性并不相同，尽管在大多数棈况下差异往往很小。尽管如 此，硬币是公平的数学虚构是方便的，因为它关注问题的甚本特征：它不仅在分析上更简单，而且对于大多数应用来说，给出的预测非常接近现实。我们对扶骰子 游戏中的骰子、轮盘赌的旋转或纸牌中桥牌的分布做出类似的假设。以下简单示例说明了建模方法的主要特征。

示例: 1)A硬币被抛了三次。代表团长 $\mathfrak{H}$ 和尾巴 $\mathcal{T}$, 实验的可能结果可以按照自然惯例列为 $\mathfrak{H} \mathfrak{H} \mathfrak{H}, \mathfrak{H} \mathfrak{H} T, \mathfrak{H T}, \mathfrak{H T}, \mathfrak{T} \mathfrak{H}, \mathfrak{H} \mathfrak{H} \mathfrak{T}, \mathfrak{T} \mathfrak{H}$ ，和 $\mathfrak{T} \mathfrak{T}$. 很明显，这些是理想化 实验的唯一可能结果，并且除了任何其他想法之外，我们假设所有结果的机会均等 $1 / 8$ 的发生。恰好看到一个头的事件可以用由序列组成的结果集合来识别 $\mathfrak{H T T}, \mathfrak{H} \mathfrak{T} ，$ 和Th很自然地给这个事件分配概率 $3 / 8$.
2) 第一次郑殿子。经典埇子由六个面组成，我们可以通过在上面刻上数字 1 到 6 来区分它们or, asismoreusual, byinscribingonethroughsixdotsonthefaces. 㚘骰子的骰子游戏首先抛出两个骰子并将它们的面值相加。如果面值之和等于 2,3 或 12 ，则玩家立即输; 如果总和是 7 或 11 ，她立即获胜；否则，游戏继续。掷 骰子的玩家在第一次掷㬴子时输掉的几率是多少? 第一次投球就赢了?
由于决定第一次投扶结果的唯一因素是面值之和，因此自然要考虑实验结果asfarasthe firstthrowisconcerned是数字 2 到 12。我们应该购予它们多少机会? 稍 加思考后，读者可能会得出表 1 中列出的数字。 $2,3,12$, 现在可以合理地将概率归因于它 $\frac{1}{36}+\frac{2}{36}+\frac{1}{36}=\frac{1}{9}$. 同样，第一次投掷的胜利与结果的总和相关联 7,11 因 此有概率 $\frac{6}{36}+\frac{2}{36}=\frac{2}{9}$. 任何㚘骰子的玩家都知道，第一次扶筋子获胜的可能性是第一次䣠骰子失败的概率的两倍。

数学代写|概率论代考Probability Theory代写 请认准exambang™. exambang™为您的留学生涯保驾护航。

微观经济学代写

微观经济学是主流经济学的一个分支，研究个人和企业在做出有关稀缺资源分配的决策时的行为以及这些个人和企业之间的相互作用。my-assignmentexpert™ 为您的留学生涯保驾护航 在数学Mathematics作业代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的数学Mathematics代写服务。我们的专家在图论代写Graph Theory代写方面经验极为丰富，各种图论代写Graph Theory相关的作业也就用不着 说。

线性代数代写

线性代数是数学的一个分支，涉及线性方程，如：线性图，如：以及它们在向量空间和通过矩阵的表示。线性代数是几乎所有数学领域的核心。

博弈论代写

现代博弈论始于约翰-冯-诺伊曼（John von Neumann）提出的两人零和博弈中的混合策略均衡的观点及其证明。冯-诺依曼的原始证明使用了关于连续映射到紧凑凸集的布劳威尔定点定理，这成为博弈论和数学经济学的标准方法。在他的论文之后，1944年，他与奥斯卡-莫根斯特恩（Oskar Morgenstern）共同撰写了《游戏和经济行为理论》一书，该书考虑了几个参与者的合作游戏。这本书的第二版提供了预期效用的公理理论，使数理统计学家和经济学家能够处理不确定性下的决策。

微积分代写

微积分，最初被称为无穷小微积分或 “无穷小的微积分”，是对连续变化的数学研究，就像几何学是对形状的研究，而代数是对算术运算的概括研究一样。

它有两个主要分支，微分和积分；微分涉及瞬时变化率和曲线的斜率，而积分涉及数量的累积，以及曲线下或曲线之间的面积。这两个分支通过微积分的基本定理相互联系，它们利用了无限序列和无限级数收敛到一个明确定义的极限的基本概念 。

计量经济学代写

什么是计量经济学？
计量经济学是统计学和数学模型的定量应用，使用数据来发展理论或测试经济学中的现有假设，并根据历史数据预测未来趋势。它对现实世界的数据进行统计试验，然后将结果与被测试的理论进行比较和对比。

根据你是对测试现有理论感兴趣，还是对利用现有数据在这些观察的基础上提出新的假设感兴趣，计量经济学可以细分为两大类：理论和应用。那些经常从事这种实践的人通常被称为计量经济学家。

Matlab代写

MATLAB 是一种用于技术计算的高性能语言。它将计算、可视化和编程集成在一个易于使用的环境中，其中问题和解决方案以熟悉的数学符号表示。典型用途包括：数学和计算算法开发建模、仿真和原型制作数据分析、探索和可视化科学和工程图形应用程序开发，包括图形用户界面构建MATLAB 是一个交互式系统，其基本数据元素是一个不需要维度的数组。这使您可以解决许多技术计算问题，尤其是那些具有矩阵和向量公式的问题，而只需用 C 或 Fortran 等标量非交互式语言编写程序所需的时间的一小部分。MATLAB 名称代表矩阵实验室。MATLAB 最初的编写目的是提供对由 LINPACK 和 EISPACK 项目开发的矩阵软件的轻松访问，这两个项目共同代表了矩阵计算软件的最新技术。MATLAB 经过多年的发展，得到了许多用户的投入。在大学环境中，它是数学、工程和科学入门和高级课程的标准教学工具。在工业领域，MATLAB 是高效研究、开发和分析的首选工具。MATLAB 具有一系列称为工具箱的特定于应用程序的解决方案。对于大多数 MATLAB 用户来说非常重要，工具箱允许您学习和应用专业技术。工具箱是 MATLAB 函数（M 文件）的综合集合，可扩展 MATLAB 环境以解决特定类别的问题。可用工具箱的领域包括信号处理、控制系统、神经网络、模糊逻辑、小波、仿真等。