如果你也在 怎样代写微观经济学Microeconomics 这个学科遇到相关的难题，请随时右上角联系我们的24/7代写客服。微观经济学Microeconomics是主流经济学的一个分支，研究个人和公司在做出有关稀缺资源分配的决策时的行为以及这些个人和公司之间的互动。微观经济学侧重于研究单个市场、部门或行业，而不是宏观经济学所研究的整个国民经济。

微观经济学Microeconomic的一个目标是分析在商品和服务之间建立相对价格的市场机制，并在各种用途之间分配有限资源。微观经济学显示了自由市场导致理想分配的条件。它还分析了市场失灵，即市场未能产生有效的结果。微观经济学关注公司和个人，而宏观经济学则关注经济活动的总和，处理增长、通货膨胀和失业问题以及与这些问题有关的国家政策。微观经济学还处理经济政策（如改变税收水平）对微观经济行为的影响，从而对经济的上述方面产生影响。

同学们在留学期间，都对各式各样的作业考试很是头疼，如果你无从下手，不如考虑my-assignmentexpert™！

my-assignmentexpert™提供最专业的一站式服务：Essay代写，Dissertation代写，Assignment代写，Paper代写，Proposal代写，Proposal代写，Literature Review代写，Online Course，Exam代考等等。my-assignmentexpert™专注为留学生提供Essay代写服务，拥有各个专业的博硕教师团队帮您代写，免费修改及辅导，保证成果完成的效率和质量。同时有多家检测平台帐号，包括Turnitin高级账户，检测论文不会留痕，写好后检测修改，放心可靠，经得起任何考验！

想知道您作业确定的价格吗? 免费下单以相关学科的专家能了解具体的要求之后在1-3个小时就提出价格。专家的 报价比上列的价格能便宜好几倍。

我们在经济Economy代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的经济Economy代写服务。我们的专家在微观经济学Microeconomics代写方面经验极为丰富，各种微观经济学Microeconomics相关的作业也就用不着 说。

经济代写|微观经济学代考Microeconomics代写|Some models

Technically, an “evolutionist game” is defined by a stage game and a dynamic process. The stage game is stated in normal or extensive form, and only defines the utilities associated with the possible combinations of actions. The dynamic process specifies the principles of confrontation, information, evaluation and decision which are at work in the repetition of the stage game. It is thus by specifying the dynamics that the modeler can introduce the actual processes she thinks are pertinent, dealing with best responses, learning, selection, imitation, reinforcement, and so on.

Two kinds of contributions characterize evolutionist game theory. On one hand, the theory tried to find descriptions of the temporal behavior of the system that do not depend too much upon the detail of the considered dynamic process. Such results have been obtained for some classes of “simple” dynamic processes that only incorporate a selection or a reinforcement mechanism, coupled with a mutation or exploration mechanism of low intensity. On the other hand, evolutionist game theory has been able to provide new insights on some specific questions like the diffusion of technologies or the genesis of institutions. Several monographs provide surveys of the technical achievements of evolutionist game theory, for instance Maynard Smith (1982), Weibull (1995), Skyrms (1996), Vega-Redondo (1996), Samuelson (1997), Young (1998) or Fudenberg and Levine (1998).

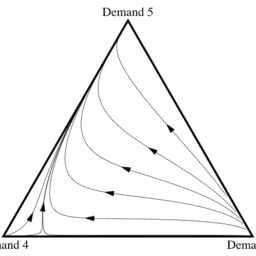
The models and interpretations of evolutionist game theory fluctuate between two poles: population dynamics and individual learning. In population dynamics, there is a large number of individuals, each of whom being endowed with a strategy he does not control. This strategy remains constant, except in case of mutations, which are random and relatively rare. Within one population, the variations of the proportion of users of a strategy are led by the selection process, which favors reproduction of the best fitted individuals. By contrast, the theory of individual learning makes the hypothesis that each individual can vary his strategy with time. This variation is stochastic when it incorporates a certain degree of active experimentation. If it is not supposed that the number of individuals is large, one nevertheless supposes that the individuals endlessly apply the same learning rules.

Not without generating some confusion, it is most remarkable that similar formal models appeared in such different fields as theoretical biology and cognitive psychology. Even if its interpretations are completely distinct, the theory of individual learning, including mimetic phenomena, turns out to make use of similar models and results as population dynamics. The fundamental idea — which needs to be made more explicit — is to interpret the probabilities that appear in “mixed” strategies not as proportions of individuals using the various pure strategies, but as propensities, for a single individual, to use these pure strategies. Moreover, it is possible to build hybrid models, with populations of learning individuals. Finally, even if the microeconomist is mainly interested by how interactive individuals learn, it cannot be excluded that population dynamics reveals useful to understand some specific social and economic problems.

经济代写|微观经济学代考Microeconomics代写|Definitions

All concepts will be introduced with the formalism of two-player normal form games. Let $X_1$ be the set of strategies available to player 1 and, likewise, let $X_2$ be player 2 strategy set (elements of these sets are “pure” strategies). For $x_1 \in X_1$ and $x_2 \in X_2$, the utilities associated with the strategy profile $\left(x_1, x_2\right)$ are denoted $u_1\left(x_1, x_2\right)$ for player 1 and $u_2\left(x_1, x_2\right)$ for player 2. A game is said to be symmetric if both players play the same role in that game, that is to say they have the same set of available strategies $\left(X_1=X_2=X\right)$ and the payoffs are such that $u_2\left(x_1, x_2\right)=u_1\left(x_2, x_1\right)$. The utility of a player choosing $x$ when the other player chooses $y$ is then simply denoted $u(x, y)$, thus $u(x, y)=u_1(x, y)=u_2(y, x)$.

In the technology game taken as an example, $X_1={A 1, B 1}, X_2={A 2, B 2}$, and the utilities are given by Table 3.1 :
$$
\begin{aligned}
& u_1(A 1, A 2)=2, u_1(A 1, B 2)=b, \
& u_1(B 1, A 2)=c, u_1(B 1, B 2)=4
\end{aligned}
$$
and likewise for player 2. The technology game can be seen as a symmetric game with $X={A, B}$.

If $p_1$ and $p_2$ are two probability distributions over $X_1$ and $X_2$ respectively (such probability distributions are called “mixed strategies”), one also denotes by $u_1$ the expected utility:
$$
\begin{gathered}
u_1\left(p_1, x_2\right)=\sum_{x \mid \in X_1} u_1\left(x_1, x_2\right) p_1\left(x_1\right) \
u_1\left(p_1, p_2\right)=\sum_{x_1 \in X_2} \sum_{x_2 \in X_2} u_1\left(x_1, x_2\right) p_1\left(x_1\right) p_2\left(x_2\right)
\end{gathered}
$$
and likewise for $u_2$. Note that the preceding definition leaves open the interpretation of the probabilities. They can be proportions of users in a population, individual propensity to use pure strategies, or temporal frequencies of the occurence of pure strategies.

微观经济学代写

经济代写|微观经济学代考MICROECONOMICS代写|SOME MODELS

从技术上讲，“进化论游戏”是由阶段游戏和动态过程定义的。阶段博亦以正常或扩展形式表述，仅定义与可能的行动组合相关的效用。动态过程 指定了对抗、信息、评估和决策的原则，这些原则在舞台博娈的重复中发挥作用。因此，通过指定动态，建模者可以引入她认为相关的实际过 程，处理最佳反应、学习、选择、模仿、强化等。
进化博栾论有两种贡献。一方面，该理论试图找到对系统时间行为的描述，这种描述不太依赖于所考虑的动态过程的细节。对于某些类别的“简 单”动态过程，已经获得了这样的结果，这些过程仅包含选择或强化机制，以及低强度的突变或探索机制。另一方面，进化论博栾论已经能够为某 些特定问题提供新的见解，例如技术的传播或制度的起源。几本专着对进化博恋论的技术成就进行了综述，例如 Maynard Smith1982, 威布尔1995, 天空有效值 1996, 维加-雷东多 1996, 萨缪尔森1997，年轻的1998或 Fudenberg 和 Levine1998.
进化博亦论的模型和解释在两个极端之间波动：种群动态和个体学习。在人口动态中，有大量的个体，每个人都被赋予了一种他无法控制的策 略。这种策略保持不变，除非突变是随机的且相对罕见。在一个群体中，策略用户比例的变化由选择过程引导，这有利于最合适的个体的繁殖。 相比之下，个人学习理论假设每个人都可以随时间改变他的策略。当这种变化包含一定程度的主动实验时，它是随机的。如果不是假设人数多，
并非没有引起一些混乱，最值得注意的是，类似的形式模型出现在理论生物学和认知心理学等不同领域。即使其解释完全不同，包括模仿现象在 内的个体学习理论最终还是利用了与种群动力学相似的模型和结果。基本思想 – 需要更加明确一一是将出现在“混合”策略中的概率解释为使用各 种纯策略的个人的比例，而是解释为单个个体使用这些纯策略的倾向。此外，可以建立混合模型，其中包含学习个体的群体。最后，即使微观经 济学家主要对互动个体的学习方式感兴趣,

经济代写|微观经济学代考MICROECONOMICS代写|DEFINITIONS

所有的概念都将以两人正常形式游戏的形式主义来介绍。让 $X_1$ 是参与者 1 可用的策略集，同样，让 $X_2$ 成为玩家 2 策略集 elementsofthesesetsare “pure” strategies. 为了 $x_1 \in X_1$ 和 $x_2 \in X_2$, 与策略配置文件相关的实用程序 $\left(x_1, x_2\right)$ 表示 $u_1\left(x_1, x_2\right)$ 对于玩家 1 和 $u_2\left(x_1, x_2\right)$ 对于玩家 2。如果两个玩家在该游戏中扮演相同的角色，则称该游戏是对称的，也就是说他们具有相同的可用策略集 $\left(X_1=X_2=X\right)$ 回报是这样的 $u_2\left(x_1, x_2\right)=u_1\left(x_2, x_1\right)$. 玩家选择的效用 $x$ 当其他玩家选择时 $y$ 然后简单地表示 $u(x, y) ，$ 因此 $u(x, y)=u_1(x, y)=u_2(y, x)$.
以科技游戏为例， $X_1=A 1, B 1, X_2=A 2, B 2$ ，实用程序由表 3.1 给出:
$$
u_1(A 1, A 2)=2, u_1(A 1, B 2)=b, \quad u_1(B 1, A 2)=c, u_1(B 1, B 2)=4
$$
玩家 2 也是如此。技术博恋可以看作是一个对称博栾 $X=A, B$.
如果 $p_1$ 和 $p_2$ 是两个概率分布 $X_1$ 和 $X_2$ 分别suchprobabilitydistributionsarecalled “mixedstrategies”,一个也表示为 $u_1$ 预期效用:
$$
u_1\left(p_1, x_2\right)=\sum_{x \mid \in X_1} u_1\left(x_1, x_2\right) p_1\left(x_1\right) u_1\left(p_1, p_2\right)=\sum_{x_1 \in X_2} \sum_{x_2 \in X_2} u_1\left(x_1, x_2\right) p_1\left(x_1\right) p_2\left(x_2\right)
$$
同样对于 $u_2$. 请注意，前面的定义末对概率进行解释。它们可以是人口中用户的比例、使用纯策略的个人倾向或纯策略出现的时间频率。

经济代写|微观经济学代考Microeconomics代写 请认准exambang™. exambang™为您的留学生涯保驾护航。

微观经济学代写

微观经济学是主流经济学的一个分支，研究个人和企业在做出有关稀缺资源分配的决策时的行为以及这些个人和企业之间的相互作用。my-assignmentexpert™ 为您的留学生涯保驾护航 在数学Mathematics作业代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的数学Mathematics代写服务。我们的专家在图论代写Graph Theory代写方面经验极为丰富，各种图论代写Graph Theory相关的作业也就用不着 说。

线性代数代写

线性代数是数学的一个分支，涉及线性方程，如：线性图，如：以及它们在向量空间和通过矩阵的表示。线性代数是几乎所有数学领域的核心。

博弈论代写

现代博弈论始于约翰-冯-诺伊曼（John von Neumann）提出的两人零和博弈中的混合策略均衡的观点及其证明。冯-诺依曼的原始证明使用了关于连续映射到紧凑凸集的布劳威尔定点定理，这成为博弈论和数学经济学的标准方法。在他的论文之后，1944年，他与奥斯卡-莫根斯特恩（Oskar Morgenstern）共同撰写了《游戏和经济行为理论》一书，该书考虑了几个参与者的合作游戏。这本书的第二版提供了预期效用的公理理论，使数理统计学家和经济学家能够处理不确定性下的决策。

微积分代写

微积分，最初被称为无穷小微积分或 “无穷小的微积分”，是对连续变化的数学研究，就像几何学是对形状的研究，而代数是对算术运算的概括研究一样。

它有两个主要分支，微分和积分；微分涉及瞬时变化率和曲线的斜率，而积分涉及数量的累积，以及曲线下或曲线之间的面积。这两个分支通过微积分的基本定理相互联系，它们利用了无限序列和无限级数收敛到一个明确定义的极限的基本概念 。

计量经济学代写

什么是计量经济学？
计量经济学是统计学和数学模型的定量应用，使用数据来发展理论或测试经济学中的现有假设，并根据历史数据预测未来趋势。它对现实世界的数据进行统计试验，然后将结果与被测试的理论进行比较和对比。

根据你是对测试现有理论感兴趣，还是对利用现有数据在这些观察的基础上提出新的假设感兴趣，计量经济学可以细分为两大类：理论和应用。那些经常从事这种实践的人通常被称为计量经济学家。

Matlab代写

MATLAB 是一种用于技术计算的高性能语言。它将计算、可视化和编程集成在一个易于使用的环境中，其中问题和解决方案以熟悉的数学符号表示。典型用途包括：数学和计算算法开发建模、仿真和原型制作数据分析、探索和可视化科学和工程图形应用程序开发，包括图形用户界面构建MATLAB 是一个交互式系统，其基本数据元素是一个不需要维度的数组。这使您可以解决许多技术计算问题，尤其是那些具有矩阵和向量公式的问题，而只需用 C 或 Fortran 等标量非交互式语言编写程序所需的时间的一小部分。MATLAB 名称代表矩阵实验室。MATLAB 最初的编写目的是提供对由 LINPACK 和 EISPACK 项目开发的矩阵软件的轻松访问，这两个项目共同代表了矩阵计算软件的最新技术。MATLAB 经过多年的发展，得到了许多用户的投入。在大学环境中，它是数学、工程和科学入门和高级课程的标准教学工具。在工业领域，MATLAB 是高效研究、开发和分析的首选工具。MATLAB 具有一系列称为工具箱的特定于应用程序的解决方案。对于大多数 MATLAB 用户来说非常重要，工具箱允许您学习和应用专业技术。工具箱是 MATLAB 函数（M 文件）的综合集合，可扩展 MATLAB 环境以解决特定类别的问题。可用工具箱的领域包括信号处理、控制系统、神经网络、模糊逻辑、小波、仿真等。