MY-ASSIGNMENTEXPERT™可以为您提供mathstat MATH2300 Mathematical Modeling数学建模的代写代考和辅导服务!
这是戴尔豪斯大学数学建模课程的代写成功案例。
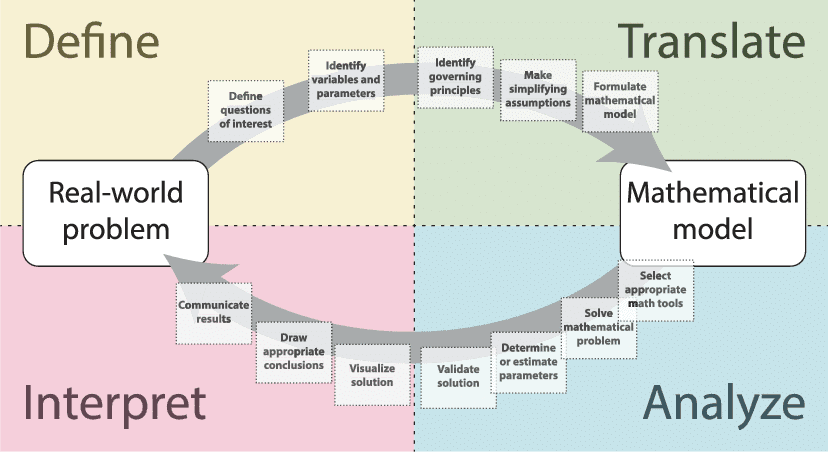
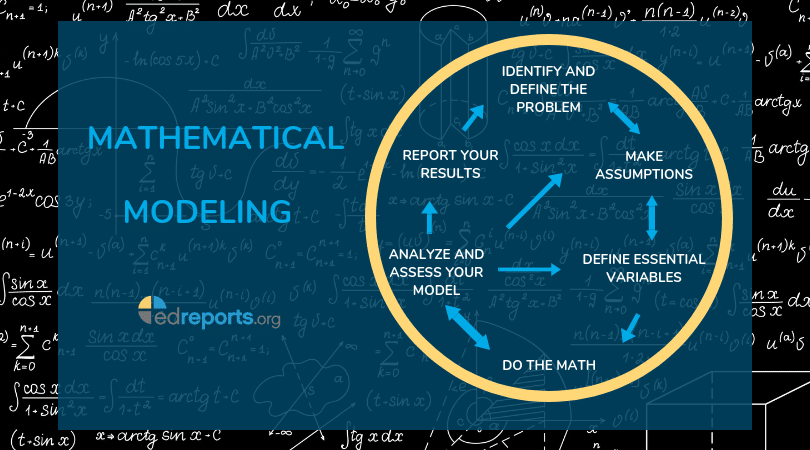
MATH2300课程简介
(3) Credit Hours
Lab-based activities designed to strengthen and expand knowledge of topics in secondary mathematics, focusing on topics from precalculus and elementary calculus. Explorations will involve the use of multiple representations, transformations, data analysis techniques and interconnections among geometry, probability and algebra. Most labs will include significant use of various technologies. The use of quantitative approaches and building relationships between discrete and continuous reasoning will be recurrent themes. Every semester. Prerequisites: Admissions to the UTeaChattanooga program; university, UTSM, and major department grade point averages of at least 2.5; UTSM 1020 and MATH 1920, MATH 1921 and MATH 2200 with minimum grades of C or UTeaChattanooga Co-Director approval.
Prerequisites
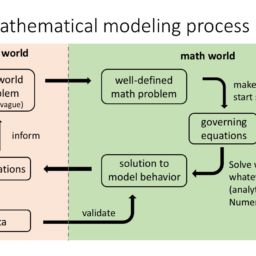
Course outline: Dynamical systems, basic probability, queing theory, selected topics.
References: The textbook for this course is “A Course in Mathematical Modeling” by Mooney and Swift. Some of the material will be outside the textbook in which case appropriate references will be provided.
Advising and Access Services Center: Students may request accommodation as a result of barriers related to disability, religious obligation, or any characteristic under the Nova Scotia Human Rights Act. Students who require academic accommodation for either classroom participation or the writing of tests and exams should make their request to the Advising and Access Services Center (AASC) prior to or at the outset of the regular academic year. Please visit www.dal.ca/access for more information and to obtain the Request for Accommodation – Form A.
MATH2300 Mathematical Modeling HELP(EXAM HELP, ONLINE TUTOR)
Consider the dynamical $x_{n+2}=x_n-2 x_{n+1}$ with $x_0=0$ and $x_1=1$.
(a) Compute $x_1$ to $x_5$ (by hand).
(b) Using any method you like, find an explicit formula for $x_n$. Verify your formula by comparing to part (a).
(c) Using formula in part (b), estimate $\log \left(\left|x_{2300}\right|\right)$.
An insect population is divided into three age classes, ages 0,1 and 2. During each time period $20 \%$ of the females of age 0 and $70 \%$ of the females of age 1 survive until the end of the following breeding season. Females of age 1 have an average fecundity of 3.2 offspring per female and the average fecundity of age 2 females is 1.7. No female lives beyond three years.
(a) Draw a transition diagram and set up a dynamical system to describe this situation.
(b) If initially the population consists of 2000 females of age 0,800 females of age 1 , and 200 females of age 2 , find the age distribution after three years.
(c) Use Matlab to plot the population of each age class in years 0 to 20.
(d) Use the matlab command eig to compute the relevant eigenvalues and answer the following questions. (d1) Is the population sustainable? In other words, does it survive as $t \rightarrow \infty$ ? (d2) Determine the long-time distribution the population. In other words, what fraction of the population belongs to each class after a long time?
A regional rent-a-car company has offices in Lincoln, Omaha and ten other small cities. Their records show that each week, $55 \%$ of the cars rented in Lincoln returned to Lincoln, 35\% are returned to Omaha and the remaining cars are returned elsewhere. Of those rented in Omaha, $75 \%$ are returned to Omaha, $5 \%$ to Lincoln and $20 \%$ elsewhere. Of the cars rented in the ten other cities, $25 \%$ are returned to Omaha and $5 \%$ to Lincoln.
(a) Draw a graph illustrating the states and the transition probabilities.
(b) Set up a dynamical system (using transition matrices) which models this situation. Using Matlab, simulate your system. Start with $100 \%$ of the cars in Lincoln, and output the fraction of the cars in each of Lincoln, Omaha and elsewhere each week. How many weeks are required until the system is roughly at the steady state? What is that steady state? Hand in your code and output.
(c) Compute the steady state analytically.
Two balls are distributed between two urns labelled A and B. Each turn one of the two balls is selected at random with equal probability and moved to the other urn.
(a) Formulate this problem as a dynamical system for the three possible states of urn A. Dont forget to sketch a transition diagram.
(b) In the long run, what fraction of the time is urn A empty?

MY-ASSIGNMENTEXPERT™可以为您提供MATHSTAT MATH2300 MATHEMATICAL MODELING数学建模的代写代考和辅导服务!