MY-ASSIGNMENTEXPERT™可以为您提供engineering MATH4604 Finite Element MethoD有限元方法的代写代考和辅导服务!
这是普渡大學有限元方法的代写成功案例。

CE595课程简介
• Academic integrity is expected of all students at all times. Further information on academic integrity policies may be found in the handbook University Regulations and on the Web at http://www.purdue.edu/ODOS/osrr/integrity.htm.
• Homework is due in class on the date indicated. In general, no late homework will be accepted. If you feel that you have serious extenuating circumstances (eg., illnesses or accidents requiring medical attention, personal or family crises), you must discuss your situation with Dr. Varma as soon as possible. In particular, foreseeable conflicts with due dates (eg., interviews, participation in sports activities, religious observances, etc.) must be brought to our attention before the due date.
• It is anticipated, even encouraged, that students will consult with each other on homework assignments. It is expected, however, that all work submitted by the student represent his/her own effort. Instances of plagiarism on an assignment will result in full loss of credit for that assignment.
• Instances of cheating in any form during an exam will result in full loss of credit for that exam. Additional measures, including immediate failure of the course, may be applied at the discretion of the instructor and/or University staff.
• Students who have documented disabilities and require accommodations must make an appointment with Dr. Varma to discuss their needs by the end of the second week of class. Students with disabilities must be registered with Adaptive Programs in the Office of the Dean of Students before classroom accommodations can be provided.
Prerequisites
Grades will be based upon the following elements:
• Homework (25% of total grade) Due in class at dates to be announced.
• Hourly Exam #1 (25% of total grade) Tentatively scheduled for February last week.
• Hourly Exam #2 (25% of total grade) Tentatively scheduled for April first week.
• Course Project or Final Exam (25% of total grade) Schedule will be announced later in the semester.
CE595 Finite Element Method HELP(EXAM HELP, ONLINE TUTOR)
Assume that the axial displacement $u(x)$ and transverse displacement $w(x)$ of the Bernoulli-Euler beam of Example 2.3.2 are of the form
$$
\begin{aligned}
u(x)= & \left(1-\frac{x}{L}\right) u_1+\frac{x}{L} u_2 \equiv \psi_1(x) u_1+\psi_2(x) u_2 \
w(x)= & {\left[1-3\left(\frac{x}{L}\right)^2+2\left(\frac{x}{L}\right)^3\right] w_1-x\left(1-\frac{x}{L}\right)^2 \theta_1 } \
& +\left[3\left(\frac{x}{L}\right)^2-2\left(\frac{x}{L}\right)^3\right] w_2-x\left[\left(\frac{x}{L}\right)^2-\frac{x}{L}\right] \theta_2 \
\equiv & \varphi_1(x) w_1+\varphi_2(x) \theta_1+\varphi_3(x) w_2+\varphi_4(x) \theta_2
\end{aligned}
$$
where $\left(u_1, u_2, w_1, w_2\right)$ and $\left(\theta_1, \theta_2\right)$ are the displacements and rotations of the two ends of the beam, as shown in Fig. 2.3.5. Express the strain energy of the Bernoulli-Euler beam theory in terms of the parameters $\left(u_1, w_1, \theta_1\right)$ and $\left(u_2, w_2, \theta_2\right)$.
Solution: The strain energy for the Bernoulli-Euler beam is given by Eq. (2.3.10). First we compute $d u / d x$ and $d_2 w / d x_2$ in terms of the generalized displacements $\left(u_1, u_2, w_1, w_2, \theta_1, \theta_2\right)$ :
$$
\begin{aligned}
\frac{d u}{d x} & =\frac{u_2-u_1}{L}, \
\frac{d^2 w}{d x^2} & =-\frac{6}{L^2}\left(1-2 \frac{x}{L}\right) w_1-\frac{2}{L}\left(3 \frac{x}{L}-2\right) \theta_1+\frac{6}{L^2}\left(1-2 \frac{x}{L}\right) w_2-\frac{2}{L}\left(3 \frac{x}{L}-1\right) \theta_2
\end{aligned}
$$
Then the strain energy due to stretching is
$$
U_s=\frac{E A}{2} \int_0^L\left(\frac{d u}{d x}\right)^2 d x=\frac{E A}{2 L}\left(u_2-u_1\right)^2=\frac{E A}{2 L}\left{\begin{array}{l}
u_1 \
u_2
\end{array}\right}^{\mathrm{T}}\left[\begin{array}{rr}
1 & -1 \
-1 & 1
\end{array}\right]\left{\begin{array}{l}
u_1 \
u_2
\end{array}\right}
$$
Next, we evaluate the integrals $(\xi=x / L$ and $d x=L d \xi)$ :
$$
\begin{aligned}
& \int_0^1(1-2 \xi)^2 L d \xi=\frac{L}{3}, \quad \int_0^1(1-2 \xi)(3 \xi-2) L d \xi=-\frac{L}{2} \
& \int_0^1(3 \xi-2)^2 L d \xi=L, \quad \int_0^1(1-2 \xi)(3 \xi-1) L d \xi=-\frac{L}{2} \
& \int_0^1(3 \xi-1)^2 L d \xi=L, \quad \int_0^1(3 \xi-2)(3 \xi-1) L d \xi=\frac{L}{2}
\end{aligned}
$$
Then the strain energy due to bending is
$$
\begin{aligned}
U_b= & \frac{E I}{2} \int_0^L\left(\frac{d^2 w}{d x^2}\right)^2 d x \
= & \frac{E I}{L^3}\left(6 w_1^2-6 L w_1 \theta_1-12 w_1 w_2-6 L w_1 \theta_2+2 L^2 \theta_1^2+6 L \theta_1 w_2\right. \
& \left.+2 L^2 \theta_1 \theta_2+6 w_2^2+6 L w_2 \theta_2+2 L^2 \theta_2^2\right) \
= & \frac{E I}{L^3}\left{\begin{array}{c}
w_1 \
\theta_1 \
w_2 \
\theta_2
\end{array}\right}\left[\begin{array}{rrrr}
-3 L & -6 & -3 L \
-3 L & 2 L^2 & 3 L & L^2 \
-6 & 3 L & 6 & 3 L \
-3 L & L^2 & 3 L & 2 L^2
\end{array}\right]\left{\begin{array}{c}
w_1 \
\theta_1 \
w_2 \
\theta_2
\end{array}\right}
\end{aligned}
$$
Thus, the strain energy due to stretching and bending of the beam $\left(U=U_s+\right.$ $U_b$ ) is
$$
\begin{aligned}
& U=\left{\begin{array}{l}
u_1 \
u_2
\end{array}\right}^{\mathrm{T}} \frac{E A}{2 L}\left[\begin{array}{rr}
1 & -1 \
-1 & 1
\end{array}\right]\left{\begin{array}{l}
u_1 \
u_2
\end{array}\right} \
&+\left{\begin{array}{c}
w_1 \
\theta_1 \
w_2 \
\theta_2
\end{array}\right} \frac{E I}{L^3}\left[\begin{array}{rrrr}
6 & -3 L & -6 & -3 L \
-3 L & 2 L^2 & 3 L & L^2 \
-6 & 3 L & 6 & 3 L \
-3 L & L^2 & 3 L & 2 L^2
\end{array}\right]\left{\begin{array}{c}
w_1 \
\theta_1 \
w_2 \
\theta_2
\end{array}\right}
\end{aligned}
$$
We have discussed the kinematics of the Bernoulli-Euler beam theory. Use the principle of virtual displacements to derive the governing equations of the Bernoulli-Euler beam theory. Assume that the beam rests on a linear elastic foundation with foundation modulus $k$ and subjected to a distributed longitudinal load $f(x)$ and transverse load $q(x)$ .
Solution: The displacement field of a beam under the Bernoulli-Euler kinematic hypothesis is given by [see Eq. (2.3.7)]
$$
u_1(x, y, z)=u(x)+z \theta_x, u_2=0, u_3(x, y, z)=w(x) ; \quad \theta_x \equiv-\frac{d w}{d x}
$$
If we assume that the strains are small, the only nonzero strain is given by
$$
\varepsilon_{x x}=\frac{d u}{d x}+z \frac{d \theta_x}{d x}=\frac{d u}{d x}-z \frac{d^2 w}{d x^2}
$$
Let the virtual displacements be $\delta u$ and $\delta w$, which are completely arbitrary because there are no specified geometric boundary conditions for the problem at hand. Then the virtual strain $\delta \varepsilon_{x x}$ is given by
$$
\delta \varepsilon_{x x}=\delta\left(\frac{d u}{d x}+z \frac{d \theta_x}{d x}\right)=\frac{d \delta u}{d x}+z \frac{d \delta \theta_x}{d x}
$$
Then the internal and external virtual works due to the virtual displacements $\delta u$ and $\delta w$ are given by
$$
\begin{aligned}
\delta W_E= & -\left{\int_0^L\left[f(x) \delta u+q(x) \delta w\left(x, h_t\right)\right] d x+\int_0^L\left(-F_s\right) \delta w\left(x, h_b\right) d x\right. \
& +P \delta u(L)+F \delta w(L)} \
= & -\left{\int_0^L[f(x) \delta u+q(x) \delta w(x)] d x-\int_0^L k w(x) \delta w(x) d x\right. \
& +P \delta u(L)+F \delta w(L)}
\end{aligned}
$$
$$
\begin{aligned}
\delta W_I & =\int_0^L \int_A \sigma_{x x} \delta \varepsilon_{x x} d x d A \
& =\int_0^L \int_A \sigma_{x x}\left(\frac{d \delta u}{d x}-z \frac{d^2 \delta w}{d x^2}\right) d x d A
\end{aligned}
$$
where $L$ is the length, $h_t$ is the distance from the $x$-axis to the top of the beam, $h_b$ is the distance from the $x$-axis to the bottom of the beam, and $A$ is the cross-sectional area of the beam. The foundation reaction force $F_s$ (acting downward) is replaced with $F_s=k w(x)$ using the linear elastic constitutive equation for the foundation.
The principle of virtual displacements requires that $\delta W=\delta W_I+\delta W_E=0$, which gives
$$
\begin{aligned}
0= & \int_0^L \int_A \sigma_{x x}\left(\frac{d \delta u}{d x}-z \frac{d^2 \delta w}{d x^2}\right) d A d x \
& -\int_0^L[f \delta u+(q-k w) \delta w] d x-P \delta u(L)-F \delta w(L) \
= & \int_0^L\left(N \frac{d \delta u}{d x}-M \frac{d^2 \delta w}{d x^2}\right) d x-\int_0^L[f \delta u+(q-k w) \delta w] d x \
& -P \delta u(L)-F \delta w(L) \
= & \int_0^L\left(-\frac{d N}{d x} \delta u-\frac{d^2 M}{d x^2} \delta w\right) d x-\int_0^L[f \delta u+(q-k w) \delta w] d x \
& -P \delta u(L)-F \delta w(L)+\left[N \delta u+\frac{d M}{d x} \delta w-M \frac{d \delta w}{d x}\right]0^L \end{aligned} $$ where $N$ and $M$ are the stress resultants defined by $$ N=\int_A \sigma{x x} d A, M=\int_A \sigma_{x x} z d A
$$
The Euler equations are obtained by setting the coefficients of $\delta u$ and $\delta w$ under the integral separately to zero:
$$
\delta u: \quad-\frac{d N}{d x}=f
$$
$$
\delta w: \quad-\frac{d^2 M}{d x^2}+k w=q
$$
in $0<x<L$.
We note that $\delta u, \delta w$, and $d \delta w / d x=\delta(d w / d x)$ appear in the boundary terms. Hence, $u, w$, and $(d w / d x)$ are the primary variables of the theory, and their specification constitutes the displacement, geometric, or essential boundary conditions. Since nothing is said about the primary variables being specified, $\delta u, \delta w$, and $d \delta w / d x$ are arbitrary at
$$
\begin{aligned}
& N=0, \quad V \equiv \frac{d M}{d x}=0, \quad M=0 \text { at } x=0 \
& N=P, \quad \frac{d M}{d x}=F, \quad M=0 \text { at } x=L
\end{aligned}
$$
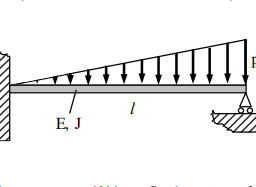
Use Castigliano’s theorem I to determine the force-displacement relationships between the generalized displacements and forces of a straight beam of length $L$ and constant bending stiffness $E I$ shown in Fig. 2.3.10.
Fig. 2.3.10 Pure bending of a beam. (a) Generalized displacements. (b) Generalized forces.
Solution: The strain energy of a straight beam in pure bending according to the Euler-Bernoulli beam theory is given in terms of the generalized end displacements $w_1, \theta_1, w_2$, and $\theta_2$ in Eq. (6) of Example 2.3.3 as
$$
\begin{aligned}
U= & \frac{E I}{L^3}\left(6 w_1^2-6 L w_1 \theta_1-12 w_1 w_2-6 L w_1 \theta_2+2 L^2 \theta_1^2+6 L \theta_1 w_2\right. \
& \left.+2 L^2 \theta_1 \theta_2+6 w_2^2+6 L w_2 \theta_2+2 L^2 \theta_2^2\right)
\end{aligned}
$$
Then by Castigliano’s theorem I, we have
$$
\begin{aligned}
& F_1=\frac{\partial U}{\partial w_1}=\frac{E I}{L^3}\left(12 w_1-6 L \theta_1-12 w_2-6 L \theta_2\right) \
& M_1=\frac{\partial U}{\partial \theta_1}=\frac{E I}{L^3}\left(-6 L w_1+4 L^2 \theta_1+6 L w_2+2 L^2 \theta_2\right) \
& F_2=\frac{\partial U}{\partial w_2}=\frac{E I}{L^3}\left(-12 w_1+6 L \theta_1+12 w_2+6 L \theta_2\right) \
& M_2=\frac{\partial U}{\partial \theta_2}=\frac{E I}{L^3}\left(-6 L w_1+2 L^2 \theta_1+6 L w_2+4 L^2 \theta_2\right)
\end{aligned}
$$
which can be expressed in matrix form as
$$
\left{\begin{array}{c}
F_1 \
M_1 \
F_2 \
M_2
\end{array}\right}=\frac{2 E I}{L^3}\left[\begin{array}{rrrr}
6 & -3 L & -6 & -3 L \
-3 L & 2 L^2 & 3 L & L^2 \
-6 & 3 L & 6 & 3 L \
-3 L & L^2 & 3 L & 2 L^2
\end{array}\right]\left{\begin{array}{c}
w_1 \
\theta_1 \
w_2 \
\theta_2
\end{array}\right}
$$

MY-ASSIGNMENTEXPERT™可以为您提供ENGINEERING MATH4604 FINITE ELEMENT METHOD有限元方法的代写代考和辅导服务!