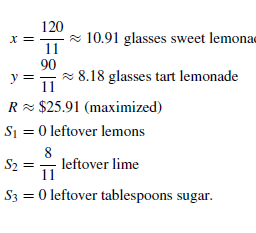数学代写|Nonparametric distribution estimation 凸优化代考
凸优化代写
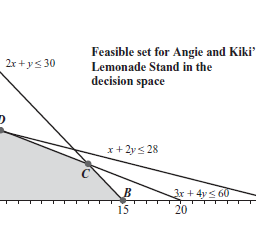
We consider a random variable $X$ with values in the finite set $\left{\alpha_{1}, \ldots, \alpha_{n}\right} \subseteq \mathbf{R}$. (We take the values to be in $\mathbf{R}$. for simplicity; the same ideas can be applied when the values are in $\mathbf{R}^{k}$, for example.) The distribution of $X$ is characterized by $p \in \mathbf{R}^{n}$, with $\operatorname{prob}\left(X=\alpha_{k}\right)=p_{k}$. Clearly, $p$ satisfies $p \succeq 0,1^{T} p=1$. Conversely, if $p \in \mathbf{R}^{n}$ satisfies $p \succeq 0,1^{T} p=1$, then it defines a probability distribution for a random variable $X$, defined as $\operatorname{prob}\left(X=\alpha_{k}\right)=p_{k}$. Thus, the probability simplex
$$
\left{p \in \mathbf{R}^{n} \mid p \succeq 0,1^{T} p=1\right}
$$
7 Statistical estimation
360
is in one-to-one correspondence with all possible probability distributions for a random variable $X$ taking values in $\left{\alpha_{1}, \ldots, \alpha_{n}\right}$. In this section we discuss methods used to estimate the distribution $p$ based on a combination of prior information and, possibly, observations and measurements. Prior information
Many types of prior information about p can be expressed in terms of linear equality constraints or inequalities. If $f: \mathbf{R} \rightarrow \mathbf{R}$, is any function, then
$$
\mathbf{E} f(X)=\sum_{i=1}^{n} p_{1} f\left(\alpha_{1}\right)
$$
is a linear function of $p$. As a special case, if $C \subseteq \mathbf{R}$, then prob $(X \in C)$ is a linear function of $p$ :
凸优化代考
我们考虑一个随机变量 $X$,其值在有限集合 $\left{\alpha_{1}, \ldots, \alpha_{n}\right} \subseteq \mathbf{R}$ 中。 (为了简单起见,我们取值在 $\mathbf{R}$ 中;例如,当值在 $\mathbf{R}^{k}$ 中时,可以应用相同的想法。)$ 的分布X$ 的特征是 $p \in \mathbf{R}^{n}$,其中 $\operatorname{prob}\left(X=\alpha_{k}\right)=p_{k}$。显然,$p$ 满足 $p \succeq 0,1^{T} p=1$。相反,如果 $p \in \mathbf{R}^{n}$ 满足 $p \succeq 0,1^{T} p=1$,那么它定义了随机变量 $X$ 的概率分布,定义为$\operatorname{prob}\left(X=\alpha_{k}\right)=p_{k}$。因此,概率单纯形
$$
\left{p \in \mathbf{R}^{n} \mid p \succeq 0,1^{T} p=1\right}
$$
7 统计估计
360
与取值在 $\left{\alpha_{1}, \ldots, \alpha_{n}\right}$ 中的随机变量 $X$ 的所有可能概率分布一一对应。在本节中,我们讨论用于根据先验信息以及可能的观察和测量的组合来估计分布 $p$ 的方法。先验信息
关于 p 的许多类型的先验信息可以用线性等式约束或不等式来表示。如果 $f: \mathbf{R} \rightarrow \mathbf{R}$, 是任何函数,那么
$$
\mathbf{E} f(X)=\sum_{i=1}^{n} p_{1} f\left(\alpha_{1}\right)
$$
是 $p$ 的线性函数。作为一种特殊情况,如果 $C \subseteq \mathbf{R}$,那么概率 $(X \in C)$ 是 $p$ 的线性函数:

数学代写| Chebyshev polynomials 数值分析代考 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。
时间序列分析代写
统计作业代写
随机过程代写
随机过程,是依赖于参数的一组随机变量的全体,参数通常是时间。 随机变量是随机现象的数量表现,其取值随着偶然因素的影响而改变。 例如,某商店在从时间t0到时间tK这段时间内接待顾客的人数,就是依赖于时间t的一组随机变量,即随机过程