如果你也在 怎样代写微积分Calculus 这个学科遇到相关的难题,请随时右上角联系我们的24/7代写客服。微积分Calculus 最初被称为无穷小微积分或 “无穷小的微积分”,是对连续变化的数学研究,就像几何学是对形状的研究,而代数是对算术运算的概括研究一样。
微积分Calculus 它有两个主要分支,微分和积分;微分涉及瞬时变化率和曲线的斜率,而积分涉及数量的累积,以及曲线下或曲线之间的面积。这两个分支通过微积分的基本定理相互关联,它们利用了无限序列和无限数列收敛到一个明确定义的极限的基本概念 。17世纪末,牛顿(Isaac Newton)和莱布尼兹(Gottfried Wilhelm Leibniz)独立开发了无限小数微积分。后来的工作,包括对极限概念的编纂,将这些发展置于更坚实的概念基础上。今天,微积分在科学、工程和社会科学中得到了广泛的应用。
同学们在留学期间,都对各式各样的作业考试很是头疼,如果你无从下手,不如考虑my-assignmentexpert™!
my-assignmentexpert™提供最专业的一站式服务:Essay代写,Dissertation代写,Assignment代写,Paper代写,Proposal代写,Proposal代写,Literature Review代写,Online Course,Exam代考等等。my-assignmentexpert™专注为留学生提供Essay代写服务,拥有各个专业的博硕教师团队帮您代写,免费修改及辅导,保证成果完成的效率和质量。同时有多家检测平台帐号,包括Turnitin高级账户,检测论文不会留痕,写好后检测修改,放心可靠,经得起任何考验!
微积分Calculus 代写,免费提交作业要求, 满意后付款,成绩80\%以下全额退款,安全省心无顾虑。专业硕 博写手团队,所有订单可靠准时,保证 100% 原创。 最高质量的微积分Calculus 作业代写,服务覆盖北美、欧洲、澳洲等 国家。 在代写价格方面,考虑到同学们的经济条件,在保障代写质量的前提下,我们为客户提供最合理的价格。 由于作业种类很多,同时其中的大部分作业在字数上都没有具体要求,因此微积分Calculus 作业代写的价格不固定。通常在专家查看完作业要求之后会给出报价。作业难度和截止日期对价格也有很大的影响。
想知道您作业确定的价格吗? 免费下单以相关学科的专家能了解具体的要求之后在1-3个小时就提出价格。专家的 报价比上列的价格能便宜好几倍。
我们在数学Mathematics代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的数学Mathematics代写服务。我们的专家在微积分Calculus Assignment代写方面经验极为丰富,各种微积分Calculus Assignment相关的作业也就用不着 说。
数学代写|微积分代写Calculus代考|The Graph and Range of $\ln x$
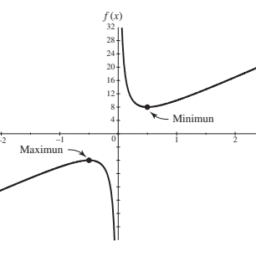
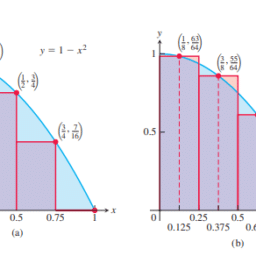
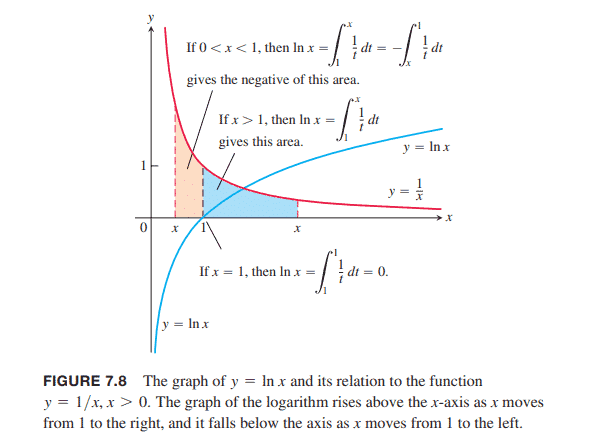
The derivative $d(\ln x) / d x=1 / x$ is positive for $x>0$, so $\ln x$ is an increasing function of $x$. The second derivative, $-1 / x^2$, is negative, so the graph of $\ln x$ is concave down. (See Figure 7.9a.)
We can estimate the value of $\ln 2$ by considering the area under the graph of $y=1 / x$ and above the interval $[1,2]$. In Figure 7.9(b) a rectangle of height $1 / 2$ over the interval $[1,2]$ fits under the graph. Therefore the area under the graph, which is $\ln 2$, is greater than the area, $1 / 2$, of the rectangle. So $\ln 2>1 / 2$. Knowing this we have
$$
\ln 2^n=n \ln 2>n\left(\frac{1}{2}\right)=\frac{n}{2} .
$$
This result shows that $\ln \left(2^n\right) \rightarrow \infty$ as $n \rightarrow \infty$. Since $\ln x$ is an increasing function, we get that
$$
\lim {x \rightarrow \infty} \ln x=\infty . \quad \ln x \text { increasing, not bounded above } $$ We also have $$ \lim {x \rightarrow 0^{+}} \ln x=\lim {t \rightarrow \infty} \ln t^{-1}=\lim {t \rightarrow \infty}(-\ln t)=-\infty . \quad x=1 / t=t^{-1}
$$
We defined $\ln x$ for $x>0$, so the domain of $\ln x$ is the set of positive real numbers. The above discussion and the Intermediate Value Theorem show that its range is the entire real line, giving the graph of $y=\ln x$ shown in Figure 7.9(a).
The Integral $\int(1 / u) d u$
Example 2c leads to the following integral formula.
If $u$ is a differentiable function that is never zero, then
$$
\int \frac{1}{u} d u=\ln |u|+C .
$$
Equation (3) applies anywhere on the domain of $1 / u$, which is the set of points where $u \neq 0$. It says that integrals that have the form $\int d u / u$ lead to logarithms. Whenever $u=f(x)$ is a differentiable function that is never zero, we have that $d u=f^{\prime}(x) d x$ and
$$
\int \frac{f^{\prime}(x)}{f(x)} d x=\ln |f(x)|+C
$$
数学代写|微积分代写Calculus代考|The Integrals of $\tan x, \cot x, \sec x$, and $\csc x$
Equation (3) tells us how to integrate these trigonometric functions.
$$
\begin{aligned}
\int \tan x d x & =\int \frac{\sin x}{\cos x} d x=\int \frac{-d u}{u} & \begin{array}{l}
u=\cos x>0 \text { on }(-\pi / 2, \pi / 2), \
d u=-\sin x d x
\end{array} \
& =-\ln |u|+C=-\ln |\cos x|+C & \
& =\ln \frac{1}{|\cos x|}+C=\ln |\sec x|+C . & \text { Reciprocal Rule }
\end{aligned}
$$
For the cotangent,
$$
\begin{aligned}
\int \cot x d x & =\int \frac{\cos x d x}{\sin x}=\int \frac{d u}{u} \quad \begin{array}{l}
u=\sin x \
d u=\cos x d x
\end{array} \
& =\ln |u|+C=\ln |\sin x|+C=-\ln |\csc x|+C .
\end{aligned}
$$
To integrate $\sec x$, we multiply and divide by $(\sec x+\tan x)$ as an algebraic form of 1 .
$$
\begin{aligned}
& \int \sec x d x=\int \sec x \frac{(\sec x+\tan x)}{(\sec x+\tan x)} d x=\int \frac{\sec ^2 x+\sec x \tan x}{\sec x+\tan x} d x \
& =\int \frac{d u}{u}=\ln |u|+C=\ln |\sec x+\tan x|+C \quad \begin{array}{ll}
u=\sec x+\tan x \
d u=\left(\sec x \tan x+\sec ^2 x\right) d x
\end{array}
\end{aligned}
$$
For $\csc x$, we multiply and divide by $(\csc x+\cot x)$.
$$
\begin{aligned}
& \int \csc x d x=\int \csc x \frac{(\csc x+\cot x)}{(\csc x+\cot x)} d x=\int \frac{\csc ^2 x+\csc x \cot x}{\csc x+\cot x} d x \
& =\int \frac{-d u}{u}=-\ln |u|+C=-\ln |\csc x+\cot x|+C \quad u=\csc x+\cot x \
& d u=\left(-\csc x \cot x-\csc ^2 x\right) d x
\end{aligned}
$$
Integrals of the tangent, cotangent, secant, and cosecant functions
$$
\begin{array}{ll}
\int \tan u d u=\ln |\sec u|+C & \int \sec u d u=\ln |\sec u+\tan u|+C \
\int \cot u d u=\ln |\sin u|+C & \int \csc u d u=-\ln |\csc u+\cot u|+C
\end{array}
$$
微积分代写
数学代写|微积分代写Calculus代考|The Graph and Range of $\ln x$
$x>0$的导数$d(\ln x) / d x=1 / x$是正的,所以$\ln x$是$x$的递增函数。二阶导数$-1 / x^2$是负的,所以$\ln x$的曲线是向下凹的。(参见图7.9a。)
我们可以通过考虑$y=1 / x$图下和区间$[1,2]$上方的面积来估计$\ln 2$的值。在图7.9(b)中,在区间$[1,2]$上有一个高度为$1 / 2$的矩形拟合在图下。因此,图形下的面积$\ln 2$大于矩形的面积$1 / 2$。所以$\ln 2>1 / 2$。知道了这一点
$$
\ln 2^n=n \ln 2>n\left(\frac{1}{2}\right)=\frac{n}{2} .
$$
这个结果表明$\ln \left(2^n\right) \rightarrow \infty$等于$n \rightarrow \infty$。因为$\ln x$是一个递增函数,所以我们得到
$$
\lim {x \rightarrow \infty} \ln x=\infty . \quad \ln x \text { increasing, not bounded above } $$我们还有$$ \lim {x \rightarrow 0^{+}} \ln x=\lim {t \rightarrow \infty} \ln t^{-1}=\lim {t \rightarrow \infty}(-\ln t)=-\infty . \quad x=1 / t=t^{-1}
$$
我们为$x>0$定义了$\ln x$,所以$\ln x$的定义域是正实数的集合。由上述讨论和中间值定理可知,它的取值范围是整条实线,得到如图7.9(a)所示的$y=\ln x$图。
积分$\int(1 / u) d u$
例2c的积分公式如下。
如果$u$是一个不为零的可微函数,则
$$
\int \frac{1}{u} d u=\ln |u|+C .
$$
式(3)适用于$1 / u$域上的任意点,即$u \neq 0$。它说,形式为$\int d u / u$的积分会得到对数。当$u=f(x)$是一个不为零的可微函数时,我们有$d u=f^{\prime}(x) d x$和
$$
\int \frac{f^{\prime}(x)}{f(x)} d x=\ln |f(x)|+C
$$
数学代写|微积分代写Calculus代考|The Integrals of $\tan x, \cot x, \sec x$, and $\csc x$
式(3)告诉我们如何积分这些三角函数。
$$
\begin{aligned}
\int \tan x d x & =\int \frac{\sin x}{\cos x} d x=\int \frac{-d u}{u} & \begin{array}{l}
u=\cos x>0 \text { on }(-\pi / 2, \pi / 2), \
d u=-\sin x d x
\end{array} \
& =-\ln |u|+C=-\ln |\cos x|+C & \
& =\ln \frac{1}{|\cos x|}+C=\ln |\sec x|+C . & \text { Reciprocal Rule }
\end{aligned}
$$
对于cot,
$$
\begin{aligned}
\int \cot x d x & =\int \frac{\cos x d x}{\sin x}=\int \frac{d u}{u} \quad \begin{array}{l}
u=\sin x \
d u=\cos x d x
\end{array} \
& =\ln |u|+C=\ln |\sin x|+C=-\ln |\csc x|+C .
\end{aligned}
$$
要对$\sec x$积分,我们用1的代数形式乘除以$(\sec x+\tan x)$。
$$
\begin{aligned}
& \int \sec x d x=\int \sec x \frac{(\sec x+\tan x)}{(\sec x+\tan x)} d x=\int \frac{\sec ^2 x+\sec x \tan x}{\sec x+\tan x} d x \
& =\int \frac{d u}{u}=\ln |u|+C=\ln |\sec x+\tan x|+C \quad \begin{array}{ll}
u=\sec x+\tan x \
d u=\left(\sec x \tan x+\sec ^2 x\right) d x
\end{array}
\end{aligned}
$$
对于$\csc x$,我们乘以并除以$(\csc x+\cot x)$。
$$
\begin{aligned}
& \int \csc x d x=\int \csc x \frac{(\csc x+\cot x)}{(\csc x+\cot x)} d x=\int \frac{\csc ^2 x+\csc x \cot x}{\csc x+\cot x} d x \
& =\int \frac{-d u}{u}=-\ln |u|+C=-\ln |\csc x+\cot x|+C \quad u=\csc x+\cot x \
& d u=\left(-\csc x \cot x-\csc ^2 x\right) d x
\end{aligned}
$$
求正切,余切,正割和余割函数的积分
$$
\begin{array}{ll}
\int \tan u d u=\ln |\sec u|+C & \int \sec u d u=\ln |\sec u+\tan u|+C \
\int \cot u d u=\ln |\sin u|+C & \int \csc u d u=-\ln |\csc u+\cot u|+C
\end{array}
$$

数学代写|微积分代写Calculus代考 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。