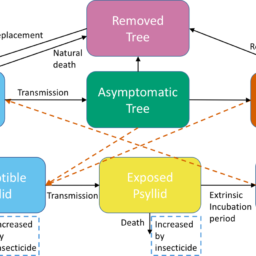
MY-ASSIGNMENTEXPERT™可以为您提供sydney MATH1013 Mathematical Modeling数学建模的代写代考和辅导服务!
这是悉尼大学数学建模课程的代写成功案例。

MATH1013课程简介
MATH1013 is designed for science students who do not intend to undertake higher year mathematics and statistics. In this unit of study students learn how to construct, interpret and solve simple differential equations and recurrence relations. Specific techniques include separation of variables, partial fractions and first and second order linear equations with constant coefficients. Students are also shown how to iteratively improve approximate numerical solutions to equations.
Prerequisites
At the completion of this unit, you should be able to:
- LO1. write down general and particular solutions to simple differential equations and recurrence relations describing models of growth and decay
- LO2. determine the order of a differential equation or recurrence relation
- LO3. find equilibrium solutions and analyse their stability using both graphical methods and slope conditions
- LO4. recognise and solve separable first-order differential equations
- LO5. use partial fractions and separation of variables to solve certain nonlinear differential equations, including the logistic equation
- LO6. use a variety of graphical and numerical techniques to locate and count solutions to equations
- LO7. solve equations numerically by fixed-point iteration, including checking if an iteration method is stable
- LO8. explore sequences numerically, and classify their long-term behaviour
- LO9. determine the general solution to linear second-order equations or simultaneous pairs of first order equations with constant coefficients.
MATH1013 Mathematical Modeling HELP(EXAM HELP, ONLINE TUTOR)
Suppose you’ve never heard of Archimedes, but you’ve experimented with various fluids and objects, and ascertained that whether an object floats or sinks depends on its weight, and on the fluid. You’ve also observed that whereas your stainless steel measuring cup floats nicely in the dish water, a steel ball bearing of the same mass sinks, so buoyancy must also depend on how much fluid is displaced. You thus conjecture that the buoyant force $B$ depends on the object’s mass $m$, the volume $V$ of fluid displaced, the density $\rho$ of the fluid, and gravitational acceleration $g$.
a. Explain why the gravitational acceleration should be included.
b. Form the dimensional matrix $\mathcal{D}$ of the five physical quantities $B, m, V, \rho$, and $g$.
c. Use dimensional analysis and the $\mathrm{Pi}$ Theorem to show that $B=\operatorname{V\rho g} f\left(\frac{\mathrm{m}}{\rho V}\right)$.
d. What does Archimedes’ Law of Buoyancy (see Example 2.2.3 in your lectures) tell you about the function $f$ ?
In 1862, William Thompson (a.k.a. Lord Kelvin) proposed that the age $t^*$ of the Earth depended on four quantities:
the temperature $u_0$ of the Earth’s crust at depth $y$ at the time $t=0$ when the Earth’s crust solidified;
the surface temperature $u_s$ of the Earth’s crust (which he assumed to be constant);
the thermal conductivity $\kappa$ of the rock $\left([\kappa]=\mathcal{L}^2 \mathcal{T}^{-1}\right)$; and
the gradient $u_y=\frac{\partial u}{\partial y}$ of the crust temperature near the surface.
a. Form the dimensional matrix $\mathcal{D}$ of the physical quantities $t^*, u_0, u_s, \kappa$, and $u_y$.
b. Use dimensional analysis and the Pi Theorem to show that $t^=\frac{u_s^2}{\kappa u_y^2} f\left(\frac{u_0}{u_s}\right)$ c. Lord Kelvin actually solved some nasty DEs to prove that, under his assumptions, $t^=\frac{\left(u_0-u_s\right)^2}{\pi \kappa u_y^2}$. If correct, what does this imply about the function $f\left(\frac{u_0}{u_s}\right)$ ?
Comment: Thompson estimated the age of the Earth to be about 98 million years, with a range of 20 to 400 million years. Once the effect of radioactivity in igneous rocks was discovered, his error in using a heat conduction model was corrected.
In a spacecraft, objects are essentially free of the force of gravity. Thus it seems reasonable to assume that the drag force $f_d$ on a smooth object of cross sectional area $A$ depends only on the density $\rho$ of the air inside the craft, the speed $v$ of the object, and $A$.
a. Form the dimensional matrix for the four physical quantities $f_d, A, \rho$, and $v$.
b. Apply dimensional analysis to show that $f_d$ is proportional to $\rho A v^2$.
c. Two astronauts are playing catch with a toy football in an orbiting spacecraft. One throws a spiral pass at speed $v_1$, presenting cross sectional area $A_1=\pi b c$. The other returns the ball with a sideways lob at speed $v_2=\frac{1}{2} v_1$, presenting cross sectional area $A_2=\pi a b$. If $a=10 \mathrm{~cm}$ and $c=5 \mathrm{~cm}$, what is the ratio of $f_{d_1}$ to $f_{d_2}$ ?
Review Example 4 (pages 59-61 of Edition 2, or 63-65 of Edition 1 of your text) which discussed escape velocity, i.e., the necessary initial velocity an object needs to escape the Earth’s gravitational field.
a. Form the dimensional matrix for the four physical quantities, the mass $m$ of the object, the Earth’s radius $R$, the gravitational acceleration $g$, and the escape velocity $v_e$.
b. Show that dimensional analysis gives the escape velocity correctly, up to a dimensionless constant $C$.
c. Suppose Planet X has radius 10 times that of Earth, and gravitational acceleration 2.5 times Earth’s. How does the escape velocity for Planet X compare to that for Earth?
Do problem 7 i. OR 7 ii, plus one of 8 or 9 , and one of 10 or 11 Phase Portrait Sketches (Do only one of 7 i. OR 7 ii)
MY-ASSIGNMENTEXPERT™可以为您提供SYDNEY MATH1013 MATHEMATICAL MODELING数学建模的代写代考和辅导服务!