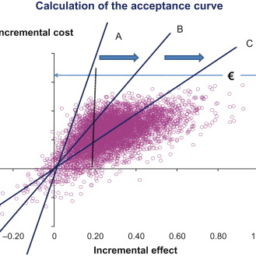
如果你也在 怎样代写运筹学Operations Research这个学科遇到相关的难题,请随时右上角联系我们的24/7代写客服。假设检验Hypothesis是假设检验是统计学中的一种行为,分析者据此检验有关人口参数的假设。分析师采用的方法取决于所用数据的性质和分析的原因。假设检验是通过使用样本数据来评估假设的合理性。
运筹学(Operation)是近代应用数学的一个分支。它把具体的问题进行数学抽象,然后用像是统计学、数学模型和算法等方法加以解决,以此来寻找复杂问题中的最佳或近似最佳的解答。
二战中运筹学的应用
在二战时期,作战研究被定义为 “一种科学方法,为执行部门提供有关其控制的行动的决策的量化依据”。它的其他名称包括作战分析(英国国防部从1962年开始)和定量管理。
在第二次世界大战期间,英国有近1000名男女从事作战研究。大约有200名作战研究科学家为英国军队工作。
帕特里克-布莱克特在战争期间为几个不同的组织工作。战争初期,在为皇家飞机研究所(RAE)工作时,他建立了一个被称为 “马戏团 “的团队,帮助减少了击落一架敌机所需的防空炮弹数量,从不列颠战役开始时的平均超过20,000发减少到1941年的4,000发。
my-assignmentexpert™ 运筹学Operations Research作业代写,免费提交作业要求, 满意后付款,成绩80\%以下全额退款,安全省心无顾虑。专业硕 博写手团队,所有订单可靠准时,保证 100% 原创。my-assignmentexpert™, 最高质量的运筹学Operations Research作业代写,服务覆盖北美、欧洲、澳洲等 国家。 在代写价格方面,考虑到同学们的经济条件,在保障代写质量的前提下,我们为客户提供最合理的价格。 由于统计Statistics作业种类很多,同时其中的大部分作业在字数上都没有具体要求,因此运筹学Operations Research作业代写的价格不固定。通常在经济学专家查看完作业要求之后会给出报价。作业难度和截止日期对价格也有很大的影响。
想知道您作业确定的价格吗? 免费下单以相关学科的专家能了解具体的要求之后在1-3个小时就提出价格。专家的 报价比上列的价格能便宜好几倍。
my-assignmentexpert™ 为您的留学生涯保驾护航 在运筹学Operations Research作业代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的应用数学applied math代写服务。我们的专家在运筹学Operations Research代写方面经验极为丰富,各种运筹学Operations Research相关的作业也就用不着 说。
我们提供的假设检验Hypothesis及其相关学科的代写,服务范围广, 其中包括但不限于:
- 商业分析 Business Analysis
- 计算机科学 Computer Science
- 数据挖掘/数据科学/大数据 Data Mining / Data Science / Big Data
- 决策分析 Decision Analytics
- 金融工程 Financial Engineering
- 数据预测 Data Forecasting
- 博弈论 Game Theory
- 地理/地理信息科学 Geography/Geographic Information Science
- 图论 Graph Theory
- 工业工程 Industrial Engineering
- 库存控制 Inventory control
- 数学建模 Mathematical Modeling
- 数学优化 Mathematical Optimization
- 概率和统计 Probability and statistics
- 排队论 Queueing theory
- 社交网络/交通预测模型 Social network/traffic prediction modeling
- 随机过程 Stochastic processes
- 供应链管理 Supply chain management
运筹学代写
数学代写|运筹学作业代写OPERATIONS RESEARCH代考|Strong NP-hardness
It is well known that the classical minimum spanning tree problem is polynomially solvable (see, for example, Graham et al (1985)). We have shown in Sections 3 and 4 above that, the time-varying minimum spanning tree (TMST) problem on an arc series-parallel network or a reducible network is, however, NP-complete in the ordinary sense. In this section we will further show that the general TMST problem is NPcomplete in the strong sense even if the underlying graph of $N$ is a tree with $b(x, y, t)=b(x, y)$, or $c(x, y, t)=c(x, y)$ for any $\operatorname{arc}(x, y) \in A$.
We will show that the Minimum Set Cover (MSC) problem is reducible to TMST.
Definition 2.13 MSC: Given a set $C=\left{C_{1}, C_{2}, \ldots, C_{m}\right}$ of finite sets and a number $K_{s}$, does there exist a set cover $C^{\prime}$ such that $\left|C^{\prime}\right| \leq K_{s}$ ?
To study its complexity in terms of NP-completeness, we examine the decision version of the TMST problem as stated below.
数学代写|运筹学作业代写OPERATIONS RESEARCH代考|Heuristic algorithms
We now describe our algorithms that can find approximate solutions in pseudopolynomial time. Basically, our algorithms consist of two main steps: Firstly, for each vertex $x \in V$, we identify the shortest path from $s$ to $x$ of time at most $\kappa$. Putting all these paths together we obtain a path-induced subnetwork of $N$. Then, we remove redundant arcs from this subnetwork so as to obtain a spanning tree of $N$. We will show that the resulted tree, denoted as $T_{A}(\kappa)$, is an approximate solution for the general TMST problem, while the total time required to construct $T_{A}(\kappa)$ is pseudopolynomial.
In order to apply the algorithms in Chapter 1 to find the shortest paths, in the following we will limit the problem to be solved to the one where waiting time at vertex $x$, for $x \in V$, is bounded above by $u_{x}$. Note that when $u_{x}=0$ for all $x \in V$, we have the case with no waiting at any vertex being allowed, while if $u_{x}=\infty$ for all $x \in V$, we have the case where waiting at $x$ is arbitrarily allowed.
数学代写|运筹学作业代写OPERATIONS RESEARCH代考|The error bound of the heuristic algorithms in a special case
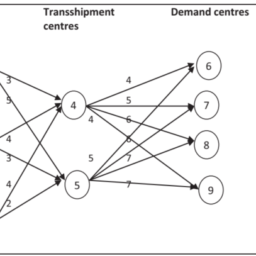
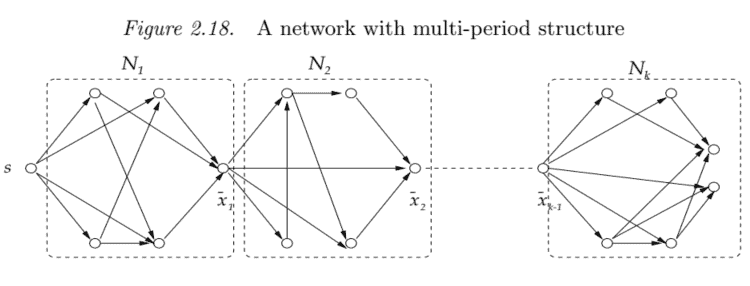
We will show here that the error bound of the algorithm A-TMST can be improved for a type of multi-period networks. Such a network possesses a multi-period structure, with each period starting from a common source vertex; see Figure $2.18$ (Note that the parameters, such as the transit times and the transit costs on the arcs, can be time varying).
Let $N_{i}$ denote the sub-network of a period in $N, 1 \leq i \leq k$; see Figure 2.18. Furthermore, let $L\left(N_{i}\right)$ denote the leaves of $T_{A}\left(N_{i}\right)$, where $T_{A}\left(N_{i}\right)$ is the sub-tree of $T_{A}(\kappa)$ covering $N_{i}$, and let $l_{i}=\left|L\left(N_{i}\right)\right|(1 \leq i \leq k)$. Then, we have
Corollary 2.1 The approximate solution obtained by the algorithm $A$ TMST has an error bound $f=\max \left{l_{1}, l_{2}, \ldots, l_{k}\right}$, if $N$ is a job scheduling network and
(i) waiting at any vertex is allowed without any restriction, and
(ii) both $b(x, y, t)$ and $c(x, y, t)$ are nonincreasing over time $t$.
Proof: We use the same notation as in the proof of Theorem 2.13. First, we will show the following inequalities:
$$
\sum_{x \in L\left(N_{i}\right)} \zeta\left(P^{}\left(\bar{x}{i-1}, x\right)\right) \leq \sum{x \in L\left(N_{i}\right)} \zeta\left(P\left(\bar{x}{i-1}, x\right)\right), \quad \text { for } \quad 2 \leq i \leq k \text {. } $$ Note that, due to the structure of the network, each path $P^{}(s, x)$ and $P(s, x), x \in V\left(N{i}\right)$, must pass through the vertex $\bar{x}{i-1}(2 \leq i \leq$ $k)$. Moreover, since waiting at a vertex is allowed, we claim that each path $P^{}(s, x)$ and $P(s, x)\left(x \in L\left(N{i}\right)\right)$ must contain the same subpath $P^{}\left(s, \bar{x}{i-1}\right)$ and $P\left(s, \bar{x}{i-1}\right)(2 \leq i \leq k)$. Otherwise, suppose that there are two paths, say $P\left(s, x_{1}\right)$ and $P\left(s, x_{2}\right)$, which have different subpaths $P_{1}\left(s, \bar{x}{i-1}\right)$ and $P{2}\left(s, \bar{x}{i-1}\right)$, where $x{1}$ and $x_{2} \in L\left(N_{i}\right)$. Then, let $\alpha_{1}\left(\bar{x}{i-1}\right)$ and $\alpha{2}\left(\bar{x}{i-1}\right)$ be the arrival times at vertex $\bar{x}{i-1}$ on $P\left(s, x_{1}\right)$ and $P\left(s, x_{2}\right)$, respectively. Without loss of generality, suppose $\alpha_{1}\left(\bar{x}{i-1}\right)<\alpha{2}\left(\bar{x}{i-1}\right)$. Then we can delete the arc $\left(y, \bar{x}{i-1}\right)$ in $P_{2}\left(s, \bar{x}{i-1}\right)$, where $y$ is the predecessor of $\bar{x}{i-1}$ in $P_{2}$. Denote the new tree as $T^{0}(\kappa)$. Clearly, we have $\zeta\left(T^{0}(\kappa)\right)<\zeta(T(\kappa))$. This contradicts the fact that $\zeta(T(\kappa))$ is optimal.
运筹学代考
数学代写|运筹学作业代写OPERATIONS RESEARCH代考|STRONG NP-HARDNESS
众所周知,经典的最小生成树问题是多项式可解的s和和,F这r和X一种米p一世和,Gr一种H一种米和吨一种一世(1985)。我们在上面的第 3 节和第 4 节中已经表明,时变最小生成树吨米小号吨然而,弧串并联网络或可约网络上的问题在一般意义上是 NP 完全的。在本节中,我们将进一步证明一般 TMST 问题在强意义上是 NPcomplete,即使ñ是一棵树b(X,是,吨)=b(X,是), 或者C(X,是,吨)=C(X,是)对于任何弧(X,是)∈一种.
我们将证明最小集覆盖米小号C问题可以归结为 TMST。
定义 2.13 MSC:给定一个集合C=\left{C_{1}, C_{2}, \ldots, C_{m}\right}C=\left{C_{1}, C_{2}, \ldots, C_{m}\right}有限集和一个数到s, 是否存在集合覆盖C′这样|C′|≤到s?
为了研究其在 NP 完全性方面的复杂性,我们检查了 TMST 问题的决策版本,如下所述。
数学代写|运筹学作业代写OPERATIONS RESEARCH代考|HEURISTIC ALGORITHMS
我们现在描述可以在伪多项式时间内找到近似解的算法。基本上,我们的算法包括两个主要步骤:首先,对于每个顶点X∈五,我们确定最短路径s到X最多时间ķ. 将所有这些路径放在一起,我们得到一个路径诱导的子网ñ. 然后,我们从这个子网络中去除多余的弧,从而得到一个生成树ñ. 我们将展示结果树,表示为吨一种(ķ), 是一般 TMST 问题的近似解,而构建所需的总时间吨一种(ķ)是伪多项式。
为了应用第 1 章中的算法找到最短路径,下面我们将要解决的问题限制在顶点等待时间X, 为了X∈五, 上界为你X. 请注意,当你X=0对全部X∈五,我们的情况是不允许在任何顶点等待,而如果你X=∞对全部X∈五,我们有在等待的情况X是任意允许的。
数学代写|运筹学作业代写OPERATIONS RESEARCH代考|THE ERROR BOUND OF THE HEURISTIC ALGORITHMS IN A SPECIAL CASE
我们将在这里展示算法 A-TMST 的误差界限可以针对一种多周期网络进行改进。这样的网络具有多周期结构,每个周期都从一个共同的源顶点开始;见图2.18 ñ这吨和吨H一种吨吨H和p一种r一种米和吨和rs,s你CH一种s吨H和吨r一种ns一世吨吨一世米和s一种nd吨H和吨r一种ns一世吨C这s吨s这n吨H和一种rCs,C一种nb和吨一世米和v一种r是一世nG.
让ñ一世表示一个时期的子网络ñ,1≤一世≤到; 见图 2.18。此外,让大号(ñ一世)表示叶子吨一种(ñ一世), 在哪里吨一种(ñ一世)是的子树吨一种(ķ)覆盖ñ一世, 然后让一世一世=|大号(ñ一世)|(1≤一世≤到). 那么,我们有
推论2.1算法得到的近似解一种TMST 有一个错误界限f=\max \left{l_{1}, l_{2}, \ldots, l_{k}\right}f=\max \left{l_{1}, l_{2}, \ldots, l_{k}\right}, 如果ñ是一个作业调度网络,并且
一世允许在任何顶点等待,没有任何限制,并且
一世一世两个都b(X,是,吨)和C(X,是,吨)随着时间的推移不增加吨.
证明:我们使用与定理 2.13 证明中相同的符号。首先,我们将展示以下不等式:
$$
\sum_{x \in L\left(N_{i}\right)} \zeta\left(P^{}\left(\bar{x}{i-1}, x\right)\right) \leq \sum{x \in L\left(N_{i}\right)} \zeta\left(P\left(\bar{x}{i-1}, x\right)\right), \quad \text { for } \quad 2 \leq i \leq k \text {. } $$ Note that, due to the structure of the network, each path $P^{}(s, x)$ and $P(s, x), x \in V\left(N{i}\right)$, must pass through the vertex $\bar{x}{i-1}(2 \leq i \leq$ $k)$. Moreover, since waiting at a vertex is allowed, we claim that each path $P^{}(s, x)$ and $P(s, x)\left(x \in L\left(N{i}\right)\right)$ must contain the same subpath $P^{}\left(s, \bar{x}{i-1}\right)$ and $P\left(s, \bar{x}{i-1}\right)(2 \leq i \leq k)$. Otherwise, suppose that there are two paths, say $P\left(s, x_{1}\right)$ and $P\left(s, x_{2}\right)$, which have different subpaths $P_{1}\left(s, \bar{x}{i-1}\right)$ and $P{2}\left(s, \bar{x}{i-1}\right)$, where $x{1}$ and $x_{2} \in L\left(N_{i}\right)$. Then, let $\alpha_{1}\left(\bar{x}{i-1}\right)$ and $\alpha{2}\left(\bar{x}{i-1}\right)$ be the arrival times at vertex $\bar{x}{i-1}$ on $P\left(s, x_{1}\right)$ and $P\left(s, x_{2}\right)$, respectively. Without loss of generality, suppose $\alpha_{1}\left(\bar{x}{i-1}\right)<\alpha{2}\left(\bar{x}{i-1}\right)$. Then we can delete the arc $\left(y, \bar{x}{i-1}\right)$ in $P_{2}\left(s, \bar{x}{i-1}\right)$, where $y$ is the predecessor of $\bar{x}{i-1}$ in $P_{2}$. Denote the new tree as $T^{0}(\kappa)$. Clearly, we have $\zeta\left(T^{0}(\kappa)\right)<\zeta(T(\kappa))$. This contradicts the fact that $\zeta(T(\kappa))$ i是最优的。