数学代写|Robust approximation 凸优化代考
凸优化代写
6.4.1 Stochastic robust approximation
We consider an approximation problem with basic objective $|A x-b|$, but also wish to take into account some uncertainty or possible variation in the data matrix $A$. (The same ideas can be extended to handle the case where there is uncertainty in both $A$ and $b$.) In this section we consider some statistical models for the variation in $A$.
We assume that $A$ is a random variable taking values in $\mathbf{R}^{m \times n}$, with mean $\bar{A}$, so we can describe $A$ as
$A=\bar{A}+U$, where $U$ is a random matrix with zero mean. Here, the constant It is natural to use the expected value of $|A x-b|$ as the objective:
It is natural to use the expected value of $| A x-b$ $$ \text { minimize } \mathrm{E}|A x-b| $$
We refer to this problem as the stochastic robust approximation problem. It is always a convex optimization problem, but usually not tractable since in most cases it is very difficult to evaluate the objective or its derivatives.
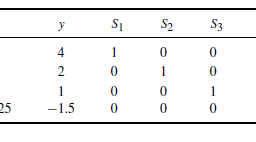
One simple case in which the stochastic robust approximation problem (6.13) can be solved occurs when $A$ assumes only a finite number of values, $i . e .$,
$$
\operatorname{prob}\left(A=A_{i}\right)=p_{i}, \quad i=1, \ldots, k
$$
where $A_{i} \in \mathbf{R}^{m \times n}, 1^{T} p=1, p \succeq 0$. In this case the problem (6.13) has the form minimize $p_{1}\left|A_{1} x-b\right|+\cdots+p_{k}\left|A_{k} x-b\right|$,
which is often called a sum-of-norms problem. It can be expressed as
$$
\begin{array}{ll}
\text { minimize } & p^{T} t \
\text { subject to } & \left|A_{i} x-b\right| \leq t_{i}, \quad i=1, \ldots, k
\end{array}
$$
where the variables are $x \in \mathbf{R}^{n}$ and $t \in \mathbf{R}^{k}$. If the norm is the Euclidean norm, this sum-of-norms problem is an SOCP. If the norm is the $\ell_{1}-$ or $\ell_{\infty}-$ norm, the sum-of-norms problem can be expressed as an LP; see exercise $6.8 .$
Some variations on the stochastic robust approximation problem (6.13) are tractable. As an example, consider the stochastic robust least-squares problem
minimize $\mathbf{E}|A x-b|_{2}^{2}$
where the norm is the Euclidean norm. We can express the objective as
$$
\begin{aligned}
\mathbf{E}|A x-b|_{2}^{2} &=\mathbf{E}(\bar{A} x-b+U x)^{T}(\bar{A} x-b+U x) \
&=(\bar{A} x-b)^{T}(\bar{A} x-b)+\mathbf{E} x^{T} U^{T} U x \
&=|\bar{A} x-b|_{2}^{2}+x^{T} P x
\end{aligned}
$$
319
where $P=\mathbf{E} U^{T} U$. Therefore the stochastic robust approximation problem has
the form of a regularized least-squares problem
with solution
$$
x=\left(\bar{A}^{T} \bar{A}+P\right)^{-1} \bar{A}^{T} b .
$$
This makes perfect sense: when the matrix $A$ is subject to variation, the vector $A x$ will have more variation the larger $x$ is, and Jensen’s inequality tells us that variation in $A x$ will increase the average value of $|A x-b|_{2}$. So we need to balance making $\bar{A} x-b$ small with the desire for a small $x$ (to keep the variation in $A x$ small), which is the essential idea of regularization.
This observation gives us another interpretation of the Tikhonov regularized least-squares problem $(6.10)$, as a robust least-squares problem, taking into account possible variation in the matrix $A$. The solution of the Tikhonov regularized least- squares problem $(6.10)$ minimizes $\mathbf{E}|(A+U) x-b|^{2}$, where $U_{i j}$ are zero mean, uncorrelated random variables, with variance $\delta / m$ (and here, $A$ is deterministic).
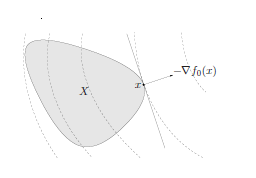
Worst-case robust approximation
It is also possible to model the variation in the matrix $A$ using a set-based, worstcase approach. We describe the uncertainty by a set of possible values for $A$ :
$$
A \in \mathcal{A} \subseteq \mathbf{R}^{m \times n},
$$
which we assume is nonempty and bounded. We define the associated worst-case error of a candidate approximate solution $x \in \mathbf{R}^{n}$ as
凸优化代考
6.4.1 随机稳健近似
我们考虑基本目标 $|A x-b|$ 的近似问题,但也希望考虑数据矩阵 $A$ 中的一些不确定性或可能的变化。 (同样的想法可以扩展到处理 $A$ 和 $b$ 都存在不确定性的情况。)在本节中,我们考虑一些用于 $A$ 变化的统计模型。
我们假设 $A$ 是一个随机变量,取值为 $\mathbf{R}^{m \times n}$,平均值为 $\bar{A}$,因此我们可以将 $A$ 描述为
$A=\bar{A}+U$,其中 $U$ 是一个均值为零的随机矩阵。这里,常数很自然地以$|A x-b|$的期望值作为目标:
使用 $| 的期望值是很自然的A x-b$ $$ \text { 最小化 } \mathrm{E}|A x-b| $$
我们将此问题称为随机稳健逼近问题。它始终是一个凸优化问题,但通常难以处理,因为在大多数情况下,很难评估目标或其衍生物。
当 $A$ 仅假设有限数量的值 $i 时,可以解决随机稳健近似问题 (6.13) 的一个简单情况。 e.$,
$$
\operatorname{prob}\left(A=A_{i}\right)=p_{i}, \quad i=1, \ldots, k
$$
其中 $A_{i} \in \mathbf{R}^{m \times n}, 1^{T} p=1, p \succeq 0$。在这种情况下,问题 (6.13) 的形式为最小化 $p_{1}\left|A_{1} xb\right|+\cdots+p_{k}\left|A_{k} xb\right\ |$,
这通常被称为范数和问题。它可以表示为
$$
\开始{数组}{ll}
\text { 最小化 } & p^{T} t \
\text { 服从 } & \left|A_{i} x-b\right| \leq t_{i}, \quad i=1, \ldots, k
\结束{数组}
$$
其中变量是 $x \in \mathbf{R}^{n}$ 和 $t \in \mathbf{R}^{k}$。如果范数是欧几里得范数,那么这个范数和问题就是 SOCP。如果范数是 $\ell_{1}-$ 或 $\ell_{\infty}-$ 范数,则范数和问题可以表示为 LP;见练习 $6.8 .$
随机稳健近似问题(6.13)的一些变体是易于处理的。例如,考虑随机稳健最小二乘问题
最小化 $\mathbf{E}|A x-b|_{2}^{2}$
其中范数是欧几里得范数。我们可以将目标表示为
$$
\开始{对齐}
\mathbf{E}|A xb|_{2}^{2} &=\mathbf{E}(\bar{A} x-b+U x)^{T}(\bar{A} x -b+U x) \
&=(\bar{A} x-b)^{T}(\bar{A} x-b)+\mathbf{E} x^{T} U^{T} U x \
&=|\bar{A} x-b|_{2}^{2}+x^{T} P x
\end{对齐}
$$
319
其中 $P=\mathbf{E} U^{T} U$。因此,随机鲁棒逼近问题有
正则化最小二乘问题的形式
有溶液
$$
x=\left(\bar{A}^{T} \bar{A}+P\right)^{-1} \bar{A}^{T} b 。
$$
这很有意义:当矩阵 $A$ 发生变化时,向量 $A x$ 的变化越大,$x$ 越大,Jensen 不等式告诉我们,$A x$ 的变化会增加平均值$|A xb|_{2}$。所以我们需要平衡使$\bar{A} x-b$ 变小和希望$x$ 变小(以保持$A x$ 的变化很小),这是正则化的基本思想。
这一观察为我们提供了对 Tikhonov 正则化最小二乘问题 $(6.10)$ 的另一种解释,它是一个稳健的最小二乘问题,同时考虑了矩阵 $A$ 的可能变化。 Tikhonov 正则化最小二乘问题 $(6.10)$ 的解使 $\mathbf{E}|(A+U) xb|^{2}$ 最小化,其中 $U_{ij}$ 为零均值,不相关随机变量,方差 $\delta / m$(这里,$A$ 是确定性的)。
最坏情况稳健近似
也可以使用基于集合的最坏情况方法对矩阵 $A$ 中的变化进行建模。我们通过 $A$ 的一组可能值来描述不确定性:
$$
A \in \mathcal{A} \subseteq \mathbf{R}^{m \times n},
$$
我们假设它是非空的和有界的。我们将候选近似解 $x \in \mathbf{R}^{n}$ 的相关最坏情况误差定义为

数学代写| Chebyshev polynomials 数值分析代考 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。
时间序列分析代写
统计作业代写
随机过程代写
随机过程,是依赖于参数的一组随机变量的全体,参数通常是时间。 随机变量是随机现象的数量表现,其取值随着偶然因素的影响而改变。 例如,某商店在从时间t0到时间tK这段时间内接待顾客的人数,就是依赖于时间t的一组随机变量,即随机过程