数学代写| Convex optimization problems in standard form 数值分析代考
数值分析代写
A convex optimization problem is one of the form
$$
\begin{array}{ll}
\text { minimize } & f_{0}(x) \
\text { subject to } & f_{1}(x) \leq 0, \quad i=1, \ldots, m \
& a_{i}^{T} x=b_{i}, \quad i=1, \ldots, p
\end{array}
$$
where $f_{0}, \ldots, f_{\mathrm{m}}$ are convex functions. Comparing (4.15) with the general standard form problem (4.1), the convex problem has three additional requirements:
137
- the objective function must be convex,
- the inequality constraint functions must be convex,
- the equality constraint functions $h_{\mathrm{a}}(x)=a_{i}^{T} x-b_{\mathrm{r}}$ must be affine.
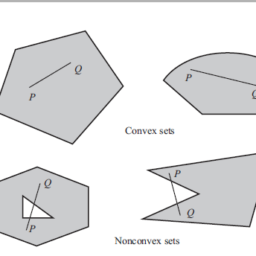
We immediately note an important property: The feasible set of a convex optimization problem is convex, since it is the intersection of the domain of the problem
$$
\mathcal{D}=\bigcap_{i=0}^{m} \operatorname{dom} f_{i}
$$
which is a convex set, with $m$ (convex) sublevel sets $\left{x \mid f_{1}(x) \leq 0\right}$ and $p$ hyperplanes $\left{x \mid a_{i}^{T} x=b_{i}\right}$. (We can assume without loss of generality that $a_{1} \neq 0$ : if $a_{1}=0$ and $b_{i}=0$ for some $i$, then the $i$ th equality constraint can be deleted; if $a_{1}=0$ and $b_{1} \neq 0$, the $i$ th equality constraint is inconsistent, and the problem is infeasible.) Thus, in a convex optimization problem, we minimize a convex objective function over a convex set.
If $f_{0}$ is quasiconvex instead of convex, we say the problem (4.15) is a (standard form) quasiconvex optimization problem. Since the sublevel sets of a convex or quasiconvex function are convex, we conclude that for a convex or quasiconvex optimization problem the $\epsilon$-suboptimal sets are convex. In particular, the optimal set is convex. If the objective is strictly convex, then the optimal set contains at most one point.
Concave maximization problems
With a slight abuse of notation, we will also refer toConcave maximization problems
With a slight abuse of notation, we will also refer to
$$
\begin{array}{ll}
\text { maximize } & f_{0}(x) \
\text { subject to } & f_{1}(x) \leq 0, \quad i=1, \ldots, m \
& a_{i}^{T} x=b_{i}, \quad i=1, \ldots, p,
\end{array}
$$
as a convex optimization problem if the objective function $f_{0}$ is concave, and the inequality constraint functions $f_{1}, \ldots, f_{m}$ are convex. This concave maximization problem is readily solved by minimizing the convex objective function $-f_{0}$. All of the results, conclusions, and algorithms that we describe for the minimization problem are easily transposed to the maximization case. In a similar way the maximization problem (4.16) is called quasiconvex if $f_{0}$ is quasiconcave.
Abstract form convex optimization problem
It is important to note a subtlety in our definition of convex optimization problem. Consider the example with $x \in \mathbf{R}^{2}$,
$$
\begin{array}{ll}
\text { minimize } & f_{0}(x)=x_{1}^{2}+x_{2}^{2} \
\text { subject to } & f_{1}(x)=x_{1} /\left(1+x_{2}^{2}\right) \leq 0 \
& h_{1}(x)=\left(x_{1}+x_{2}\right)^{2}=0
\end{array}
$$
which is in the standard form (4.1). This problem is not a convex optimization problem in standard form since the equality constraint function $h_{1}$ is not affine, and
4 Convex optimization problems
138
数值分析代考
凸优化问题是其中一种形式
$$
\开始{数组}{ll}
\text { 最小化 } & f_{0}(x) \
\text { 服从 } & f_{1}(x) \leq 0, \quad i=1, \ldots, m \
& a_{i}^{T} x=b_{i}, \quad i=1, \ldots, p
\结束{数组}
$$
其中 $f_{0}, \ldots, f_{\mathrm{m}}$ 是凸函数。比较(4.15)和一般标准形式问题(4.1),凸问题有三个额外的要求:
137
- 目标函数必须是凸的,
- 不等式约束函数必须是凸的,
- 等式约束函数 $h_{\mathrm{a}}(x)=a_{i}^{T} x-b_{\mathrm{r}}$ 必须是仿射的。
我们立即注意到一个重要性质:凸优化问题的可行集是凸的,因为它是问题域的交集
$$
\mathcal{D}=\bigcap_{i=0}^{m} \operatorname{dom} f_{i}
$$
这是一个凸集,具有 $m$ (convex) 子集 $\left{x \mid f_{1}(x) \leq 0\right}$ 和 $p$ 超平面 $\left{x \中间 a_{i}^{T} x=b_{i}\right}$。 (我们可以不失一般性地假设 $a_{1} \neq 0$ :如果 $a_{1}=0$ 和 $b_{i}=0$ 对于某些 $i$,那么第 $i$ 等式约束可以删除;如果$a_{1}=0$且$b_{1} \neq 0$,则第$i$个等式约束不一致,问题不可行。)因此,在凸优化问题中,我们最小化凸集上的凸目标函数。
如果 $f_{0}$ 是拟凸的而不是凸的,我们说问题 (4.15) 是一个(标准形式的)拟凸优化问题。由于凸或拟凸函数的子级集是凸的,因此我们得出结论,对于凸或拟凸优化问题,$\epsilon$-次优集是凸的。特别是,最优集是凸的。如果目标是严格凸的,那么最优集最多包含一个点。
凹面最大化问题
稍微滥用符号,我们也会参考凹最大化问题
稍微滥用符号,我们还将参考
$$
\开始{数组}{ll}
\text { 最大化 } & f_{0}(x) \
\text { 服从 } & f_{1}(x) \leq 0, \quad i=1, \ldots, m \
& a_{i}^{T} x=b_{i}, \quad i=1, \ldots, p,
\结束{数组}
$$
如果目标函数 $f_{0}$ 是凹的,并且不等式约束函数 $f_{1}, \ldots, f_{m}$ 是凸的,则作为凸优化问题。这个凹最大化问题很容易通过最小化凸目标函数 $-f_{0}$ 来解决。我们为最小化问题描述的所有结果、结论和算法都可以很容易地转换为最大化情况。以类似的方式,如果 $f_{0}$ 是拟凹的,则最大化问题 (4.16) 称为拟凸。
抽象形式凸优化问题
重要的是要注意我们对凸优化问题的定义中的一个微妙之处。考虑 $x \in \mathbf{R}^{2}$ 的例子,
$$
\开始{数组}{ll}
\text { 最小化 } & f_{0}(x)=x_{1}^{2}+x_{2}^{2} \
\text { 服从 } & f_{1}(x)=x_{1} /\left(1+x_{2}^{2}\right) \leq 0 \
& h_{1}(x)=\left(x_{1}+x_{2}\right)^{2}=0
\结束{数组}
$$
这是标准形式(4.1)。这个问题不是标准形式的凸优化问题,因为等式约束函数 $h_{1}$ 不是仿射的,并且
4 凸优化问题
138

数学代写| Chebyshev polynomials 数值分析代考 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。
时间序列分析代写
统计作业代写
随机过程代写
随机过程,是依赖于参数的一组随机变量的全体,参数通常是时间。 随机变量是随机现象的数量表现,其取值随着偶然因素的影响而改变。 例如,某商店在从时间t0到时间tK这段时间内接待顾客的人数,就是依赖于时间t的一组随机变量,即随机过程