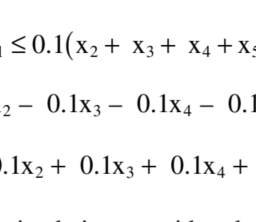如果你也在 怎样代写运筹学Operations Research这个学科遇到相关的难题,请随时右上角联系我们的24/7代写客服。假设检验Hypothesis是假设检验是统计学中的一种行为,分析者据此检验有关人口参数的假设。分析师采用的方法取决于所用数据的性质和分析的原因。假设检验是通过使用样本数据来评估假设的合理性。
运筹学(Operation)是近代应用数学的一个分支。它把具体的问题进行数学抽象,然后用像是统计学、数学模型和算法等方法加以解决,以此来寻找复杂问题中的最佳或近似最佳的解答。
二战中运筹学的应用
在二战时期,作战研究被定义为 “一种科学方法,为执行部门提供有关其控制的行动的决策的量化依据”。它的其他名称包括作战分析(英国国防部从1962年开始)和定量管理。
在第二次世界大战期间,英国有近1000名男女从事作战研究。大约有200名作战研究科学家为英国军队工作。
帕特里克-布莱克特在战争期间为几个不同的组织工作。战争初期,在为皇家飞机研究所(RAE)工作时,他建立了一个被称为 “马戏团 “的团队,帮助减少了击落一架敌机所需的防空炮弹数量,从不列颠战役开始时的平均超过20,000发减少到1941年的4,000发。
my-assignmentexpert™ 运筹学Operations Research作业代写,免费提交作业要求, 满意后付款,成绩80\%以下全额退款,安全省心无顾虑。专业硕 博写手团队,所有订单可靠准时,保证 100% 原创。my-assignmentexpert™, 最高质量的运筹学Operations Research作业代写,服务覆盖北美、欧洲、澳洲等 国家。 在代写价格方面,考虑到同学们的经济条件,在保障代写质量的前提下,我们为客户提供最合理的价格。 由于统计Statistics作业种类很多,同时其中的大部分作业在字数上都没有具体要求,因此运筹学Operations Research作业代写的价格不固定。通常在经济学专家查看完作业要求之后会给出报价。作业难度和截止日期对价格也有很大的影响。
想知道您作业确定的价格吗? 免费下单以相关学科的专家能了解具体的要求之后在1-3个小时就提出价格。专家的 报价比上列的价格能便宜好几倍。
my-assignmentexpert™ 为您的留学生涯保驾护航 在运筹学Operations Research作业代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的应用数学applied math代写服务。我们的专家在运筹学Operations Research代写方面经验极为丰富,各种运筹学Operations Research相关的作业也就用不着 说。
我们提供的假设检验Hypothesis及其相关学科的代写,服务范围广, 其中包括但不限于:
- 商业分析 Business Analysis
- 计算机科学 Computer Science
- 数据挖掘/数据科学/大数据 Data Mining / Data Science / Big Data
- 决策分析 Decision Analytics
- 金融工程 Financial Engineering
- 数据预测 Data Forecasting
- 博弈论 Game Theory
- 地理/地理信息科学 Geography/Geographic Information Science
- 图论 Graph Theory
- 工业工程 Industrial Engineering
- 库存控制 Inventory control
- 数学建模 Mathematical Modeling
- 数学优化 Mathematical Optimization
- 概率和统计 Probability and statistics
- 排队论 Queueing theory
- 社交网络/交通预测模型 Social network/traffic prediction modeling
- 随机过程 Stochastic processes
- 供应链管理 Supply chain management
运筹学代写
数学代写|运筹学作业代写OPERATIONS RESEARCH代考|FUNDAMENTAL NATURE OF SENSITIVITY ANALYSIS
To illustrate the nature of sensitivity analysis, the following two cases have been discussed.
Case 1: Section $2.5 .2$ explained an illustration regarding minimization of loss in revenue of a restaurant, which utilized two types of seating arrangements (A and B). The decision variables indicated the number of seats required of each type of arrangement notated by $\mathrm{x}{1}$ and $\mathrm{x}{2}$. Loss in revenue if one A type of seat goes vacant was $\$ 10$, whereas that of $\mathrm{B}$ was $\$ 15$ leading to formation of the objective function:
Minimize $\mathrm{Z}=10 \mathrm{x}{1}+15 \mathrm{x}{2}$
The final solution implied that value of decision variables $x_{1}$ and $x_{2}$ were 20 and 15 , respectively.
Now, according to the additivity assumption of LPP, as discussed in Section 2.3, every function in a LPP, whether it is an objective function or the right-hand side (RHS) of constrain function, is the sum of contribution of each individual activity. Thus, in this case, loss in revenue is sum of losses due to vacant seats of types A and B. To reduce such losses, the manager decided to use the same space for organizing small parties, mostly on weekdays when demand for restaurant services was less as compared to weekends. The promotion campaign led to more footfalls and down the line losses in revenue showed a downward trend due to increased occupancy. But the manager found that the decrease in loss in revenue was more than just because of higher occupancy of A and B types of seats. This was attributed to the utilization of the same restaurant space as a banquet hall for conduct of small-scale parties. Thus, both types of seating arrangements are complementary to each other in decreasing loss of revenue due to the capacity of the restaurant as well as that of the banquet hall.
Thus, in the case of complementary products, the objective function would be $10 \mathrm{x}{1}+15 \mathrm{x}{2}-\mathrm{x}{1} \mathrm{x}{2}$. In this case, parameter $\mathrm{x}{1} \mathrm{x}{2}$ has been subtracted as complimentary nature of items, resulting in decrease of loss in revenue. So, the value of $\mathrm{Z}$ when $\mathrm{x}{1}=20$ and $\mathrm{x}{2}=15$ would be $\mathrm{Z}=10 * 20+15 * 15-20^{} 15=125$ instead of $\mathrm{Z}=10^{} 20+15 * 15=425$.
Similarly, if two items are competitive, then also value of objective function would undergo a change. If demand for any or both of services increases, then they would be competing with each other for the same space at the same time. For instance, demand for parties increases on weekends. In addition to demand for restaurant, the manager has to decide which service to forego. Competition for the same facility between two services could result in an increase in loss of revenue. Thus, the objective function would be $\mathrm{Z}=10 \mathrm{x}{1}+15 \mathrm{x}{2}+\mathrm{x}{1} \mathrm{x}{2}$. So, the value of $\mathrm{Z}$ when $x_{1}=20$ and $x_{2}=15$ would be $\mathrm{Z}=10^{} 20+15^{} 15+20 * 15=725$ instead of $\mathrm{Z}=10^{} 20+15^{} 15=425$.
The above case indicates a change in value of an objective function with change in values of parameters indicating their sensitivity. This change can also be observed in the case of constraint functions where the additivity assumption of sum of individual contribution is characterized. For instance, the fourth constraint in the same case was that the maximum capacity of seats of both types was 40 . To illustrate, just for supposition purposes, if due to rush of customers, $50 \%$ more seats were added to the restaurant to make it more congested, then it would lead to increase in capacity. This would make the constraint as $1 \mathrm{x}{1}+1 \mathrm{x}{2}+0.5 \mathrm{x}{1} \mathrm{x}{2} \leq 40$. Putting the values of $\mathrm{x}{1}=20$ and $x{2}=15$ in the equation $1^{} 20+1^{} 15+0.5^{} 20^{} 15=185$ instead of 35 which was obtained from $1 \mathrm{x}{1}+1 \mathrm{x}{2} \leq 40$.
Therefore, the value of optimal solution is subject to change depending on the selection of parameter value. Thus, conduct of post-optimality analysis by using sensitivity analysis is of prime importance in finding feasible and optimal solution.
Case 2: Another illustration to emphasize the application of sensitivity analysis in determining sensitive parameters has been discussed here which involves a scenario wherein the proportionality assumption of LPP is violated. As discussed in Section 2.3, this assumption implies that the value of an objective function changes in proportion to the change in level of activity represented by decision variables. The same happens for constraint function where value of the left side of the function is proportional to the level of activity. For instance, a toy manufacturer involved in manufacturing of three types of dolls (A, B and C) earns a profit of $\$ 1, \$ 1.3$ and $\$ 1.1$ per unit, respectively. Then, if $\mathrm{x}{1}, \mathrm{x}{2}$ and $\mathrm{x}{3}$ are the number of dolls of $\mathrm{A}, \mathrm{B}$ and $\mathrm{C}$, then total profit would be $1 \mathrm{x}{1}+1.3 \mathrm{x}{2}+1.1 \mathrm{x}{3}$. Three decision variables represent the level of activity, implying that one unit of $x_{1}$ would generate profit of $\$ 1$, whereas its two units would earn profit of $\$ 2$. Thus, change is in proportion to change in level of activity.
But in certain scenarios, this proportionality assumption is violated. In most manufacturing processes, production involves certain set up costs which are incurred due to setting of machinery, raw material, tools, etc. Once the facilities are set up, then they can be utilized for production of the entire lot, and such costs are not incurred after production of each unit. Thus, it is one time cost. If set up cost for each type of doll i.e. from A to $\mathrm{B}$ is $\$ 0.1$, then profit from manufacturing of $\mathrm{A}$ is $1 \mathrm{x}{1}-0.1$ rather than $1 \mathrm{x}{1}$.
Another case could be that the profit function is enhanced not only by contribution from decision variable but due to economies of scale obtained from longer production runs, mass production system and offering of quantity discounts. Thus if A type of doll is produced in high volumes making the production process efficient, then profit instead of $1 x_{1}$ could be $1 x_{1}+y_{1}$ where $y_{1}$ is profit obtained due to economies of scale. Similarly, assumed extra profit due to mass production of $B$ and $C$ types of dolls would be $\mathrm{y}{2}$ and $\mathrm{y}{3}$. Hence, instead of profit being $1 \mathrm{x}{1}+1.3 \mathrm{x}{2}+1.1 \mathrm{x}{3}$ in the modelled problem, it would be $\left(1 x{1}+y_{2}\right)+\left(1.3 x_{2}+y_{3}\right)+\left(1.1 x_{3}+y_{3}\right)$ in real future scenario. This clearly violates the principle of proportionality.
Finally, the proportionality assumption might also be violated followed in constraint function. For instance, in above example of doll manufacturing, out of total production time of 440 minutes available, one unit of doll A and $\mathrm{C}$ takes $1.8$ minutes to manufacture, whereas one unit of doll B takes $2.7$ minutes. Thus, the constraint function of production time becomes $1.8 \mathrm{x}{1}+2.7 \mathrm{x}{2}+1.8 \mathrm{x}{3}$. Now, as both $\mathrm{A}$ and $\mathrm{C}$ takes same amount of time, so during the changeover from $\mathrm{A}$ to $\mathrm{B}$, the spare time for which machine is idle can be used to manufacture $C$. Thus, the production time of $C$ would be less than $1.8$ minutes. If utilized spare time was $0.8$ minutes for supposition purposes, then one unit of doll $\mathrm{C}$ is manufactured in $1.0$ minutes, making constraint function in reality as $1.8 \mathrm{x}{1}+2.7 \mathrm{x}{2}+1.0 \mathrm{x}{3}$.
These two cases involving different hypothesized examples make clear that parameters both in objective and constraint functions are estimates that are prone to change with changing circumstances. Another reason for their sensitivity could be that members of the OR team have not taken into account all the variables that go into estimating parameters. Hence it becomes increasingly important to conduct
sensitivity analysis for the proper evaluation of optimal solution as only then the solution could be considered as valid. The following section helps in interpreting the implications of sensitivity analysis when there is change in:
i. Right-hand side (RHS) value of constraint function;
ii. coefficients of basic variable in objective function; and
iii. coefficients of non-basic variable in objective function.
The following sections discuss both cases by first giving an example where a changed value in parameter value is shown to have an impact on the initial optimal solution. Second, the range of values of changed parameters over which solution would remain optimal is estimated. It is important to mention here that conditions of both feasibility and optimality need to be met at each step of the procedure. The feasibility of a solution is implied by non-negative RHS values of all basic variables in the simplex table. Whereas a solution is considered optimal if values in the net evaluation row are either zero or positive in case of minimization or zero or negative in case of maximization. More importantly, the values of all non-basic variables in $\mathrm{z}_{\mathrm{j}}$ row of the simplex table need to be non-negative to make a solution optimal.
运筹学代考
数学代写|运筹学作业代写OPERATIONS RESEARCH代考|FUNDAMENTAL NATURE OF SENSITIVITY ANALYSIS
为了说明敏感性分析的性质,我们讨论了以下两种情况。
案例1:部分2.5.2解释了一个关于最小化餐厅收入损失的插图,该餐厅使用了两种座位安排一种一种nd乙. 决策变量表示由 $\mathrm{x} {1}表示的每种安排所需的座位数一种nd\mathrm{x} {2}.一世○ss一世nr和v和n你和一世F○n和一种吨和p和○Fs和一种吨G○和sv一种C一种n吨在一种s$ 10,在H和r和一种s吨H一种吨○F\数学{B}在一种s$ 15一世和一种d一世nG吨○F○r米一种吨一世○n○F吨H和○bj和C吨一世v和F你nC吨一世○n:和\mathrm{Z}=10 \mathrm{x} {1}+15 \mathrm{x} {2}和sx_{1}一种ndx_{2}$ 分别为 20 和 15 。
现在,根据 LPP 的可加性假设,如第 2.3 节所述,LPP 中的每个函数,无论是目标函数还是右手边RH小号约束函数,是每个单独活动的贡献的总和。因此,在这种情况下,收入损失是 A 类和 B 类空位造成的损失之和。为了减少这种损失,经理决定使用相同的空间来组织小型聚会,主要是在餐厅服务需求不足的工作日。比周末少。促销活动导致更多客流量,由于入住率增加,收入损失呈下降趋势。但经理发现,收入损失的减少不仅仅是因为 A 和 B 类座位的占用率较高。这归因于利用与宴会厅相同的餐厅空间来举办小型聚会。因此,
因此,在互补产品的情况下,目标函数将是 $10 \mathrm{x} {1}+15 \mathrm{x} {2}-\mathrm{x} {1} \mathrm{x} {2}.一世n吨H一世sC一种s和,p一种r一种米和吨和r\mathrm{x} {1} \mathrm{x} {2}H一种sb和和ns你b吨r一种C吨和d一种sC○米p一世一世米和n吨一种r和n一种吨你r和○F一世吨和米s,r和s你一世吨一世nG一世nd和Cr和一种s和○F一世○ss一世nr和v和n你和.小号○,吨H和v一种一世你和○F\mathrm{Z}在H和n\mathrm{x} {1}=20一种nd\mathrm{x} {2}=15在○你一世db和\mathrm{Z}=10 * 20+15 * 15-20^{ } 15=125一世ns吨和一种d○F\mathrm{Z}=10^{ } 20+15 * 15=425$。
同样,如果两个项目具有竞争力,那么目标函数的值也会发生变化。如果对任何一项或两项服务的需求增加,那么它们将同时在同一空间相互竞争。例如,周末聚会的需求增加。除了对餐厅的需求外,经理还必须决定放弃哪些服务。两种服务之间对同一设施的竞争可能会导致收入损失的增加。因此,目标函数将是 $\mathrm{Z}=10 \mathrm{x} {1}+15 \mathrm{x} {2}+\mathrm{x} {1} \mathrm{x} {2}.小号○,吨H和v一种一世你和○F\mathrm{Z}在H和nx_{1}=20一种ndx_{2}=15在○你一世db和\mathrm{Z}=10^{ } 20+15^{ } 15+20 * 15=725一世ns吨和一种d○F\mathrm{Z}=10^{ } 20+15^{ } 15=425$。
上述情况表明了目标函数值的变化,参数值的变化表明了它们的敏感性。这种变化也可以在约束函数的情况下观察到,其中个体贡献之和的可加性假设被表征。例如,同一案例中的第四个约束条件是两种类型的座位的最大容量都是 40 。举例说明,只是为了假设的目的,如果由于客户的匆忙,50%餐厅增加了更多的座位,使其更加拥挤,然后会导致容量增加。这将使约束为 $1 \mathrm{x} {1}+1 \mathrm{x} {2}+0.5 \mathrm{x} {1} \mathrm{x} {2} \leq 40.磷你吨吨一世nG吨H和v一种一世你和s○F\mathrm{x} {1}=20一种ndx {2}=15一世n吨H和和q你一种吨一世○n1^{} 20+1^{} 15+0.5^{} 20^{} 15=185一世ns吨和一种d○F35在H一世CH在一种s○b吨一种一世n和dFr○米1 \mathrm{x} {1}+1 \mathrm{x} {2} \leq 40$。
因此,最优解的值会随着参数值的选择而变化。因此,使用敏感性分析进行后优化分析对于找到可行和最优的解决方案至关重要。
案例 2:此处讨论了另一个强调在确定敏感参数中应用敏感性分析的示例,其中涉及违反 LPP 的比例假设的场景。正如第 2.3 节所讨论的,这个假设意味着目标函数的值的变化与决策变量所代表的活动水平的变化成比例。约束函数也是如此,其中函数左侧的值与活动水平成正比。例如,一家玩具制造商涉及制造三种类型的玩偶一种,乙一种ndC赚取利润$1,$1.3和$1.1每单位,分别。那么,如果 $\mathrm{x} {1},\mathrm{x} {2}一种nd\mathrm{x} {3}一种r和吨H和n你米b和r○Fd○一世一世s○F\mathrm{A}, \mathrm{B}一种nd\mathrm{C},吨H和n吨○吨一种一世pr○F一 在○你一世db和1 \mathrm{x} {1}+1.3 \mathrm{x} {2}+1.1 \mathrm{x} {3}.吨Hr和和d和C一世s一世○nv一种r一世一种b一世和sr和pr和s和n吨吨H和一世和v和一世○F一种C吨一世v一世吨和,1×1 + 1.3×2 + 1.1×3. x_{1}在○你一世dG和n和r一种吨和pr○F一世吨○F$ 1,在H和r和一种s一世吨s吨在○你n一世吨s在○你一世d和一种rnpr○F一世吨○F2美元。因此,变化与活动水平的变化成比例。
但在某些情况下,违反了这种比例假设。在大多数制造过程中,生产涉及一定的设置成本,这些成本是由于机器、原材料、工具等的设置而产生的。一旦设备设置好,就可以用于整批的生产,这些成本是每个单元生产后不发生。因此,这是一次成本。如果为每种类型的娃娃设置成本,即从 A 到乙是$0.1,然后从制造中获利一种是 $1 \mathrm{x} {1}-0.1r一种吨H和r吨H一种n1 \mathrm{x} {1}$。
另一种情况可能是,利润函数不仅通过决策变量的贡献得到增强,而且由于从更长的生产运行、大规模生产系统和提供数量折扣中获得的规模经济。因此,如果大批量生产 A 型玩偶,使生产过程高效,那么利润而不是1X1可能1X1+和1在哪里和1是由于规模经济而获得的利润。同样,假设由于大规模生产的额外利润乙和C玩偶的类型是 $\mathrm{y} {2}一种nd\mathrm{y} {3}.H和nC和,一世ns吨和一种d○Fpr○F一世吨b和一世nG1 \mathrm{x} {1}+1.3 \mathrm{x} {2}+1.1 \mathrm{x} {3}一世n吨H和米○d和一世一世和dpr○b一世和米,一世吨在○你一世db和\left(1 x {1}+y_{2}\right)+\left1.3 x_{2}+y_{3}\右1.3 x_{2}+y_{3}\右+\左1.1 x_{3}+y_{3}\右1.1 x_{3}+y_{3}\右$ 在真实的未来场景中。这显然违反了比例原则。
最后,在约束函数中也可能违反比例假设。例如,在上面的娃娃制造示例中,在可用的 440 分钟的总生产时间中,一个单位的娃娃 A 和C需要1.8制造时间,而一个单位的娃娃 B 需要2.7分钟。因此,生产时间的约束函数变为 $1.8 \mathrm{x} {1}+2.7 \mathrm{x} {2}+1.8 \mathrm{x} 1.8×1 + 2.7×2 + 1.0×3.
这两个涉及不同假设示例的案例清楚地表明,目标函数和约束函数中的参数都是容易随环境变化而变化的估计值。他们敏感的另一个原因可能是 OR 团队的成员没有考虑到估计参数的所有变量。因此,如何进行变得越来越重要
用于正确评估最优解的敏感性分析,因为只有这样才能认为该解是有效的。以下部分有助于解释在以下方面发生变化时敏感性分析的含义:
i.右手边RH小号约束函数的值;
ii. 目标函数中基本变量的系数;iii
. 目标函数中非基本变量的系数。
以下部分通过首先给出一个示例来讨论这两种情况,其中显示参数值的变化值会对初始最优解产生影响。其次,估计解决方案将保持最佳的变化参数的值范围。在这里需要提到的是,在程序的每一步都需要满足可行性和最优性的条件。解决方案的可行性由单纯形表中所有基本变量的非负 RHS 值暗示。而如果净评估行中的值在最小化的情况下为零或正,或者在最大化的情况下为零或负,则认为解决方案是最优的。更重要的是,所有非基本变量的值和j单纯形表的行必须是非负的才能使解决方案最优。