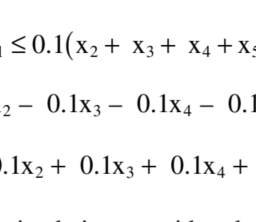如果你也在 怎样代写运筹学Operations Research这个学科遇到相关的难题,请随时右上角联系我们的24/7代写客服。假设检验Hypothesis是假设检验是统计学中的一种行为,分析者据此检验有关人口参数的假设。分析师采用的方法取决于所用数据的性质和分析的原因。假设检验是通过使用样本数据来评估假设的合理性。
运筹学(Operation)是近代应用数学的一个分支。它把具体的问题进行数学抽象,然后用像是统计学、数学模型和算法等方法加以解决,以此来寻找复杂问题中的最佳或近似最佳的解答。
二战中运筹学的应用
在二战时期,作战研究被定义为 “一种科学方法,为执行部门提供有关其控制的行动的决策的量化依据”。它的其他名称包括作战分析(英国国防部从1962年开始)和定量管理。
在第二次世界大战期间,英国有近1000名男女从事作战研究。大约有200名作战研究科学家为英国军队工作。
帕特里克-布莱克特在战争期间为几个不同的组织工作。战争初期,在为皇家飞机研究所(RAE)工作时,他建立了一个被称为 “马戏团 “的团队,帮助减少了击落一架敌机所需的防空炮弹数量,从不列颠战役开始时的平均超过20,000发减少到1941年的4,000发。
my-assignmentexpert™ 运筹学Operations Research作业代写,免费提交作业要求, 满意后付款,成绩80\%以下全额退款,安全省心无顾虑。专业硕 博写手团队,所有订单可靠准时,保证 100% 原创。my-assignmentexpert™, 最高质量的运筹学Operations Research作业代写,服务覆盖北美、欧洲、澳洲等 国家。 在代写价格方面,考虑到同学们的经济条件,在保障代写质量的前提下,我们为客户提供最合理的价格。 由于统计Statistics作业种类很多,同时其中的大部分作业在字数上都没有具体要求,因此运筹学Operations Research作业代写的价格不固定。通常在经济学专家查看完作业要求之后会给出报价。作业难度和截止日期对价格也有很大的影响。
想知道您作业确定的价格吗? 免费下单以相关学科的专家能了解具体的要求之后在1-3个小时就提出价格。专家的 报价比上列的价格能便宜好几倍。
my-assignmentexpert™ 为您的留学生涯保驾护航 在运筹学Operations Research作业代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的应用数学applied math代写服务。我们的专家在运筹学Operations Research代写方面经验极为丰富,各种运筹学Operations Research相关的作业也就用不着 说。
我们提供的假设检验Hypothesis及其相关学科的代写,服务范围广, 其中包括但不限于:
- 商业分析 Business Analysis
- 计算机科学 Computer Science
- 数据挖掘/数据科学/大数据 Data Mining / Data Science / Big Data
- 决策分析 Decision Analytics
- 金融工程 Financial Engineering
- 数据预测 Data Forecasting
- 博弈论 Game Theory
- 地理/地理信息科学 Geography/Geographic Information Science
- 图论 Graph Theory
- 工业工程 Industrial Engineering
- 库存控制 Inventory control
- 数学建模 Mathematical Modeling
- 数学优化 Mathematical Optimization
- 概率和统计 Probability and statistics
- 排队论 Queueing theory
- 社交网络/交通预测模型 Social network/traffic prediction modeling
- 随机过程 Stochastic processes
- 供应链管理 Supply chain management
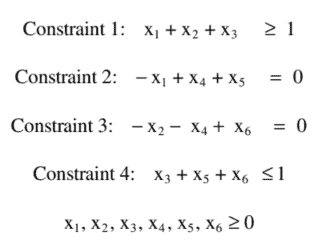
运筹学代写
数学代写|运筹学作业代写OPERATIONS RESEARCH代考|deGeneRaCy
First, the other row (unselected row) would change in similar fashion as the ratio of selected row. In all possibilities, the ratio value would be either zero or undefined, making unselected row degenerate. Second, if optimal solution is reached at this iteration, then the final solution is reported. However, if there are subsequent iterations and a degenerate row is selected as outgoing variable in any of those iterations, then there is always the risk that the solution will enter a loop of coming in and out of degeneracy without affecting the objective function. Degeneracy does not indicate faulty model formulation. But care should be taken during the solving process to avoid repeating the same sequence of iterations without practically affecting the objective function.
The following illustration explains the concept clearly:
Minimize $2 \mathrm{x}{1}+8 \mathrm{x}{2}+9 \mathrm{x}{3}+4 \mathrm{x}{4}+7 \mathrm{x}{5}+3 \mathrm{x}{6}$
Subject to:
Constraint 1: $\quad \mathrm{x}{1}+\mathrm{x}{2}+\mathrm{x}{3} \geq 1$ Constraint 2: $-\mathrm{x}{1}+\mathrm{x}{4}+\mathrm{x}{5}=0$
Constraint 3: $-\mathrm{x}{2}-\mathrm{x}{4}+\mathrm{x}{6}=0$ Constraint 4: $\quad \mathrm{x}{3}+\mathrm{x}{5}+\mathrm{x}{6} \leq 1$
$$
\mathrm{x}{1}, \mathrm{x}{2}, \mathrm{x}{3}, \mathrm{x}{4}, \mathrm{x}{5}, \mathrm{x}{6} \geq 0
$$
数学代写|运筹学作业代写OPERATIONS RESEARCH代考|unbounded
A solution is termed as unbounded when objective function $\mathrm{Z}$ can be changed, i.e. increased in the case of maximization to positive infinity level and decreased in the case of minimization to negative infinity level. This implies that considered constraints in solution are unable to bind the change in Z. Ideally, every firm would want to have infinite profits, but practically it is not possible, so an unbounded solution would infer erroneous formulation of constraints. In other words, an unbounded solution can be explained as a solution when an outgoing variable cannot be selected because of negative or undefined ratio values. This happens when the incoming variable with a maximum positive value is selected but the coefficients in pivot column are either zero or negative.
This is illustrated by the following example:
Maximize $\mathrm{Z}=120 \mathrm{x}{1}+180 \mathrm{x}{2}$
Subject to:
10×1 2 + 20x ≤ 1,000
1×1 2 + 1x ≤ 350
数学代写|运筹学作业代写OPERATIONS RESEARCH代考|infeasibility
When no solution can fulfil all the constraints simultaneously, then solution is considered to be infeasible. It is important to note that infeasibility does not imply wrong formulation of linear programming model. On the other hand, it helps managers to improve solutions by concentrating on constraints which are binding for fulfilment of conditions of other constraints. There are two indications which help to judge the infeasibility of a solution. First, as suggested, when conditions of all constraints whether greater or less than are not met simultaneously and second, when an artificial variable remains in the final solution and is positive. Artificial variable by nature does not contribute in any fashion to objective function, so they should be removed from solution at the earliest possible. If that does not happen, it results in infeasibility. Also, artificial variables are required only to resolve greater than or equal to
constraints. Thus, as a problem with less than or equal to inequality does not include artificial variable, so it does not suffer from the condition of infeasibility pertaining to artificial variables.
Illustration of infeasibility is provided below.
0x1 2 + 1x + 1×3 ≥ 2
−1×1 2 + 1x + 1×3 1 ≥
0x1 2 + 0x 1 − ≥ x 3 1
x1 2 ,x ,x3 0
运筹学代考
数学代写|运筹学作业代写OPERATIONS RESEARCH代考|DEGENERACY
首先,另一排你ns和一世和C吨和dr○在将以与所选行的比率类似的方式变化。在所有可能性中,比率值要么为零,要么未定义,从而使未选择的行退化。其次,如果在本次迭代中达到最优解,则报告最终解。但是,如果有后续迭代并且在任何这些迭代中选择退化行作为传出变量,则始终存在解决方案将进入进入和退出退化循环而不影响目标函数的风险。退化并不表示错误的模型制定。但在求解过程中应注意避免重复相同的迭代序列而不实际影响目标函数。
下图清楚地解释了这个概念:
Constraint 1: x +1 2 x + x 3 ≥ 1
Constraint 2: − = x +1 4 x + x 0 5
Constraint 3: − − x x 246 + = x 0
Constraint 4: x +356 x + x 1 ≤
x1, x234 ,x ,x ,x5 6 , x ≥ 0
数学代写|运筹学作业代写OPERATIONS RESEARCH代考|UNBOUNDED
当目标函数时,解决方案称为无界和可以改变,即在最大化到正无穷大的情况下增加,在最小化到负无穷大的情况下减小。这意味着解决方案中考虑的约束无法约束 Z 的变化。理想情况下,每个公司都希望获得无限利润,但实际上这是不可能的,因此无界解决方案会推断出错误的约束公式。换句话说,当由于负值或未定义的比率值而无法选择传出变量时,可以将无界解决方案解释为解决方案。This happens when the incoming variable with a maximum positive value is selected but the coefficients in pivot column are either zero or negative.
下面的例子说明了这一点:
最大化 $\mathrm{Z}=120 \mathrm{x} {1}+180 \mathrm{x} {2}$
服从:
10×1 2 + 20x ≤ 1,000
1×1 2 + 1x ≤ 350
数学代写|运筹学作业代写OPERATIONS RESEARCH代考|INFEASIBILITY
当没有解决方案可以同时满足所有约束时,则认为解决方案是不可行的。需要注意的是,不可行并不意味着线性规划模型的错误表述。另一方面,它帮助管理者通过关注约束来改进解决方案,这些约束对满足其他约束条件具有约束力。有两个迹象有助于判断解决方案的不可行性。首先,如建议的那样,当所有约束条件(无论大于或小于)没有同时满足时,其次,当人工变量保留在最终解中并且为正时。人工变量本质上对目标函数没有任何贡献,因此应尽早将它们从解决方案中删除。如果不这样做,就会导致不可行。
约束。因此,由于小于或等于不等式的问题不包括人为变量,所以它不存在与人为变量有关的不可行条件。
下面提供了不可行的说明。
0x1 2 + 1x + 1×3 ≥ 2
−1×1 2 + 1x + 1×3 1 ≥
0x1 2 + 0x 1 − ≥ x 3 1
x1 2 ,x ,x3 0