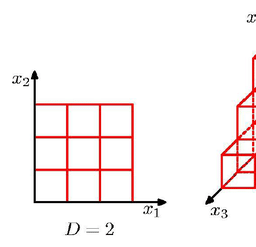
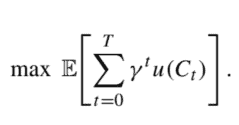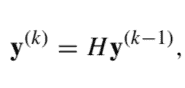如果你也在为遇到的matlab相关的难题发愁,请随时右上角联系我们的24/7代写客服。MATLAB®将为迭代分析和设计过程而调整的桌面环境与直接表达矩阵和阵列数学的编程语言相结合。它包括用于创建脚本的实时编辑器,这些脚本将代码、输出和格式化文本结合在可执行的笔记本中。
- 专业构建
MATLAB工具箱是专业开发的,经过严格的测试,并有完整的文件记录。 - 拥有互动式应用程序
MATLAB应用程序让您看到不同的算法是如何与您的数据一起工作的。迭代直到您得到您想要的结果,然后自动生成一个MATLAB程序来重现或自动完成您的工作。 - 以及扩展的能力
只需稍加修改代码,就可以将您的分析扩展到集群、GPU和云上运行。不需要重写你的代码或学习大数据编程和内存外技术。
my-assignmentexpert™ matlab作业代写,免费提交作业要求, 满意后付款,成绩80\%以下全额退款,安全省心无顾虑。专业硕 博写手团队,所有订单可靠准时,保证 100% 原创。my-assignmentexpert™, 最高质量的matlab作业代写作业代写,服务覆盖北美、欧洲、澳洲等 国家。 在代写价格方面,考虑到同学们的经济条件,在保障代写质量的前提下,我们为客户提供最合理的价格。 由于统计Statistics作业种类很多,同时其中的大部分作业在字数上都没有具体要求,因此matlab作业代写作业代写的价格不固定。通常在matlab专家查看完作业要求之后会给出报价。作业难度和截止日期对价格也有很大的影响。
想知道您作业确定的价格吗? 免费下单以相关学科的专家能了解具体的要求之后在1-3个小时就提出价格。专家的 报价比上列的价格能便宜好几倍。
my-assignmentexpert™ 为您的留学生涯保驾护航 在matlab作业代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的应用数学applied math代写服务。我们的专家在matlab作业代写方面经验极为丰富,各种matlab作业代写相关的作业也就用不着 说。
我们提供的matlab作业代写及其相关学科的代写,服务范围广, 其中包括但不限于:
- 数据分析
- 数值与符号计算
- 工程与科学绘图
- 控制系统设计
- 航天工业
- 汽车工业
- 生物医学工程
- 语音处理
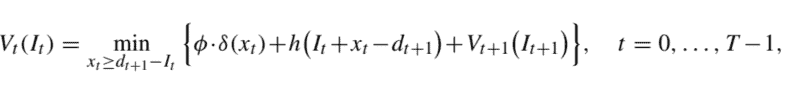
运筹学代写
数学代写|matlab作业代写|Using Shortest Paths to Solve the Deterministic Lot-Sizing Problem
Let us consider a simple version of deterministic lot-sizing, whereby we only deal with fixed ordering charges $\phi$ and inventory holding cost $h$. Demand $d_{t}$, $t=1, \ldots, T$, is deterministic. Without loss of generality, we may assume that both initial and terminal inventories are zero. If initial inventory is $I_{0}>0$, we may simply subtract it from the initial demand (a procedure called demand netting). If we wish to set a target terminal inventory $I_{T}>0$, we may just add it to demand $d_{T}$ in the last time interval. Let us assume, for the sake of convenience, that demand is nonzero in the first time period (otherwise, we just shift time forward). If we want to keep inventory to a minimum, we should just order what is needed in each time bucket, setting $x_{t}=d_{t+1}$, for $t=0, \ldots, T-1$. If we want to keep fixed charges to a minimum, we should order once:
$$
x_{0}=\sum_{t=1}^{T} d_{t}
$$
Quite likely, neither approach is optimal, since we want to minimize the sum of both inventory and ordering costs, and we must find a compromise solution. In principle, we may solve the problem by the following DP recursion:
$$
V_{t}\left(I_{t}\right)=\min {x{t} \geq d_{t+1}-I_{t}}\left{\phi \cdot \delta\left(x_{t}\right)+h\left(I_{t}+x_{t}-d_{t+1}\right)+V_{t+1}\left(I_{t+1}\right)\right}, \quad t=0, \ldots, T-1
$$
数学代写|MATLAB作业代写|Stochastic Lot-Sizing: S and (s, S) Policies
The Wagner-Whitin condition provides us with an efficient approach to solve a deterministic and uncapacitated lot-sizing problem. It is natural to ask whether we
are so lucky in the stochastic case. The answer is negative, but not completely negative. To begin with, in a stochastic case, we must deal with the unpleasing possibility of failing to meet demand. Let us assume that customers are patient and willing to wait, so that there is no lost sales penalty, and that the total cost function includes a term like
$$
q(s)=h \max {0, s}+b \max {0,-s}
$$
where $s$ is a state variable, the inventory level, which may be positive (on-hand inventory) or negative (backlog); $h$ is the usual inventory holding cost, and $b>h$ is a backlog cost. Note that $q(\cdot)$ is a convex penalty and goes to $+\infty$ when $s \rightarrow \pm \infty$. For now, we disregard fixed charges, but we also include a linear variable cost, with unit ordering cost $c$. Hence, the overall problem requires to find a policy minimizing the expected total cost over $T$ time periods:
$$
\mathbb{E}{0}\left[\sum{t=0}^{T-1}\left{c x_{t}+q\left(I_{t}+x_{t}-d_{t+1}\right)\right}\right]
$$
where $x_{t}$ is the amount ordered and immediately received at time $t$, as before.
We may write the DP recursion as
$$
V_{t}\left(I_{t}\right)=\min {x{t} \geq 0}\left{c x_{t}+H\left(I_{t}+x_{t}\right)+\mathbb{E}\left[V_{t+1}\left(I_{t}+x_{t}-d_{t+1}\right)\right]\right}
$$
where we define
$$
H\left(y_{t}\right) \doteq \mathbb{E}\left[q\left(y_{t}-d_{t+1}\right)\right]=h \mathbb{E}\left[\max \left{0, y_{t}-d_{t+1}\right}\right]+b \mathbb{E}\left[\max \left{0, d_{t+1}-y_{t}\right}\right]
$$
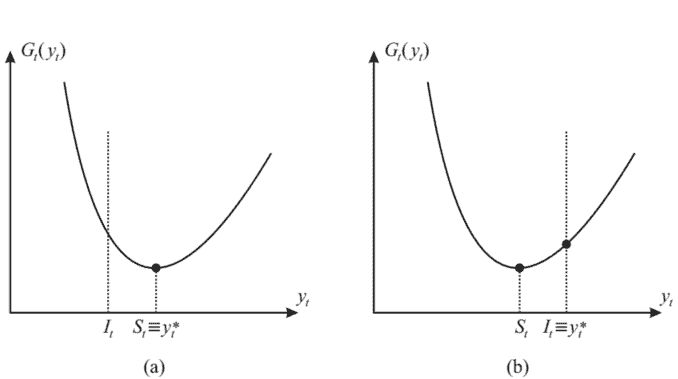
数学代写|MATLAB作业代写|Structural Properties of Value Functions
Given the role that convexity plays in proving optimality of base-stock policies for inventory control, we may ask under which conditions we may prove useful structural properties of the value function, like continuity, differentiability, monotonicity, as well as convexity/concavity. When the action space is discrete and small, convexity/concavity is irrelevant, since each optimization subproblem can be solved by enumeration. However, in a more challenging problem with continuous actions, we may wonder if we can use standard local optimization methods from nonlinear programming, or we should apply demanding global optimization algorithms.
Unfortunately, the issue is quite complicated. There are some rather technical results, but quite often the matter must be assessed case by case. We just want to stress here that, even if we are able to prove nice properties of a value function, these may be lost when resorting to an approximate or compact representation of the value function. Even the learning algorithm itself, like those used to fit neural networks, may fail to ensure global optimality. Hence, we should always run a careful empirical analysis of performance of any numerical solution strategy we come up with. Again, this tends to be quite problem dependent, and we will not consider the matter in this book.
matlab代写
数学代写|MATLAB作业代写|USING SHORTEST PATHS TO SOLVE THE DETERMINISTIC LOT-SIZING PROBLEM
让我们考虑一个简单版本的确定性批量,我们只处理固定的订购费用φ和库存持有成本H. 要求d吨,吨=1,…,吨, 是确定性的。不失一般性,我们可以假设初始库存和最终库存都为零。如果初始库存是一世0>0,我们可以简单地从初始需求中减去它一种pr○C和d你r和C一种一世一世和dd和米一种ndn和吨吨一世nG. 如果我们希望设置目标终端库存一世吨>0,我们可以将其添加到需求中d吨在最后的时间间隔内。为方便起见,我们假设第一个时间段的需求不为零○吨H和r在一世s和,在和j你s吨sH一世F吨吨一世米和F○r在一种rd. 如果我们想将库存保持在最低限度,我们应该只在每个时间桶中订购需要的东西,设置X吨=d吨+1, 为了吨=0,…,吨−1. 如果我们想将固定费用保持在最低限度,我们应该订购一次:
X0=∑吨=1吨d吨
很可能,这两种方法都不是最优的,因为我们希望最小化库存和订购成本的总和,我们必须找到一个折中的解决方案。原则上,我们可以通过以下 DP 递归来解决这个问题:
$$
V_{t}\left对的对的=\min {x {t} \geq d_{t+1}-I_{t}}\left{\phi \cdot \delta\leftx_{t}\右x_{t}\右+h\左I_{t}+x_{t}-d_{t+1}\rightI_{t}+x_{t}-d_{t+1}\right+V_{t+1}\左我_{t+1}\对我_{t+1}\对\right}, \quad t=0, \ldots, T-1
$$
数学代写|MATLAB作业代写|STOCHASTIC LOT-SIZING: S AND (S, S) POLICIES
Wagner-Whitin 条件为我们提供了一种有效的方法来解决确定性和无容量批量问题。很自然地问我们是否
在随机情况下是如此幸运。答案是否定的,但并非完全否定。首先,在随机情况下,我们必须处理无法满足需求的令人不快的可能性。让我们假设客户有耐心并愿意等待,因此不会有损失的销售损失,并且总成本函数包括一个
q(s)=H最大限度0,s+b最大限度0,−s
在哪里s是一个状态变量,库存水平,可能为正○n−H一种nd一世nv和n吨○r和或否定b一种C到一世○G;H是通常的库存持有成本,并且b>H是积压成本。注意q(⋅)是一个凸惩罚并且去+∞什么时候s→±∞. 目前,我们不考虑固定费用,但我们还包括线性可变成本,即单位订购成本C. 因此,整个问题需要找到一个策略来最小化预期总成本吨时间段:
$$
\mathbb{E}{0}\left[\sum{t=0}^{T-1}\left{c x_{t}+q\left(I_{t}+x_{t}-d_{t+1}\right)\right}\right]
$$
where $x_{t}$ is the amount ordered and immediately received at time $t$, as before. We may write the DP recursion as
$$
V_{t}\left(I_{t}\right)=\min {x{t} \geq 0}\left{c x_{t}+H\left(I_{t}+x_{t}\right)+\mathbb{E}\left[V_{t+1}\left(I_{t}+x_{t}-d_{t+1}\right)\right]\right}
$$
where we define
$$
H\left(y_{t}\right) \doteq \mathbb{E}\left[q\left(y_{t}-d_{t+1}\right)\right]=h \mathbb{E}\left[\max \left{0, y_{t}-d_{t+1}\right}\right]+b \mathbb{E}\left[\max \left{0, d_{t+1}-y_{t}\right}\right]
$$
数学代写|MATLAB作业代写|STRUCTURAL PROPERTIES OF VALUE FUNCTIONS
鉴于凸性在证明库存控制的基本库存政策的最优性中所起的作用,我们可能会问,在哪些条件下,我们可以证明价值函数的有用结构特性,如连续性、可微性、单调性以及凸/凹。当动作空间离散且较小时,凸度/凹度无关紧要,因为每个优化子问题都可以通过枚举来解决。然而,在具有连续动作的更具挑战性的问题中,我们可能想知道是否可以使用非线性规划的标准局部优化方法,或者我们应该应用要求苛刻的全局优化算法。
不幸的是,这个问题相当复杂。有一些相当技术性的结果,但通常必须逐案评估此事。我们只是想在这里强调一点,即使我们能够证明价值函数的良好性质,当诉诸价值函数的近似或紧凑表示时,这些性质也可能会丢失。即使是学习算法本身,比如那些用于拟合神经网络的算法,也可能无法确保全局最优性。因此,我们应该始终对我们提出的任何数值求解策略的性能进行仔细的实证分析。同样,这往往是相当依赖于问题的,我们不会在本书中考虑这个问题。

统计代考
统计是汉语中的“统计”原有合计或汇总计算的意思。 英语中的“统计”(Statistics)一词来源于拉丁语status,是指各种现象的状态或状况。
数论代考
数论(number theory ),是纯粹数学的分支之一,主要研究整数的性质。 整数可以是方程式的解(丢番图方程)。 有些解析函数(像黎曼ζ函数)中包括了一些整数、质数的性质,透过这些函数也可以了解一些数论的问题。 透过数论也可以建立实数和有理数之间的关系,并且用有理数来逼近实数(丢番图逼近)
数值分析代考
数值分析NumericalAnalysis,又名“计算方法”,是研究分析用计算机求解数学计算问题的数值计算方法及其理论的学科。 它以数字计算机求解数学问题的理论和方法为研究对象,为计算数学的主体部分。
随机过程代写
随机过程,是依赖于参数的一组随机变量的全体,参数通常是时间。 随机变量是随机现象的数量表现,其取值随着偶然因素的影响而改变。 例如,某商店在从时间t0到时间tK这段时间内接待顾客的人数,就是依赖于时间t的一组随机变量,即随机过程
MATLAB代写
MATLAB 是一种用于技术计算的高性能语言。它将计算、可视化和编程集成在一个易于使用的环境中,其中问题和解决方案以熟悉的数学符号表示。典型用途包括:数学和计算算法开发建模、仿真和原型制作数据分析、探索和可视化科学和工程图形应用程序开发,包括图形用户界面构建MATLAB 是一个交互式系统,其基本数据元素是一个不需要维度的数组。这使您可以解决许多技术计算问题,尤其是那些具有矩阵和向量公式的问题,而只需用 C 或 Fortran 等标量非交互式语言编写程序所需的时间的一小部分。MATLAB 名称代表矩阵实验室。MATLAB 最初的编写目的是提供对由 LINPACK 和 EISPACK 项目开发的矩阵软件的轻松访问,这两个项目共同代表了矩阵计算软件的最新技术。MATLAB 经过多年的发展,得到了许多用户的投入。在大学环境中,它是数学、工程和科学入门和高级课程的标准教学工具。在工业领域,MATLAB 是高效研究、开发和分析的首选工具。MATLAB 具有一系列称为工具箱的特定于应用程序的解决方案。对于大多数 MATLAB 用户来说非常重要,工具箱允许您学习和应用专业技术。工具箱是 MATLAB 函数(M 文件)的综合集合,可扩展 MATLAB 环境以解决特定类别的问题。可用工具箱的领域包括信号处理、控制系统、神经网络、模糊逻辑、小波、仿真等。