数学代写| Problems with No Solution or Infinitely Many Solutions 凸优化代考
凸优化代写
The discussion in Section $3.3$ made it clear that it is possible for a linear programming problem to have infinitely many solutions. But it is also possible that there is no solution if the feasible region is empty or unbounded. Suppose that a linear programming problem has two distinct solution points $P$ and $Q$. Then the level objective line (or plane or hyperplane) through $P$ contains $Q$ since they both have the same value of the objective function. Consider the line segment $P Q$ joining $P$ to $Q$. This segment lies entirely within that level objective line (or plane, etc.), so every point on that segment has the same value of the objective function as $P$ and $Q .$ But since the feasible set $X$ is convex by Theorem 3.8, Part 1, every one of the points on this segment is feasible. The conclusion is that if $P$ and $Q$ are optimal, so is every point on $P Q$, so there are actually infinitely many solutions.
We have just shown that, like the systems of linear equations in Chapter 1, there are exactly three possibilities for a linear programming problem: there is no solution, a unique solution, or infinitely many solutions. We’ve seen examples of the case of a unique solution (the lemonade stand problem and the used car problem both had unique solutions). In this section, we give examples of the other two cases.
$3.4$ Problems with No So
125
empty feasible set.
Example 3.9 A problem with an empty feasible set. Maximize: $w=10 x+3 y+6 z$
subject to:
$$
\begin{aligned}
&2 x+3 y+5 z \leq 150 \
&2 x+3 y+5 z \geq 225 \
&x \geq 0, y \geq 0, z \geq 0
\end{aligned}
$$
Example 3.10 A problem with unbounded feasible set and no solution. $$ \begin{array}{l}\text { Maximize: } P=2 x+y \ \text { subject to: } \ y \leq 10 \ x+y \geq 5 \ x \geq 0, y \geq 0\end{array} $$
Clearly, no point $P=(x, y, z)$ can have the property that $2 x+3 y+5 z$ is less than or equal to 150 for different values of $c$, are parallel planes in space. The solution set to the first inequality is the half-space containing the origin, of the plane closer to the origin. The solution set to the second inequality is the half-space not containing the origin, of the plane farther from the origin. There is no intersection of these half-spaces because their boundary planes are parallel. Thus, there are no feasible points.
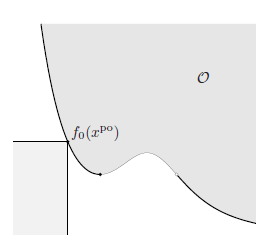
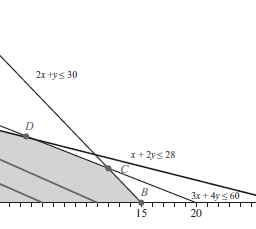
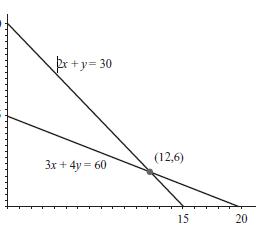
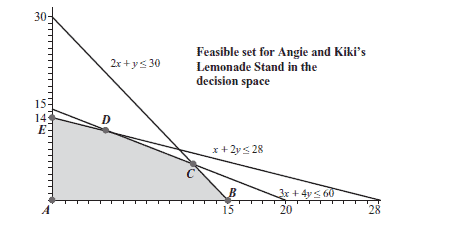
Figure $3.8$ shows a graph of the feasible region in the decision space.
Figure $3.8$ An unbounded feasible set.
This region is unbounded in the positive $x$ direction. In particular, points of the form $(x, 0)$ are all feasible if $x \geq 5$. The value of the objective function at $(x, 0)$ is $2 x$. Since $x$ can be chosen arbitrarily large, we see the objective function becomes arbitrarily large also. $P$ grows without bound as you move to the right. Thus, there is no maximum point, and the problem has no solution. On the other hand, if the problem had been to minimize $P$, a solution would exist, which can be easily seen by plotting a few level objective lines. According to the algorithm in Section $3.2$ (or determined by viewing the level objective lines), the solution would be one of the three corners
凸优化代考
第 3.3 节中的讨论清楚地表明,线性规划问题可能有无限多个解。但如果可行域为空或无界,也有可能没有解。假设一个线性规划问题有两个不同的解点 $P$ 和 $Q$。然后通过 $P$ 的水平目标线(或平面或超平面)包含 $Q$,因为它们都具有相同的目标函数值。考虑将 $P$ 连接到 $Q$ 的线段 $P Q$。该段完全位于该水平目标线(或平面等)内,因此该段上的每个点都具有与 $P$ 和 $Q 相同的目标函数值。但是由于可行集 $X$ 是凸的根据定理 3.8,第 1 部分,该段上的每个点都是可行的。结论是,如果 $P$ 和 $Q$ 是最优的,那么 $P Q$ 上的每个点也是最优的,所以实际上有无穷多个解。
我们刚刚表明,就像第 1 章中的线性方程组一样,线性规划问题恰好存在三种可能性:无解、唯一解或无限多个解。我们已经看到了独特解决方案的例子(柠檬水摊问题和二手车问题都有独特的解决方案)。在本节中,我们将举例说明其他两种情况。
$3.4$ 不存在的问题
125
空可行集。
例 3.9 一个空可行集的问题。最大化:$w=10 x+3 y+6 z$
受制于:
$$
\开始{对齐}
&2 x+3 y+5 z \leq 150 \
&2 x+3 y+5 z \geq 225 \
&x \geq 0, y \geq 0, z \geq 0
\end{对齐}
$$
例 3.10 一个有无限可行集且无解的问题。 $$ \begin{array}{l}\text { 最大化: } P=2 x+y \ \text { 服从: } \ y \leq 10 \ x+y \geq 5 \ x \geq 0, y \geq 0\end{数组} $$
显然,对于不同的 $c$ 值,$P=(x, y, z)$ 不能具有 $2 x+3 y+5 z$ 小于或等于 150 的性质,它们是空间中的平行平面。设置为第一个不等式的解决方案是包含原点的半空间,靠近原点的平面。第二个不等式的解是不包含原点的半空间,即离原点较远的平面。这些半空间没有相交,因为它们的边界平面是平行的。因此,没有可行的点。
图$3.8$ 显示了决策空间中的可行区域图。
图 $3.8$ 一个无界可行集。
该区域在正 $x$ 方向上是无界的。特别是,如果 $x \geq 5$,$(x, 0)$ 形式的点都是可行的。 $(x, 0)$ 处的目标函数值为 $2 x$。由于 $x$ 可以选择任意大,我们看到目标函数也变得任意大。当您向右移动时,$P$ 会无限增长。因此,没有最大值,问题也没有解决方案。另一方面,如果问题是最小化 $P$,则存在解决方案,通过绘制几条水平目标线可以很容易地看出这一点。根据 $3.2$ 中的算法(或通过查看水平目标线确定),解决方案将是三个角之一

数学代写| Chebyshev polynomials 数值分析代考 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。
时间序列分析代写
统计作业代写
随机过程代写
随机过程,是依赖于参数的一组随机变量的全体,参数通常是时间。 随机变量是随机现象的数量表现,其取值随着偶然因素的影响而改变。 例如,某商店在从时间t0到时间tK这段时间内接待顾客的人数,就是依赖于时间t的一组随机变量,即随机过程