数学代写| Introduction and Graphical Solutions 凸优化代考
凸优化代写
Linear programming problems are special cases of optimization problems. There is an objective function whose values change according to the values of input variables called decision variables. The goal is to choose the values of the decision variables that will produce the optimal value of the objective function. “Optimal” means either the largest possible value (this is called a maximization problem) or the smallest possible value (this is called a minimization problem.)
One is usually not free to specify just any values of the decision variables; typically there are constraints that limit the choices. What distinguishes a linear programming problem from a general constrained optimization problem is that both the constraints and the objective function are determined by linear equations; that is, the decision variables appear only to the first power in these equations. In practice, the constraints often arise from a limited supply of resources, so linear programming can be viewed as a tool to determine the best way to allocate scarce resources. However, we are getting ahead of ourselves. In this section, we present a very simplified scenario that shows how a linear programming problem might arise naturally. We begin with a simple algebra problem of the type we have seen in Chapter 1 .
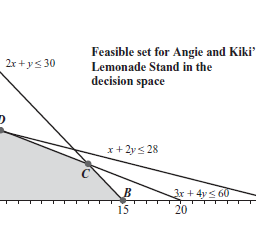
Example 3.1 Angie and Kiki’s Lemonade Stand. Angie and her sister Kiki want to set up a roadside lemonade stand in order to save money for college. They sell two types of lemonade: a glass of sweet lemonade uses three lemons and 2 tablespoons of sugar, and it sells for $\$ 1.25 .$ A glass of tart lemonade uses four lemons and 1 tablespoon of sugar, and it sells for $\$ 1.50$. How many glasses of each type should be mixed if their mother has given them 60 lemons and 30 tablespoons of sugar to use?
In solving a problem like this, we make some simplifying assumptions, such as assuming the children can sell all of the lemonade they make. We also assume that the other ingredients (water, ice, cups, etc.) are in unlimited supply, so the only constraints come from the limited amounts of lemons and sugar. We can model this as a system of linear equations. Let $x$ stand for the number of glasses of sweet lemonade and $y$ stand for the number of glasses of tart lemonade.
We can now obtain an equation (i.e., a constraint) from each limited resource, just as we did with the bongo drum example in Chapter 2:
$$
\begin{aligned}
3 x+4 y &=60 \text { (lemons) } \
x+2 y &=30 \text { (tablespoons sugar) }
\end{aligned}
$$
We recognize this as a system of two linear equations in two unknowns, and we have several
We recognize this as a system of two linear equations in two methods at our disposal to solve it. (Before solving it, think for a moment and see if you can spot another, unstated assumption that we made in setting up this system. We’ll come back to this point in Chapter 2 . The matrix form of the system is
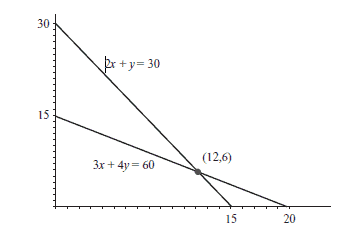
The inverse of the coefficient matrix is Therefore the solution is $\left[\begin{array}{cc}3 & 4 \ 2 & 1\end{array}\right]\left[\begin{array}{l}x \ y\end{array}\right]=\left[\begin{array}{l}60 \ 30\end{array}\right] \cdot$ $$ \left[\begin{array}{l}x \ y\end{array}\right]=-\frac{1}{5}\left[\begin{array}{cc}1 & -4 \ -2 & 3\end{array}\right] \cdot-2 $$ That is, the solution is $(x, y)=(12,6)$, so our heroines should mix 12 glasses of sweet lemonade and six glasses of tart lemonade. The reader may have noticed that we did not use the prices at all in finding the solution to the system, but if you want to know the total revenue $R$ earned from selling the lemonade, it is given by $$ R=1.25 x+1.5 y=1.25(12)+1.5(6)=\$ 24, $$
103 Of course, one may also find the solution by substitution, elimination, or even by graphing it, as shown in Figure $3.1$.
凸优化代考
线性规划问题是优化问题的特例。有一个目标函数,其值根据称为决策变量的输入变量的值而变化。目标是选择将产生目标函数的最佳值的决策变量的值。 “最优”是指最大可能值(这称为最大化问题)或最小可能值(这称为最小化问题)。
通常不能随意指定决策变量的任何值;通常存在限制选择的约束。线性规划问题与一般约束优化问题的区别在于约束和目标函数都由线性方程确定;也就是说,决策变量在这些方程中只出现一次方。在实践中,约束通常来自资源的有限供应,因此线性规划可以被视为确定分配稀缺资源的最佳方式的工具。然而,我们正在超越自己。在本节中,我们展示了一个非常简化的场景,展示了线性规划问题是如何自然产生的。我们从一个我们在第 1 章中看到的类型的简单代数问题开始。
示例 3.1 Angie 和 Kiki 的柠檬水摊。安吉和她的妹妹琪琪想在路边设立一个柠檬水摊,以节省上大学的钱。他们卖两种柠檬水:一杯甜柠檬水使用三个柠檬和 2 汤匙糖,售价为 $\$ 1.25 .$ 一杯酸柠檬水使用四个柠檬和 1 汤匙糖,售价 $\$ \$ 1.50 美元。如果他们的母亲给了他们 60 个柠檬和 30 汤匙糖,每种类型应该混合多少杯?
在解决这样的问题时,我们做了一些简化的假设,例如假设孩子们可以卖掉他们制作的所有柠檬水。我们还假设其他成分(水、冰、杯子等)是无限供应的,所以唯一的限制来自柠檬和糖的数量有限。我们可以将其建模为线性方程组。令 $x$ 代表甜柠檬水的杯数,$y$ 代表酸柠檬水的杯数。
我们现在可以从每个有限的资源中获得一个方程(即一个约束),就像我们在第 2 章中处理邦戈鼓的例子一样:
$$
\开始{对齐}
3 x+4 y &=60 \text { (柠檬) } \
x+2 y &=30 \text {(汤匙糖)}
\end{对齐}
$$
我们认为这是一个有两个未知数的两个线性方程组,我们有几个
我们认为这是一个由两个线性方程组成的系统,我们可以使用两种方法来解决它。 (在解决它之前,想一想,看看你是否能发现我们在建立这个系统时所做的另一个未说明的假设。我们将在第 2 章回到这一点。系统的矩阵形式是
系数矩阵的逆是 因此解是 $\left[\begin{array}{cc}3 & 4 \ 2 & 1\end{array}\right]\left[\begin{array}{l} x \ y\end{array}\right]=\left[\begin{array}{l}60 \ 30\end{array}\right] \cdot$ $$ \left[\begin{array}{ l}x \ y\end{array}\right]=-\frac{1}{5}\left[\begin{array}{cc}1 & -4 \ -2 & 3\end{array} \right] \cdot-2 $$ 即解是$(x, y)=(12,6)$,所以我们的女主角应该混合12杯甜柠檬水和6杯酸柠檬水。读者可能已经注意到,我们在寻找系统的解决方案时根本没有使用价格,但是如果您想知道销售柠檬水所获得的总收入 $R$,它由 $$ R=1.25 x 给出+1.5 y=1.25(12)+1.5(6)=\$ 24, $$
103 当然,人们也可以通过替换、消除,甚至通过绘图来找到解决方案,如图 $3.1$ 所示。

数学代写| Chebyshev polynomials 数值分析代考 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。
时间序列分析代写
统计作业代写
随机过程代写
随机过程,是依赖于参数的一组随机变量的全体,参数通常是时间。 随机变量是随机现象的数量表现,其取值随着偶然因素的影响而改变。 例如,某商店在从时间t0到时间tK这段时间内接待顾客的人数,就是依赖于时间t的一组随机变量,即随机过程